
- •Глава 3. Поляризационные эффекты при взаимодействии релятивистских частиц с плоской электромагнитной волной
- •10. Спонтанное излучение релятивистского электрона в поле плоской электромагнитной волны
- •10.1 Волновые функции и квантовые числа электрона
- •10.2 Вероятность спонтанного излучения поляризованного электрона
- •11. Само поляризация спина электрона в поле плоской электромагнитной волны.
- •11.1. Максимальная самополяризация электрона в плоской волне.
- •11.2 Анализ поведения электронного спина
- •12. Нелинейные эффекты в процессе взаимодействия плоской электромагнитной волны с электроном.
- •12.1 Модель квантовой электродинамики "электрон плюс квантованное поле плоской электромагнитной волны"
11. Само поляризация спина электрона в поле плоской электромагнитной волны.
Эффект само поляризации спина электрона является одним из наиболее интересных эффектов при квантовомеханическом описании процесса спонтанного излучения релятивистских электронов во внешних электромагнитных полях. Это явление проявляется в том, что в ансамбле частиц устанавливается преимущественная ориентация спина в результате встрясок, испытываемых электроном со стороны испускаемых фотонов.
Впервые задача о принципиальной возможности использования комптоновского рассеяния для получения поляризованных электронов была поставлена в [192, 193], где были исследованы особенности поведения сечения рассеяния в зависимости от спина электронов. Однако рекомендации из [192, 193] пока практически не реализованы, этому можно дать такое объяснение: если поместить на время порядка одного часа в накопительное кольцо с мощным магнитным полем пучок электронов, то из-за эффекта радиационной само поляризации при синхротронном излучении, впервые предсказанного в [194, 195] и детально исследованного в работах [1, 12, 196-201] устанавливается преимущественная ориентация электронного спина против направления магнитного поля. Это, пожалуй, единственный способ получения релятивистских поляризованных электронов известный в настоящее время. Здесь направление в пространстве, по которому ориентируется спин электрона, не связано с динамикой электрона.
Затем такой пучок поляризованных релятивистских электронов можно использовать в физических экспериментах, выводя его из накопителя.
Основные выводы этой теории получили экспериментальное подтверждение [203-208].
Авторы работ [209, 210] сделали вывод, что при плоскостном каналировании электронов в изогнутых монокристаллах должна наблюдаться само поляризация спина электрона. Аналогичный вывод был сделан в [211, 212] относительно аксиального каналирования электронов в кристалле. Это связано с тем, что характер движения электрона в вышеприведенных случаях в общих чертах совпадает с движением в магнитном поле.
Другой подход необходим в случае поля плоской электромагнитной волны. Дело в том что если направление спина в пространстве и времени фиксировано, то в среднем преимущественной ориентации спина не происходит, как это проанализировано при комптон-эффекте в [109], причем в этой работе вектор спина выбирался направленным по направлению распространения плоской волны. Очень важным при решении проблемы преимущественной ориентации спина является правильный выбор ориентации векторов спина.
В работах [182, 183, 192, 193] изучалось дифференциальное сечение, которое в сильной степени зависит от вектора электронного спина, но после интегрирования по углам вылета фотона [109] в полном сечении эта зависимость исчезает (в членах, связанных с переориентацией спина). Но необходима уточнить результат работы [109] тем, что вектор спина не только является фиксированным, но и не связан с характеристиками электрона в конечном состоянии, только тогда результат [109] верен.
Оказывается, существуют направления, связанные с динамикой самого электрона, вдоль которых может наблюдаться преимущественная ориентация пучка электронов. Найдем эти направления.
Для этого из (3.27) суммируя по конечным и усредняя по начальным спинам, получим известную [109, 184-189] полную вероятность излучения неполяризованного электрона. Чтобы получить формулу для этой полной вероятности, достаточно подставить в (3.27) следующие выражения
![]() , (3.30)
, (3.30)
![]()
Исследуем
эффект радиационной самополяризации
в плоской электромагнитной волне подобно
тому, как это сделано в случае эффекта
самополяризации в магнитном поле
[194-203], то есть примем в рассмотрении
вероятности переходов только с переворотом
спина
![]() ,
поскольку первоначальное соотношение
числа частиц, имеющих разную ориентацию
спина, переходы без переориентации
спина не изменяют.
,
поскольку первоначальное соотношение
числа частиц, имеющих разную ориентацию
спина, переходы без переориентации
спина не изменяют.
Для
того, чтобы изучить эффект самополяризации
спина электрона, надо использовать
кинетическое уравнение [194, 195], так как
этот процесс имеет релаксационный
характер. После того, как пройдет время
![]() ,
где
,
где![]() - время релаксации, в системе устанавливается
динамическое равновесие.
- время релаксации, в системе устанавливается
динамическое равновесие.
Пусть
![]() - равновесная доля электронов со спином
- равновесная доля электронов со спином![]() в конечном состоянии, а
в конечном состоянии, а![]() - равновесная доля электронов со спином
- равновесная доля электронов со спином![]() в конечном состоянии, тогда имеет место
соотношение
в конечном состоянии, тогда имеет место
соотношение
![]() ,
,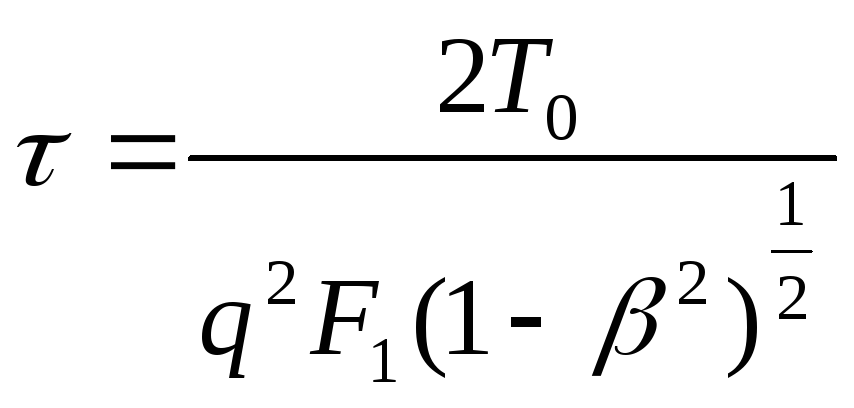 (3.31)
(3.31)
Отсюда
можно сделать глобальный вывод, что
если
![]() то преимущественной ориентации спина
нет (
то преимущественной ориентации спина
нет (![]() ),
если же, в свою очередь,
),
если же, в свою очередь,![]() ,
тогда возникнет преимущественная
ориентация, а время релаксации определяется
только величиной
,
тогда возникнет преимущественная
ориентация, а время релаксации определяется
только величиной![]() .
.
Положим,
что спиновый вектор
![]() и что он не зависит от углов
и что он не зависит от углов![]() ,
,![]() (т.е. от конечных квантовых чисел
электрона, зависящих от
(т.е. от конечных квантовых чисел
электрона, зависящих от![]() ,
,![]() ),
тогда интегрируя по
),
тогда интегрируя по![]() и учитывая (3.28) из (3.27) получим
и учитывая (3.28) из (3.27) получим![]() и эффект самполяризации отсутствует
[109]. Если же положить что
и эффект самполяризации отсутствует
[109]. Если же положить что![]() зависит от квантовых чисел электрона,
в конечном состоянии, то можно поставить
задачу найти такой
зависит от квантовых чисел электрона,
в конечном состоянии, то можно поставить
задачу найти такой![]() который обнаруживает максимальный
эффект самополяризации или, что тоже
самое, максимальное значение
который обнаруживает максимальный
эффект самополяризации или, что тоже
самое, максимальное значение![]() .
Зададимся этой задачей.
.
Зададимся этой задачей.
