Глава 3. Поляризационные эффекты при взаимодействии релятивистских частиц с плоской электромагнитной волной

10. Спонтанное излучение релятивистского электрона в поле плоской электромагнитной волны

Значительный интерес сохраняется к одному из фундаментальных процессов физики элементарных частиц - рассеянию фотонов на электроне.

Основополагающий результат работы [180], впервые полученный квазиклассическим методом, был строго обоснован в [181] и затем повторялся много раз другими авторами.

Здесь необходимо отметить, что наиболее полное рассмотрение излучения релятивистских частиц во внешних электромагнитных полях возможно только на основе квантовой теории, в соответствии с которой частицы и поле излучения представляют собой две квантовомеханические системы, которые взаимодействуют между собой даже при отсутствии в начальный момент времени фотонов. Этим взаимодействием и объясняются спонтанные переходы с испусканием фотонов.

Дифференциальное сечение эффекта Комптона в зависимости от поляризации всех участвующих в процессе частиц изучалось в [182, 183]. Дальнейшим развитием этой темы послужили появившиеся в 60-годы работы [184-189], в которых интенсивность налетающей на электрон электромагнитной волны принималась произвольно большой. Часть этих результатов, как оказалось, имелась в более ранней работе [190]. При расчетах в [184-189] использовались точные решения уравнения Дирака для электрона в поле плоской электромагнитной волны.

10.1 Волновые функции и квантовые числа электрона

Пусть плоская волна распространяется вдоль единичного вектора . В этой волне движется электрон. Электромагнитный 4-потенциал, соответствующий такой волне, имеет вид

, , (3.1)

где произвольная функция. Известно [20, 43], что в поле плоской волны интегралы движения можно записать как

,,(3.2)

где - энергия,- обобщенный импульс электрона,- постоянная Планка.

Пусть потенциал волны подчиняется условию

(3.3)

отсюда можно сделать вывод [20], что движение электрона в плоской волне является сложным и представляет собой некоторые колебания около некоторого фиксированного центра и дрейф этого центра со средней скоростью .

,,, (3.4)

,,

где - «эффективная масса» электрона

,,(3.5)

- масса покоя электрона

(3.6)

Безразмерный параметр γ², характеризующий интенсивность волны является релятивистским инвариантом.

Из (3.4) можно получить соотношения

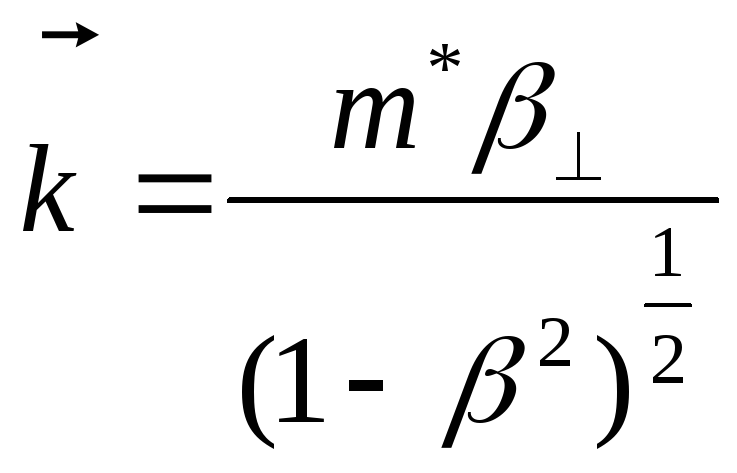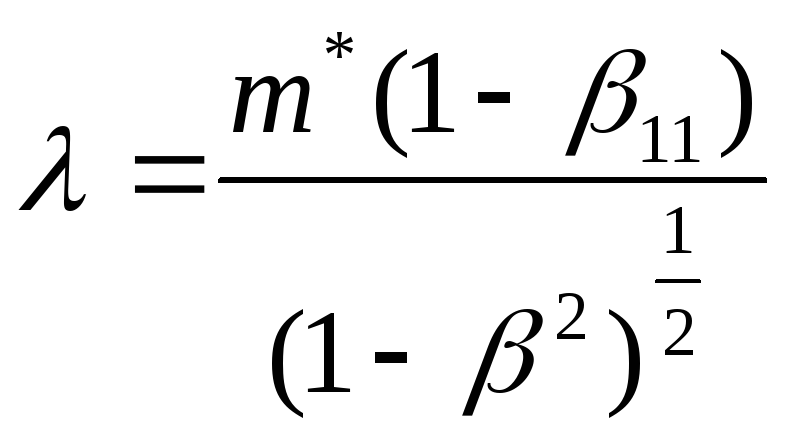,,(3.7)

Для скорости дрейфа будем использовать способ задания

,

,, (3.8)

,

В (З. 8) векторы ,- произвольные ортогональные единичные векторы, лежащие в плоскости, ортогональной вектору.

Тройка векторов ,,- является правой.

Величины и- в квантовой электродинамике также являются интегралами движения. В [42] получены волновые функции электрона, соответствующие состояниям с определенными значениямии.

Запишем эти волновые функции в блочной форме через двумерные матрицы Паули

(3.9)

,,

где - произвольный постоянный двухкомпонентный спинор, L нормировочная длина. Для уравнения Дирака, описывающее электрон в поле плоской волны, определен спиновый интеграл движения

,

,,

,

, (3.10)

Здесь ,- матрицы Дирака. Впервые такой интеграл найден в [109] (см. также [431]). При получении этого интеграла браликак постоянный вектор, не зависящий от,t.

Пусть волновая функция (3.9) подчиняется условию

,(3.11)

Тогда (3.11) удовлетворяется, если спинор описывается уравнением

,(3.12)

Установим смысл спинового оператора, также как и векторов и. Для этого перейдем в нерелятивистское приближение. В этом случае,и, следовательно, единичный векторопределяет направление ориентации спина. Назовем его спиновым вектором.

Однако в [109] и в [4З] опущена одна возможность. А именно: оператор (3.10) будет интегралом движения при условии, если - оператор (точнее - вектор-оператор) - интеграл движения. Тогда (3.11) и (3.12) по-прежнему выполняются но в (3.12) операторнеобходимо переменить на его собственное число.

Окончательно, состояние электрона в поле плоской волны будем характеризовать четырьмя квантовыми числами ,,(при заданном оператореR)