1.15. Влияние систематических ошибок на точность отдельных измерений

Закономерности возникновения случайных и систематических ошибок различны. Систематические ошибки подчиняются функциональным закономерностям, а случайные - статистическим. Рассмотрим влияние систематических ошибок на точность определения одного результата. Общая ошибка в этом случае составит

(1.73)

где _i - случайная составляющая общей ошибки измерения;

_i - систематическая составляющая.

В геодезической практике принято, если один из источников общей ошибки характеризуется средней квадратической ошибкой, не превышающей 1/3 средней квадратической ошибки, характеризующей другой источник, то первым можно пренебречь [ 3 ]

(1.74)

тогда

т.е. значение средней квадратической ошибки m, если пренебречь систематической ошибкой, уменьшится всего на 5%.

1.16. Оценка точности функции при наличии систематических ошибок

Определим совместное влияние случайных и систематических ошибок на отдельные результаты измерений. Будем считать, что общая ошибка содержит постоянную систематическую часть . Тогда ряд ошибок измерений предстанет в виде

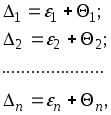(1.75)

где _i - общая ошибка измерений;

_i - случайная составляющая;

_i - систематическая составляющая.

Равенства (1.75) почленно возведем в квадрат

(1.76) Учитывая, что _  ₂    _n   , просуммируем полученные значения, а сумму разделим на n т.е.

(1.77)

Второй член правой части равенства (1.77) cогласно четвертому свойству случайных ошибок равен нулю. Переходя к средним квадратическим ошибкам, получим

(1.78)

Аналогично определяется средняя квадратическая ошибка функции

(1.79)

Первое слагаемое определяется согласно (1.47)

(1.80)

Величина систематической ошибки определится из следующего выражения [ 2 ]

(1.81)

Тогда (1.82)

1.17. Оценка точности равноточно измеренных величин при систематическом влиянии

Пусть слагаемые x₁, x₂, ... , x_n результаты равноточных измерений со средней квадратической ошибкой m_ и постоянной систематической ошибкой . Тогда при

y = x₁ + x₂ + ... + x_n

имеем (1.83)

где а

Тогда средняя квадратическая ошибка суммы составит

(1.84)

1.18. Принцип равных влияний

При проектировании геодезических работ рассчитывают точность предстоящих измерений, пользуясь формулами теории ошибок измерений. При этих расчетах встречается задача, в которой по известному виду функции F требуется рассчитать точность измерений аргументов. Чтобы иметь определенное решение, применяют принцип равных влияний.

Пусть дана функция общего вида

(1.86)

На основании равенства (1.47) средняя квадратическая ошибка функции общего вида определится

Предположим, что

Откуда

(1.87)

Эти соотношения позволяют вычислить средние квадратические ошибки аргументов при заданном M_y, т.е. определить необходимую точность измерений.