1 эт

1.1 Форма Земли и ее модели

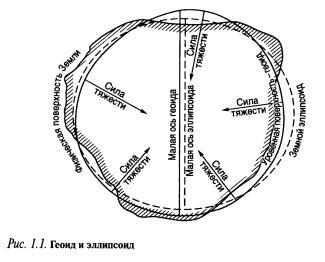
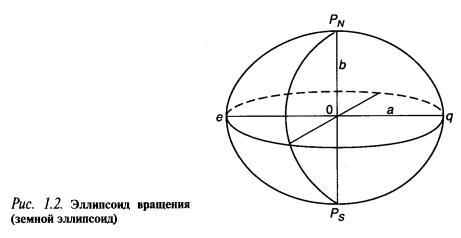
Штурманский метод решения задач судовождения требует знания закономерностей движения судна по поверхности Земли. Это возможно лишь при знании формы нашей планеты и ее основных размеров. Многовековые попытки решить эту научную проблему привели к представлению физической формы Земли в виде геоида — сглаженного тела, размеры которого наиболее близки к размерам нашей планеты. Геоид — тело, ограниченное невозмущенной поверхностью уровня Мирового океана, мысленно продолженной под материками и островами таким образом, что она в каждой своей точке перпендикулярна отвесной линии (рис. 1.1). Геоид получен экспериментально и его поверхность не может быть описана конечным математическим уравнением. Поэтому на поверхности геоида невозможно решать математические задачи судовождения. Возникает необходимость аппроксимации геоида другим телом — моделью Земли, имеющей простое математическое описание. При решении навигационных задач судовождения нашли применение две основные модели Земли: эллипсоид вращения (сфероид) и сфера (шар). Геоид очень близок по форме к эллипсоиду вращения, образованному вращением эллипса вокруг малой оси. Эллипсоид вращения — математически правильная фигура. Именно поэтому для решения задач геодезии, судовождения и картографии с высокой точностью за модель Земли принимают эллипсоид вращения и называют его земным эллипсоидом (рис. 1.2).

Размеры и форму эллипсоида определяют его элементы: большая полуось а, малая полуось b, сжатие, эксцентриситет  Для наилучшего представления о геоиде в целом используют земной эллипсоид и определяют его так, чтобы:

• объем эллипсоида был равен объему геоида;

• плоскость экватора и малая ось эллипсоида совпадали соответственно с плоскостью экватора и осью вращения Земли;

• сумма квадратов отклонений геоида от общего земного эллипсоида по всей их поверхности была наименьшей.

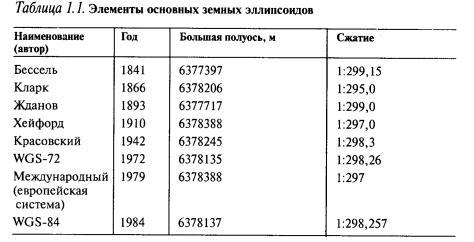
В 1964 г. на XII конгрессе Международного астрономического союза был принят общий земной эллипсоид, который хорошо согласуется со всей поверхностью геоида. Его размеры: а = 6378160 м; а = 1: 298,5. В наши дни для решения геодезических и навигационных задач широко используются общие земные эллипсоиды (World Geodetic System), разработанные в разные годы: WGS-72, WGS-84, элементы которых даны в табл. 1.1. Для наилучшего же представления формы геоида в определенной области земной поверхности (территории отдельной страны) подбирают наиболее подходящий земной эллипсоид и определяют его так, чтобы:

• плоскость экватора и малая ось эллипсоида были параллельны соответственно плоскости экватора и оси вращения Земли; • сумма квадратов отклонений геоида от этого эллипсоида в пределах заданной области была наименьшей.ъ

Земной эллипсоид с определенными размерами, соответствующим образом ориентированный в теле Земли и принятый за модель Земли в государстве, называется референц-эллипсоидом. Положение референц-эллипсоида в теле Земли определяется исходными геодезическими датами:

• координатами точки, в которой выполнена взаимная привязка геоида и эллипсоида; • направлением между двумя объектами на поверхности Земли; • высотой геоида над референц-эллипсоидом.

В нашей стране с 1946 г. в качестве модели Земли принят эллипсоид, элементы которого были определены под руководством профессора Ф. Н. Красовского. При этом использовались результаты измерений, выполненных на территории СССР, стран Западной Европы и США. Этот эллипсоид получил название референц-эллиписоида Красовского. Его элементы: большая полуось а = 6378245 м,

малая полуось b = 6 356 863 м, сжатие α = 1:298,3, эксцентриситет е = 0,0818. Положение (ориентировка) эллипсоида Красовского определяется:

• координатами центра круглого зала Пулковской обсерватории (широта 59°46'18,55", долгота 30° 1942,09"); • направлением из этой точки на пункт Бугры  (азимут 121° 10'38,79"); • нулевой разностью высот геоида и референц-эллипсоида Красовского в Пулкове. В различных государствах рассчитаны и используются в качестве моделей Земли референц-эллипсоиды различных размеров (табл. 1.1). При решении многих задач навигации, не требующих повышенной точности, Землю принимают за шар определенного радиуса R. При этом для определения размеров земного шара могут быть поставлены различные условия, например:

• объем земного шара равен объему земного эллипсоида  при этом Подставив значения полуосей эллипсоида Кра- совского, получим значение радиуса земного шара R = = 6371109,7 м;  • поверхность шара равна поверхности эллипсоида, при этом Для эллипсоида Красовского R = 6371116 м;  • радиус земного шара равен среднему радиусу кривизны ограниченного участка территории эллипсоида, расположенного в широте φ, при этом  • длина одной минуты дуги большого круга шара равна одной морской миле; при этом R — 6366707 м.