Алгоритм минимизации функций в классе кнф

Чтобы построить все минимальные КНФ (МКНФ) функцииf, следует построить все МДНФ функцииfи взять от каждой из них отрицание, для чего заменить знаки & на, ана & ( сохранив первоначальное распределение скобок) и над каждой буквой поставить знак отрицания. Полученные КНФ для функцииfбудут минимальными. В самом деле, если бы дляfсуществовала КНФ с меньшим числом букв, то ее отрицание дало бы дляf ДНФ с меньшим числом букв, чем в любой из минимальных ДНФ дляf. Противоречие с их минимальностью.

Алгоритм минимизации функций в классе нормальных форм

Пусть f– функция алгебры логики.

1. Строим все МДНФ функции f.

2. Строим все МКНФ функции f.

3. Из построенных минимальных форм выбираем простейшие ( по числу букв).

Пример 6. В классе нормальных форм минимизировать функциюf=(01011110).

1. Строим СДНФ для функции f:

2. Строим сокращенную ДНФ функции f:

3. Строим матрицу покрытий (таблица 3.6).

Таблица 3.6

N	ПИ	xy z x y z xyz xy z x yz
1 2 3 4	x z y z xy xz	+ + + + + + + +

Решеточное выражение E= ( 12 ) 1 (34 ) 4 = 134124.

4. Строим все тупиковые ДНФ функции f:

5. Обе построенные ТДНФ являются минимальными.

6. Повторяем эти этапы для функции f.

СДНФ :

Сокращенная ДНФ :

Строим матрицу покрытий (таблица 3.7).

Таблица 3.7

N	ПИ	xyz x yz x y z
1 2	xz x y z	+ + +

Решеточный многочлен E= 112 = 12. Единственная тупиковая ДНФ (она же минимальная) для функции Минимальная КНФ функции Из построенных МДНФ и МКНФ выбираем простейшую

Пример 7.В классе нормальных форм минимизировать функциюf=(11011011).

1. СДНФ:

2. Сокращенная ДНФ : =

3. Строим матрицу покрытий (таблица 3.8).

Таблица 3.8

N	ПИ	xyz xy z x y z xyz x yz x y z
1 2 3 4 5 6	x y xz yz x z y z xy	+ + + + + + + + + + + +

E= ( 36 ) ( 46 ) ( 45 ) ( 23 ) ( 12 ) ( 15 ) = 124613561342562345.

4. Тупиковые ДНФ функции f:

5. Минимальные ДНФ функции f:

6. Повторяем указанные выше этапы для функции f.

СДНФ :

Сокращенная ДНФ :

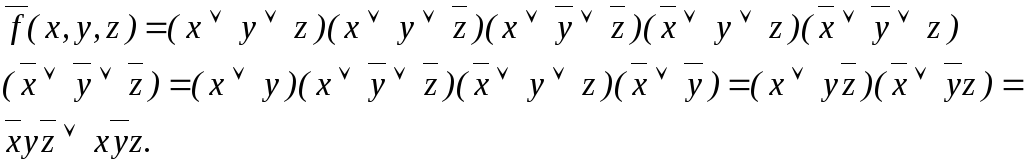
Построенная сокращенная ДНФ функции fявляется для нее тупиковой и минимальной .

Минимальная КНФ функции

Построенные МДНФ и МКНФ имеют одно и то же число букв; все они составляют минимальные формы для f: