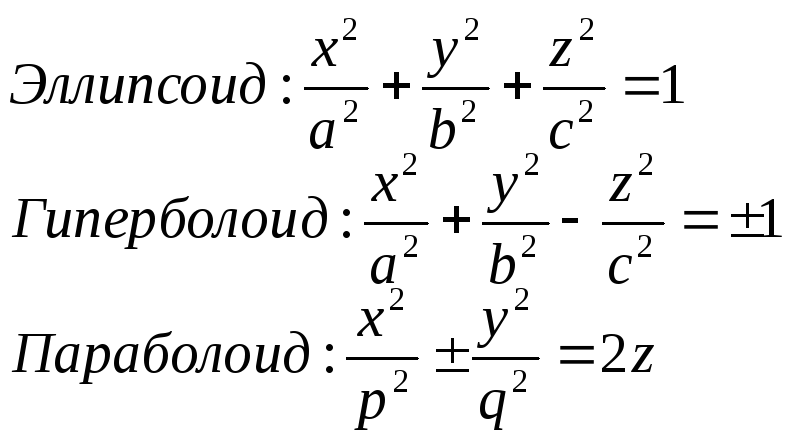anal

Шпаргалка по аналитичнской геометрии.

Полярные координаты: x= cos, y= sin, .

Деление отрезка в данном соотношении:

Площадь треугольника:

Преобразование координат при неизменном масштабе: x=x’ cos  - y’ sin  + a

y= y’ cos  - x’ sin  + b

Прямая.

tg =(k₂–k₁)/(1–k₁k₂), Ур-е прямой в отрезках: , нормальное уравнение прямой: xcos+ysin–p=0, =x*cos+y*sin–p, d=||, , полярное уравнение прямой: =p/cos(–), перпендикулярно {p, }.

Эллипс:

, r_1,2=ax, директриса обладает следующим свойством: если r – расстояние произвольной точки эллпса до некторого фокуса, d – расстояние от этой же точки до односторонней с этим фокусом директрисой, то (r/d)=. Если в ур-нии эллипса a>b, то у-ние директрис: x=(a/) и y=(b/) если b>a.

Гипербола:

=(c/a), директрисы: x=(a/). Каждая директриса обладает след. свойством: если r – расстояние от произвольной точки гиперболы до некоторого фокуса, d – расстояние от этой точки до одностороннего с этой точкой фокуса, то (r/d)=.

Парабола:

y=2px, директриса: x=–p/2. r=x+(p/2).

Диаметр.

Диаметр эллипса, сопряжённый хордам с угл. коэф. k определяется уравнением: y=–(b²/a²k)x.

То же для гиперболы: y=(b²/a²k)x.

Все диаметры параболы параллельны её оси, если y²=2px, y=p/k.

Упрощение общего уравнения линий второго порядка.

Ax²+2Bxy+Cy²+2Dx+2Ey+F=0.

Центром некоторой линии наз. такая точка плоскости, по отношению к которой точки этой линии расположены симметрично парами. Линии второго порядка, обладающие единственным центром, наз. центральными. Точка S(x₀; y₀) есть центр линии если:

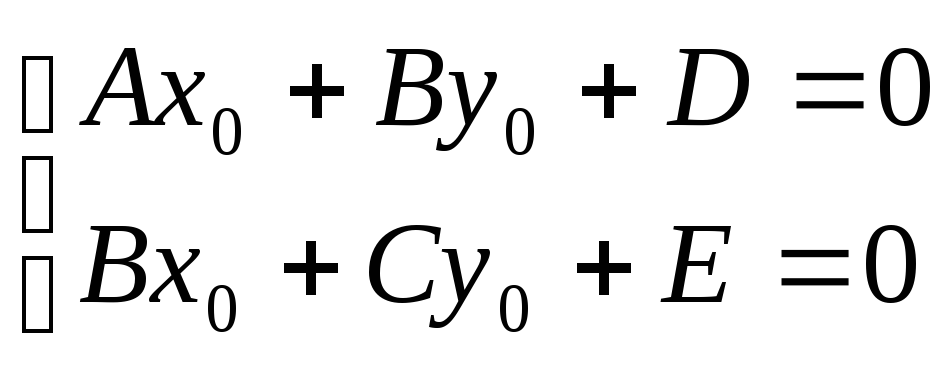
Пусть 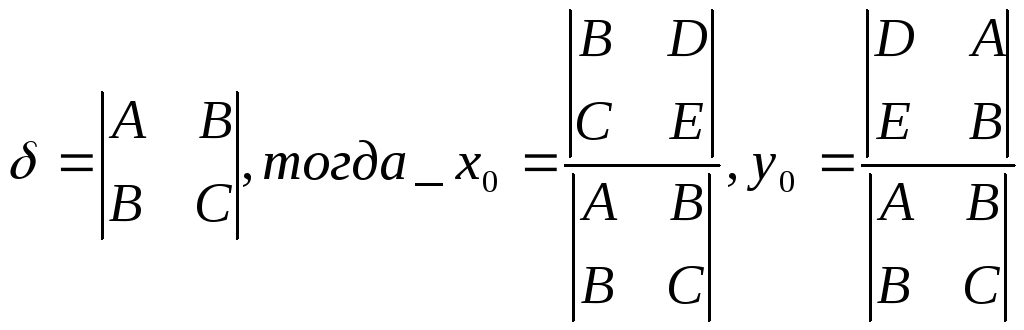, неравенство 0 служит признаком центральной линии 2-го порядка.

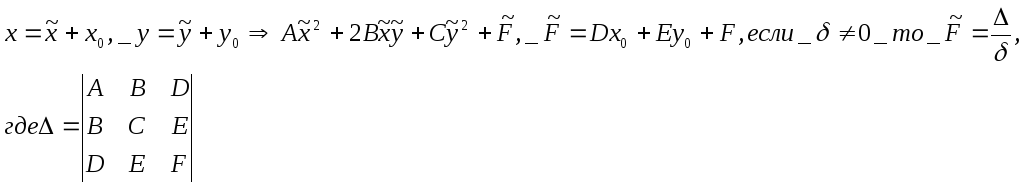Дальнейшее упр. ур. достигается при помощи преоб. координат: и если  выбран так, что: Btg²–(C–A)tg–B=0  A’x’² + C’y’² + .

Преобразование параболы.

Е сли =0, то линия либо не имеет центра, либо имеет бесконечно много центров. Сначала повернём:

Btg²–(C–A)tg–B=0, тогда в новых координатах ур-е линии приводится к :

A’x’²+2D’x’+2E’y’+F=0, если А’0 и к C’y’²+2D’x’+2E’y’+F=0, если C’0.

Если параболическое уравнение представлено в виде (x+y)²+2Dx+2Ey+F=0, то дискриминатн левой части данного уравнения =–(D–E)², затем при помощи стандартного поворота на tg=–/ параболичское уравнение приводится к виду: C’y’²+2D’x’+2E’y’+F=0, где С’=²+², D’=, а параметр параболы: .

Дальнейшее упрощение ур-ий достигается путём параллельного переноса (повёрнутых) осей.

Векторное произведение векторов.

[ ab]=–[ba]=Se=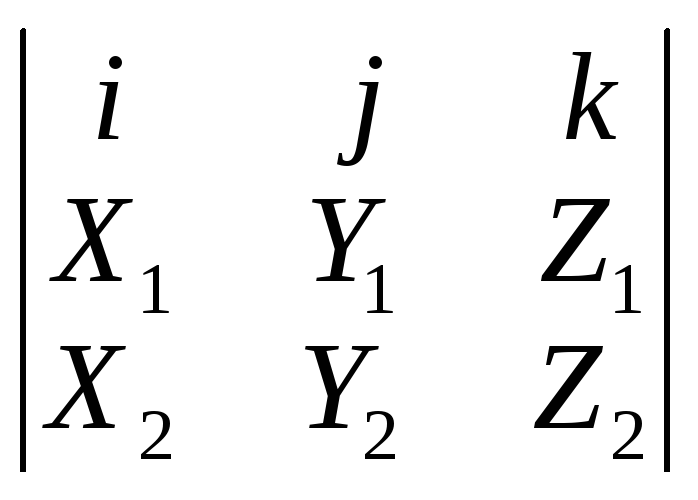, |[ab]|=S=|a| |b|sin .. .abc=[ab]c=a[bc]

Если abc=0, то a, b и c компланарны и наоборот.

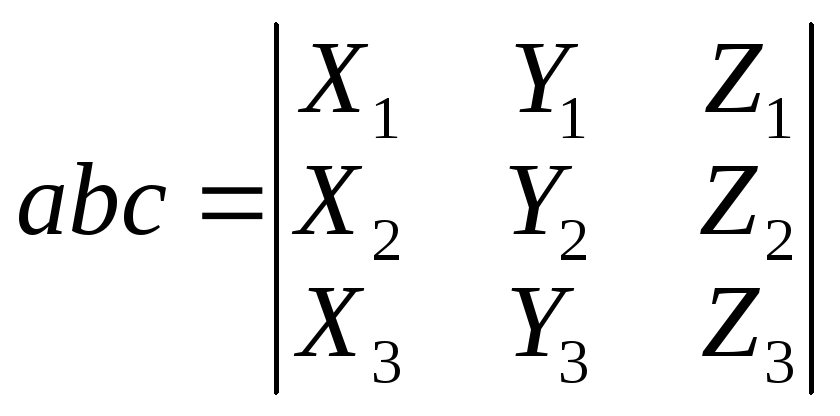
Двойное векторное произведение: [[ab]c][a[bc]], [[ab]c]=b(ac)–a(bc).

[ab][bc][ca]=(abc)² [a[b[c[d]]]=[ac](bd)–[ad](bc)=(acd)b–(ab)[cd]

[ab]²[ac]²–([ab][ac])²=a² (abc)² [[ab][bc]] [[bc][ca]] [[ca][ab]]=a(bcd)

.

Плоскость и прямая в пространстве.

Знак нормирующего множителя берётся противоположным знаку свободного члена нормируемого уравнения. Отклонение положительно если точка и начало координат лежат по разные стороны.

Поверхности второго порядка.

3