teormeh / CH_09

Глава 9

ЛИНЕЙНЫЕ КОЛЕБАНИЯ СИСТЕМ

9.1. СИСТЕМЫ С ГИРОСКОПИЧЕСКИМИ СИЛАМИ

Введение обобщенного потенциала , где , позволяет описывать гироскопические силы. Мощность гироскопических сил равна нулю, и в случае они не вносят вклад в интеграл обобщенной энергии

,

поэтому гироскопические силы не меняют положения равновесия системы. Однако гироскопические силы могут существенно изменить характер движения.

Рассмотрим движение заряженной частицы массы заряда в магнитном поле. Пусть на частицу действует поле, направленное вдоль оси OZ инерциальной системы отсчета, и кроме того, на нее действуют потенциальные силы, энергия которых определяется формулой (пространственный осциллятор).

Выберем вектор-потенциал магнитного поля

.

Вектор-потенциал определен неоднозначно, поскольку функция Лагранжа определена с точностью до преобразования

не меняющего уравнений движения. В рассматриваемом случае функция Лагранжа

(1.9)

приводит к уравнениям движения - линейным однородным уравнениям с постоянными коэффициентами:

(2.9)

Здесь введены обозначения . Движение вдоль оси OZ определяется лишь полем осциллятора и происходит по гармоническому закону:

.

Движение в плоскости OXY не зависит от движения вдоль оси OZ и определяется обычным образом с помощью подстановки Эйлера

,

что дает систему уравнений для определения комплексных коэффициентов :

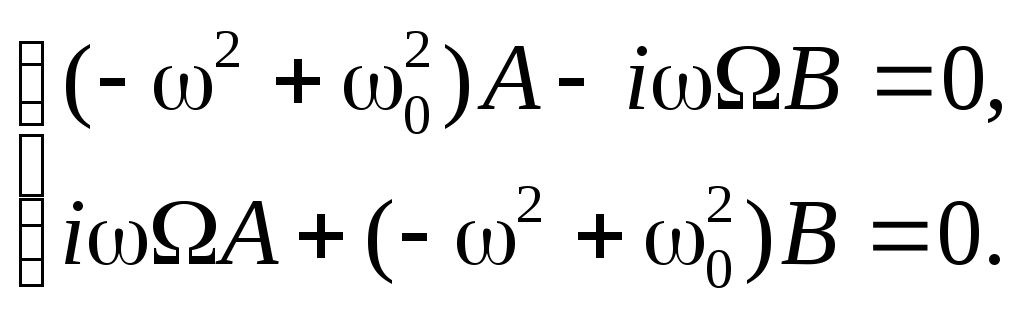
Нетривиальное решение системы существует при значениях , определяемых из характеристического уравнения

, (3.9)

где - ларморовская частота.

Соответствующая этим частотам связь между комплексными коэффициентами :

(4.9)

приводит (после выделения действительной части) к решению системы в виде

Таким образом движение частицы в магнитном поле может быть представлено как суперпозиция вращений по окружностям радиусов и с соответствующими частотами и :

.

В предельном случае слабого поля

т. е. движение можно рассматривать как вращение пространственного с частотой .

Этот результат является частным случаем теоремы Лармора о движении заряженных частиц в слабом магнитном поле:

Движение (взаимодействующих) заряженных частиц с одинаковым отношением заряда к массе в однородном магнитном поле в инерциальной системе отсчета эквивалентно движению этих же частиц во вращающейся системе отсчета в отсутствие магнитного поля, если угловая скорость вращения вокруг неподвижной оси, проходящей через начало координат, достаточно мала, так что для всех частиц выполняется соотношение .

Рассмотрим систему частиц, взаимодействие которых друг с другом и с внешними полями описывается потенциальной энергией . Функция Лагранжа такой системы имеет вид:

.

Движение этой же системы в однородном магнитном поле может быть описано функцией Лагранжа :

,

а движение в системе, вращающейся с угловой скоростью вокруг неподвижной оси, проходящей через начало координат (в отсутствие магнитного поля), - функцией :

.

Здесь учтена связь между скоростями частиц в лабораторной и движущейся системе: .

Функциональная зависимость и . одинакова, если угловая скорость вращения системы равна ларморовской частоте , а последнее слагаемое в , пропорционально квадрату угловой скорости, пренебрежимо мало. Это и доказывает теорему.

Отсюда следует, что движение частиц с одинаковым отношением заряда к массе в слабом магнитном поле можно рассматривать как прецессию с частотой Лармора.

Полная энергия осциллятора в магнитном поле представляется как сумма энергий в каждой моде: , где . Это решение справедливо при любой величине магнитного поля. В сильном магнитном поле при , а . В этом пределе , а .

Достаточно сильное магнитное поле способно сделать финитным даже движение в окрестности точки неустойчивого равновесия. Этот случай можно рассмотреть, проведя в уравнениях движения замену . В этом случае потенциальная энергия точки имеет максимум в начале координат, и в отсутствие магнитного поля частица экспоненциально быстро уходит из начала координат. Включение магнитного поля приводит к изменению характера движения. Решение характеристического уравнения в этом случае дает спектр вида . Колебательное решение существует при , то есть при . Соотношение между комплексными амплитудами для собственных частот приводит к закону движения

Этим модам соответствуют энергии колебаний

и .

Последнее выражение интересно тем, что уменьшение полной энергии частицы сопровождается ростом амплитуды колебаний (радиуса окружности ), что свидетельствует о неустойчивости этой моды.

Этот результат является общим для всех систем с гироскопическими силами. Пусть взаимодействие материальных точек допускает описание с помощью обобщенно-потенциальных сил

.

Предположим также, что , т. е. связи в системе могут явно зависеть от времени или движение может описываться в неинерциальной системе отсчета. В этом случае кинетическая энергия имеет вид

,

и функция Лагранжа может содержать линейные по обобщенным скоростям члены.

Условие равновесия соответствует изолированному минимуму обобщенной энергии

и определяется условием

.

Выберем обобщенные координаты так, чтобы точка была точкой равновесия (здесь мы рассматриваем относительное равновесие в обобщенных координатах ). Предположим, что, как и в случае потенциальных сил , т. е. является интегралом, а положительно определенная квадратичная форма обобщенных скоростей:

В отношении разности , входящей в обобщенную энергию, мы не будем делать такого предположения:

.

Уравнения движения в данном случае имеют вид

. (5.9)

Здесь

антисимметричная матрица, соответствующая выбранному положению равновесия, в которой определяются уравнением:

.

Будем искать решение системы (5.9) в виде

где - комплексная амплитуда. Подстановка в уравнения движения приводит к системе уравнений для определения собственных частот (из условия существования нетривиальных решений

,

и коэффициентов - амплитуд:

. (6.9)

Как и в случае потенциальных сил, общие свойства решений можно исследовать, умножая (6.9) на сопряженную амплитуду и проводя суммирование по повторяющемуся индексу. Учитывая свойства билинейных форм, возникающих в уравнении

,

а именно для нетривиальных решений коэффициент

в силу положительной определенности и симметрии матрицы . Действительная величина

в случае локального минимума обобщенной энергии положительна, а антисимметричная матрица порождает билинейную форму

в которой тоже оказывается действительной.

Таким образом, для любого нетривиального решения собственные частоты системы удовлетворяют уравнению

,

имеющему решения

Отсюда следует, что для любых при решение носит колебательный характер. Более того, даже в случае когда в системе имеется локальный максимум обобщенной энергии, при выполнении соотношения , т. е. при достаточно больших гироскопических силах, движение остается колебательным. В этом проявляется стабилизирующее влияние гироскопические сил на систему.

Собственные векторы , соответствующие собственным частотам , являются ортогональными, как и в случае потенциальных сил. Действительно, умножая (6.9) с на , а соответствующее решение при на , получим систему уравнений

Напомним, что здесь всюду проведено суммирование по повторяющимся индексам. Вычитая первое уравнение из второго, получим

Здесь мы ввели обозначение

.

Из симметрии матрицы , следует, что , а антисимметричность матрицы приводит к условию

,

откуда при , а следовательно, и при .

Ортогональность решений позволяет записать обобщенную энергию в виде суммы

,

где

.

Частоты удовлетворяют условию

,

поэтому для действительных собственных частот системы

энергия

при любых значениях с, и положительных и отрицательных, если величина напряженности магнитного поля достаточна для стабилизации. Для собственных частот

знак энергии

определяется знаком коэффициента с: если движение происходит вблизи локального максимума потенциальной энергии , то , а в случае движения в окрестности неустойчивого равновесия энергия, соответствующая таким модам колебаний, будет отрицательной (при выполнении условия стабилизации ).

Полученные могут быть полезны и в задачах об исследовании устойчивости движения, если они могут быть сведены к анализу устойчивости относительного равновесия во вращающихся системах отсчета. Такой подход мы рассмотрим на примере движения частиц в окрестности треугольных точек Лагранжа.

Рассмотрим круговую ограниченную задачу трех тел. Пусть две точечные массы и обращаются вокруг общего центра масс по круговым орбитам. Пробное тело массы движется в гравитационном поле масс и , не влияя на их движение. Пусть расстояние между точками и равно (рис. 2.9).

В инерциальной системе отсчёта движение точек вокруг общего центра масс происходит с углевой скоростью, определяемой из условия

Координаты точек во вращающейся системе удовлетворяют условию

.

Учитывая, что частоты обращения получим

, где .

При этом

Начало координат вращающейся системы совпадает с центром масс. Координаты точки во вращающейся системе связаны с координатами инерциальной системы соотношениями

где

Кинетическая энергия точки имеет вид

(7.9)

а ее потенциальная энергия -

(8.9)

Функция Лагранжа содержит линейные по скоростями члены, которые во вращающейся системе OXY приводят к появлению гироскопических сил, поскольку слагаемые и в этой системе естественно интерпретируются как проявление сил инерции.

Положение равновесия относительно координат OXY определяется условием

что дает для положения равновесия

Таким образом, в системе имеются точки, образующие равносторонний треугольник, такие, что пробное тело находится в них в положении относительного равновесия. Эти точки называются треугольными точками Лагранжа

Рассмотрим малые отклонения от положения равновесия. Пусть - малые отклонения от положения равновесия. Функция Лагранжа, приводящая к линейным уравнениям движения в переменных , имеет вид

,

где введено обозначение .

Потенциальная энергия в точке имеет максимум, так что относительное положение равновесия является неустойчивым.

Уравнения движения точки в плоскости OXY в линейном приближении имеют вид

(10.9)

Действие гироскопических сил, как отмечалось ранее, может стабилизировать движение. Для исследования этой возможности будем искать решения этих уравнений в виде

Подставим эти выражения в (10.9) и получим систему уравнений для определенных коэффициентов:

Условие существования нетривиального решения дает собственные значения :

.

Колебательный режим возможен в случае, когда соотношение масс удовлетворяет условию

.

В частности, в системе Земля - Луна, если пренебречь влиянием Солнца, возможны колебания частиц вблизи треугольных точек Лагранжа. Подставляя значение отношения масс для этого случая , получим возможные частоты колебаний

.

Таким образом, движение относительно вращающейся системы координат вблизи рассматриваемой треугольной точки Лагранжа стабилизируется гироскопическими силами.

9.2. ВЛИЯНИЕ ДИССИПАТИВНЫХ СИЛ

Рассмотрим, наконец, влияние диссипативных тел на движение системы. В отличие от обобщенно - потенциальных сил их нельзя описать с помощью натуральной функции Лагранжа , поэтому необходимо построить обобщенные диссипативные силы

Диссипативные силы, такие как трение, направлены в сторону противоположную относительному движению тел, и могут как увеличивать, так и уменьшать энергию системы.

Рассмотрим простейший случай сил сопротивления, пропорциональных скорости движения точек:

, .

В этом случае мощность диссипативных сил отрицательна:

,

что приводит к уменьшению энергии системы точек.

При использовании метода Лагранжа, однако, существует теорема об изменении обобщенной энергии, а не полной, поэтому в системе со связями, явно зависящими от времени, или при использовании обобщенных координат , где явно включена зависимость от времени , диссипативные силы не приводят обязательно к уменьшению обобщенной энергии:

Для описания диссипативных сил рассматриваемого типа удобно использовать диссипативную функцию Рэлея где - симметричная матрица. Ограничимся далее анализом лишь тех сил, для которых диссипативная функция Рэлея отрицательна, а матрица - положительно определенная. В нашем случае это соответствует силам, пропорциональным скорости при условии, что преобразование к обобщенным координатам явно не содержит времени.

В приближении линейных уравнений движения положим , предполагая, что движение происходит лишь в окрестности начала координат. В этом случае обобщенные диссипативные силы

Рассмотрим вначале простейший пример - движение линейной системы с двумя степенями свободы с учетом сопротивления среды. Пусть система состоит из двух одинаковых материальных точек, соединенных пружинами, жесткость каждой из которых . Точки могут двигаться вдоль оси инерциальной системы. Предположим, что коэффициенты и характеризуют сопротивление среды, причем Уравнения движения с учетом диссипативных сил имеют вид