
InformatikaMetodicheskieUkazania (1)
.pdf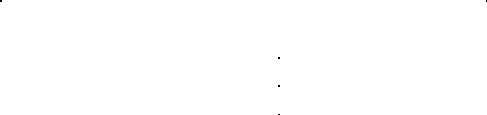
Импликация (условное высказывание) в русском языке выражается союзами «Если…то»; «Когда…тогда»; «Коль скоро…то» и т.п. Импликация обозначается знаком →. Это двухместная операция, записывается в виде А → В.
Эквивалентность в русском языке выражается союзами «Если и только если»; «Тогда и только тогда, когда». Эквивалентность обозначается знаком ↔.
Приведем таблицы истинности для рассмотренных логических операций.
A |
B |
A B |
A B |
A |
A B |
A B |
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
|
|
|
|
|
|
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
В таблице значение ИСТИНА обозначено через 1, а значение ЛОЖЬ – 0. Порядок всех пяти логических операций по убыванию старшинства сле-
дующий: отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность. Логическая формула (логическое выражение) – формула, содержащая лишь
логические величины и знаки логических операций. Результатом вычисления логической формулы является ИСТИНА или ЛОЖЬ.
Пример 3.2. Определите истинность формулы
F = ((C B) → B) (A B) → B.
Для решения задачи построим таблицу истинности этой формулы, перебрав все варианты значений логических переменных. Определим правила построения этих таблиц.
1.В заголовок таблицы выносятся все переменные в порядке их следования
вформуле.
2.Если n –количество переменных, то строк в таблице будет 2 × n.
3.Первая колонка заполняется наполовину значением 1 (истина), наполовину 0 (ложь).
4.Последующие столбцы заполняются по правилу: первая половина значений 1 предыдущего столбца заполняется 1, вторая 0, так же и для 0.
5.В последнем столбце значения 1 и 0 чередуются.
C |
B |
A |
C B |
(C B) → B |
A B |
((C B) → B) (A B) |
F |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
Ответ: Формула является тождественно истинной.
33
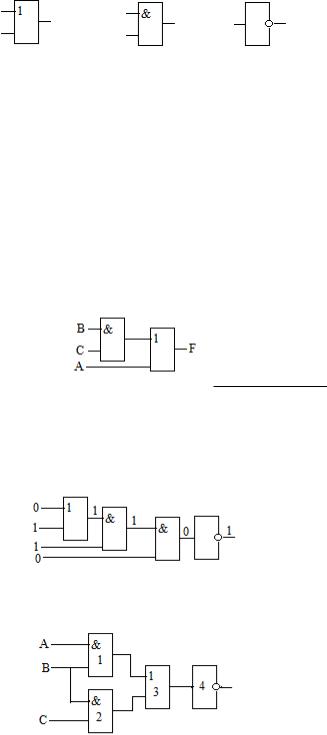
3.3. Логические схемы
Удобным способом представления логических выражений являются логические схемы. Вот как изображаются на таких схемах три основные логические операции:
Дизъюнкция Конъюнкция Отрицание Эти схемы называются вентилями.
Алгоритм построения логических схем следующий.
1.Определите число логических переменных.
2.Определите количество базовых логических операций и их порядок.
3.Изобразите для каждой логической операции соответствующий ей вен-
тиль.
4.Соедините вентили в порядке выполнения логических операций.
Пример 3.3. Нарисовать логическую схему выражения А В С. Количество логических переменных равно 3. Количество базовых логиче-
ских операций равно 2. Порядок выполнения операций в соответствии с приоритетом: сначала выполняется конъюнкция , а затем дизъюнкция .
Пример 3.4. Вычислить значение выражения ( А (В С) D) с помощью логической схемы. А = 0; В = 1; С = 1; D = 0.
Количество логических переменных равно 4. Количество базовых логических операций равно 4. Порядок выполнения операций: операция дизъюнкции В ˅ С , затем первая и вторая конъюнкции, последняя операция – отрицание.
Ответ: Значение выражения равно 1.
Пример3.5. Дана логическая схема. Построить соответствующее ей логическое выражение.
Строим таблицу входов и выходов каждого вентиля в соответствии с нумерацией.
34
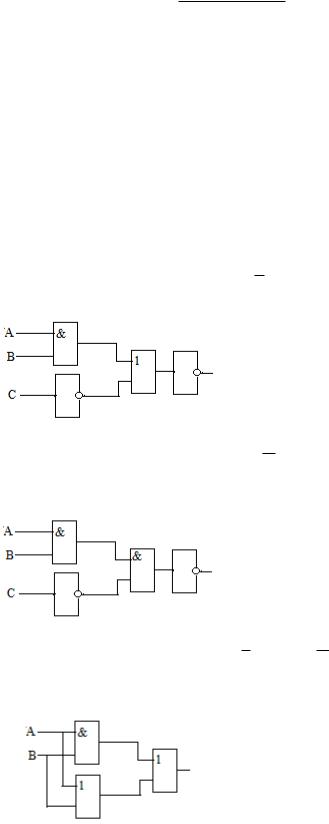
Вентиль |
Вход |
|
Выход |
|
1 |
А, В |
А В |
||
2 |
В, С |
В С |
||
3 |
А В; В С |
(А В) (В С) |
||
4 |
(А В) (В С) |
|
|
|
|
А В) (В С) |
|||
|
|
|
|
|
Ответ: логическая схема реализует функцию А В) (В С) .
3.4. Задания для самостоятельного выполнения
Указания к выполнению задания
1.Прочитайте теоретический раздел и разберите примеры 3.1–3.5.
2.Отчет должен содержать условие задачи. Таблицы и схемы должны быть построены аккуратно с использованием линейки и карандаша. Неаккуратно оформленные задания приниматься не будут. Решение каждой задачи должно содержать необходимые пояснения.
Вариант 1
1.Построить таблицу истинности для формулы Х ((X Y ) (X Y ) .
2.Построить логическую схему по формуле A B C A.
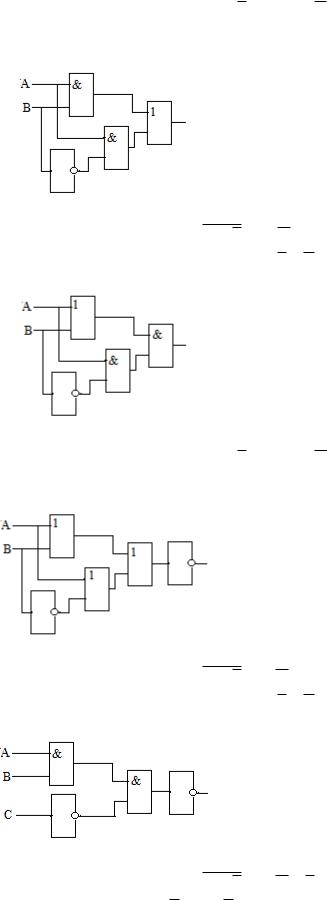
3.Определить логическую функцию, реализуемую логической схемой
Вариант 2
1.Построить таблицу истинности для формулы ( X Y X ) (Y X ) .
2.Построить логическую схему по формуле (A B) (C D) .
3.Определить логическую функцию, реализуемую логической схемой
Вариант 3
1.Построить таблицу истинности для формулы ((X Y ) Y ) (X Y ) .
2.Построить логическую схему по формуле (A B) (C B) .
3.Определить логическую функцию, реализуемую логической схемой
35
Вариант 4
1.Построить таблицу истинности для формулы ((X Y ) Y ) (X Y ) .
2.Построить логическую схему по формуле (A B) (C D) .
3.Определить логическую функцию, реализуемую логической схемой
Вариант 5
1.Построить таблицу истинности для формулы ( X Y ) (X Y ) .
2.Построить логическую схему по формуле A B C A B C .
3.Определить логическую функцию, реализуемую логической схемой
Вариант 6
1.Построить таблицу истинности для формулы ((X Y ) Y ) ( X Y ) .
2.Построить логическую схему по формуле A B C A.
3.Определить логическую функцию, реализуемую логической схемой
Вариант 7
1.Построить таблицу истинности для формулы ( X Y ) (X Y ) .
2.Построить логическую схему по формуле A B C A B C .
3.Определить логическую функцию, реализуемую логической схемой
Вариант 8
1.Построить таблицу истинности для формулы ( X Y ) (X Y ) .
2.Построить логическую схему по формуле B C A B .
36
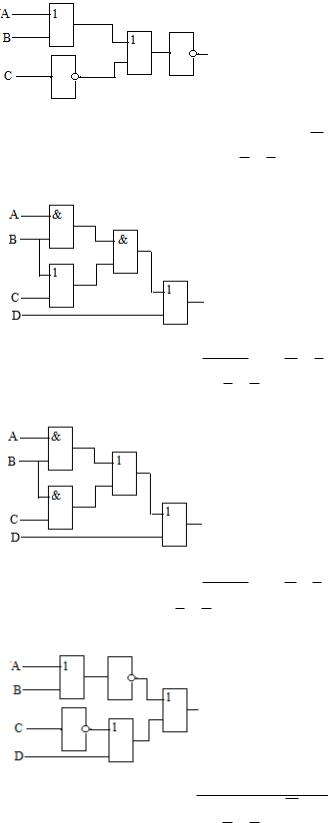
3. Определить логическую функцию, реализуемую логической схемой
Вариант 9
1.Построить таблицу истинности для формулы (X Y Y ) (X Y ) .
2.Построить логическую схему по формуле ( A B) ( A B) .
3.Определить логическую функцию, реализуемую логической схемой
Вариант 10
1.Построить таблицу истинности для формулы ( X Y ) ( X Y ) .
2.Построить логическую схему по формуле A B A B.
3.Определить логическую функцию, реализуемую логической схемой
Вариант 11
1.Построить таблицу истинности для формулы ( X Y ) ( X Y ) .
2.Построить логическую схему по формуле ( A B) ( A B) .
3.Определить логическую функцию, реализуемую логической схемой
Вариант 12
1.Построить таблицу истинности для формулы ( X Y ) ( X Y ) .
2.Построить логическую схему по формуле A B B C .
3.Определить логическую функцию, реализуемую логической схемой
37
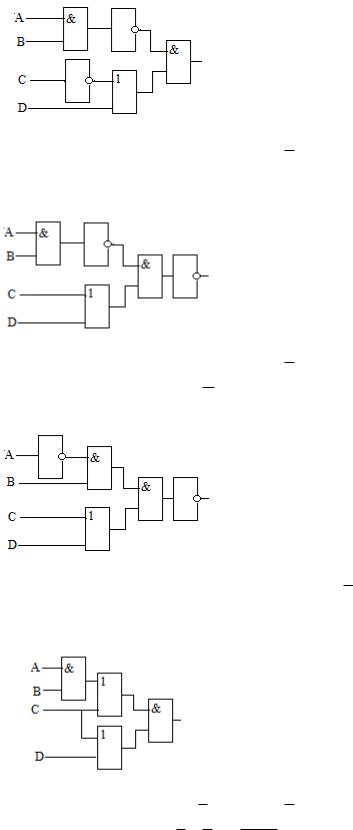
Вариант 13
1.Построить таблицу истинности для формулы А В (С А С) .
2.Построить логическую схему по формуле (A C) (B C) .
3.Определить логическую функцию, реализуемую логической схемой
Вариант 14
1.Построить таблицу истинности для формулы А В (С А С) В .
2.Построить логическую схему по формуле ( A D) (B D) .
3.Определить логическую функцию, реализуемую логической схемой
Вариант 15
1.Построить таблицу истинности для формулы А В (С А С) В .
2.Построить логическую схему по формуле A B C D .
3.Определить логическую функцию, реализуемую логической схемой
Вариант 16
1.Построить таблицу истинности для формулы А В (С А С) В .
2.Построить логическую схему по формуле ( A B) ( A B) .
3.Определить логическую функцию, реализуемую логической схемой
38
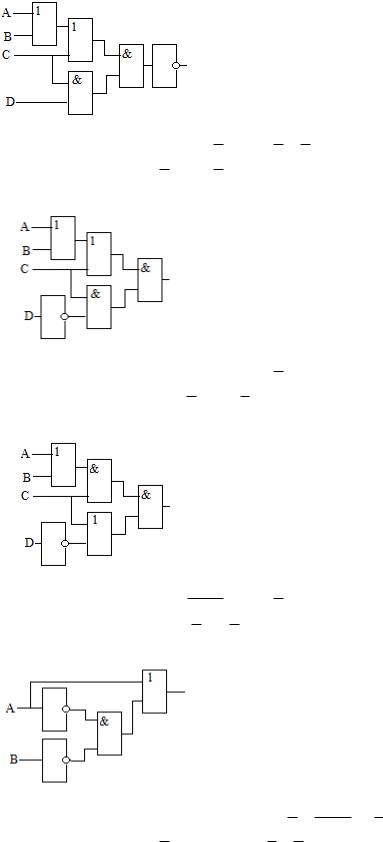
Вариант 17
1.Построить таблицу истинности для формулы А В (С А С) В .
2.Построить логическую схему по формуле A B C D .
3.Определить логическую функцию, реализуемую логической схемой
Вариант 18
1.Построить таблицу истинности для формулы А В (С А А С) В .
2.Построить логическую схему по формуле A B C A.
3.Определить логическую функцию, реализуемую логической схемой
Вариант 19
1.Построить таблицу истинности для формулы А В (С А А С) .
2.Построить логическую схему по формуле (A B) (C D) .
3.Определить логическую функцию, реализуемую логической схемой
Вариант 20
1.Построить таблицу истинности и для формулы А В (С А А С) В .
2.Построить логическую схему по формуле A B C A B C .
3.Определить логическую функцию, реализуемую логической схемой
39
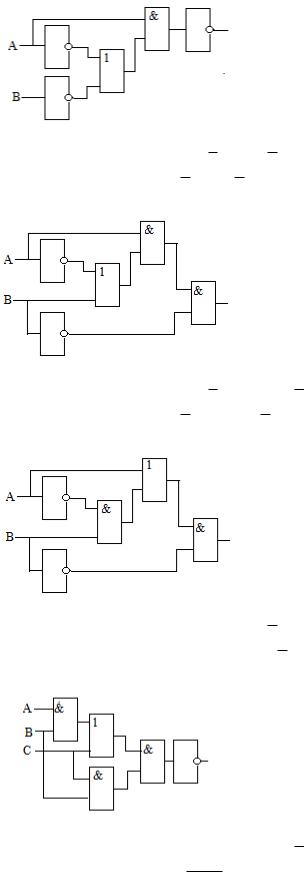
Вариант 21
1.Построить таблицу истинности для формулы В (С А А С) .
2.Построить логическую схему по формуле A B C A.
3.Определить логическую функцию, реализуемую логической схемой
Вариант 22
1.Построить таблицу истинности для формулы В А (С А С) .
2.Построить логическую схему по формуле A B A B .
3.Определить логическую функцию, реализуемую логической схемой
Вариант 23
1.Построить таблицу истинности для формулы А (С А А С) В .
2.Построить логическую схему по формуле ( A B) ( А B) .
3.Определить логическую функцию, реализуемую логической схемой
Вариант 24
1.Построить таблицу истинности для формулы А В (С А А) А .
2.Построить логическую схему по формуле (A B) C D .
3.Определить логическую функцию, реализуемую логической схемой
40
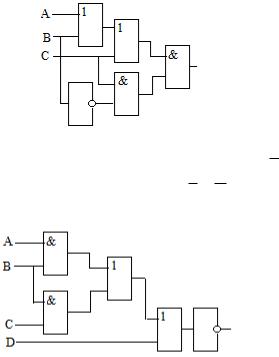
Вариант 25
1.Построить таблицу истинности для формулы В (С А С) В
2.Построить логическую схему по формуле ( A D) (B D) .
3.Определить логическую функцию, реализуемую логической схемой
41
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 4. АЛГОРИТМИЗАЦИЯ
Цель занятия – научиться читать блок-схемы простых алгоритмов.
4.1. Определение алгоритма. Основные алгоритмические конструкции
Алгоритм – понятное и точное указание исполнителю совершать последовательность действий, направленных на решение поставленной задачи. Любой алгоритм можно представить на естественном языке, псевдокоде, алгоритмическом языке или с помощью блок-схемы.
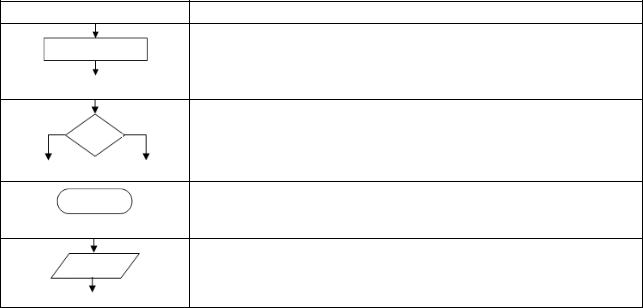
Графические обозначения блоков, которые используются в блок-схеме, стандартизованы. Некоторые из часто используемых блоков приведены в табл.
4.1.
Таблица 4.1
Изображение основных блоков на блок-схеме
Обозначение блока |
Пояснение |
Процесс (вычислительное действие, реализованное операцией присваивания)
Решение (проверка условия, реализующая условный переход)
Начало, конец алгоритма
Ввод исходных данных, вывод результатов
Основные алгоритмические конструкции – следование, ветвление и цикл. Алгоритм, в котором действия выполняются последовательно, одно за дру-
гим, называется линейным (рис. 4.1).
Алгоритм, при выполнении которого порядок следования команд определяется в зависимости от результатов проверки некоторых условий, называют раз-
ветвляющимся.
42
