optics

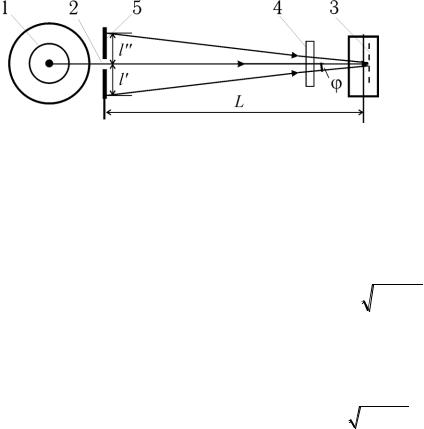
М е т о д и з м е р е н и й

Таким образом, углы дифракции, под которыми наблюдаются максимумы, определяются условием

Здесь m = 0, 1, 2, ...– порядок дифракционного максимума. Из формулы (2) следует, что если падающий свет содержит несколько различных длин волн, то решетка разложит его в спектр (рис. 2б).

В направлении начального распространения света в случае нормального падения( = 0) возникает максимум нулевого порядка (m = 0). Справа и слева от него располагаются сплошные или линейчатые спектры различных порядков (m = 1,2, ...). В каждом из спектров максимумы более коротких длин волн располагаются ближе к центральной полосе.

Если с помощью формулы (2) определяют постоянную ДР, используя монохроматическое излучение с известной длиной волны , то эту операцию называют градуировкой установки. После градуировки такую ДР с известным периодом d можно использовать в качестве спектрометра, т.е. для измерения длин волн

в неизвестном спектре; это выполняют опять-таки с помощью формулы (2).

Оп и с а н и е у с т а н о в к и

Оптическая схема установки показана на рис. 3. Все элементы установки помещаются в стойках на оптической скамье.

Рис. 3. Схема установки: 1 – источник света, 2 – щель,

3 – ДР,

4 – исследуемый светофильтр,

5 – экран Свет от источника, пройдя через щель, попадает на дифракционную решетку.

Дифракционную картину наблюдают непосредственно глазом на экране. Максимум нулевого порядка (центральный) совпадает со щелью. По обе стороны от нее расположены главные максимумы 1-го, 2-го и других порядков. На экране находится отсчетная линейка. Из рис. 3 видно, что

где l – расстояние от щели до максимума с углом дифракции , L – расстояние от экрана до ДР.

Подставляя значение синуса в уравнение (2), получаем

21

П о р я д о к в ы п о л н е н и я р а б о т ы

Задание 1. Исследование линейчатого спектра (определение постоянной дифракционной решетки)

1.На оптическую скамью устанавливаем ртутную лампу, дающую излучение с линейчатым спектром, регулируемую щель и ДР (рис. 3).

2.Включаем лампу, максимально раздвигаем щель и, перемещая щель или ДР в горизонтальном и вертикальном направлениях, добиваемся попадания светового луча на решетку.

!Ртутная лампа сильно нагревается во время работы, а после выключения снова включается только после того, как остынет

3.Наблюдаем через ДР на экране со шкалой дифракционную картину в виде линейчатых спектров. Регулируя расстояние между решеткой и щелью, а также ширину щели, получаем четкое изображение спектров 1-го и 2-го порядков.

4.Измеряем расстояние между дифракционной решеткой и экраном.

5.Определяем положение первой фиолетовой линии в спектрах 1-го и 2-го поряд-

ков, измеряя по шкале расстояния l (влево) и l (вправо) от центрального максимума. Результаты записываем в табл. 1.

6. Аналогичные измерения проводим для других ярких линий спектра ртути Таблица 1

7. По полученным данным для каждой линии спектра рассчитаем среднее расстояние l линии от центрального максимума и постоянную дифракционной решетки d, используя формулу (4). Находим среднее значение величины d.

8. Рассчитаем доверительный интервал (см. приложение 2.1):

10. В выводе отразите назначение и способ осуществления градуировки дифракционного прибора (ДР).

Задание 2. Исследование светофильтра (СФ): определение с помощью ДР его области прозрачности в видимой части спектра.

Часть сплошного спектра, для которой данный фильтр прозрачен, называ-

ют областью прозрачности светофильтра или полосой пропускания.

Для определения области прозрачности СФ находят коротковолновую К и длинноволновую Д границы области, которая находится от К до Д.

1.На оптическую скамью (рис.3) устанавливаем лампу накаливания, дающую сплошной спектр, регулируемую щель (лампа и щель могут быть смонтированы вместе), обойму СФ и ДР. Постоянную дифракционной решетки см. на установке.

2.Включаем лампу, максимально раздвигаем щель и, перемещая щель или ДР

вгоризонтальном и вертикальном направлениях, добиваемся попадания светового луча на решетку.

3.Наблюдаем через ДР на экране со шкалой дифракционную картину в виде сплошных спектров. Регулируя расстояние между ДР и щелью, а также ширину щели, получаем четкое изображение спектров 1-го и 2-го порядков.

4.Выбираем исследуемый СФ и записываем его цвет в табл. 2.

Таблица 2

5.Измеряем и записываем расстояние L между ДР и экраном.

6.В спектре первого порядка определяем положение коротковолновой границы пропускаемого светофильтром света (рис. 4), измерив по шкале с точно-

стью до 1 мм расстояния l (влево) и l (вправо) от центрального max. Результаты измерения заносим в табл. 2.

Рис. 4. Вид спектра лампы накаливания через СФ

7.Находим среднее значение l и по формуле (4) рассчитываем коротковолновую границу спектра пропускания К.

8.Аналогичные измерения и расчеты проводим для спектра 2–го порядка.

Найдем среднее из двух значений К.

9.Проводим измерения по пунктам 6–8 для нахождения длинноволновой границы пропускаемого светофильтром света. Результаты измерений и расчетов также записываем в табл.2.

10.Делаем вывод об области наибольшей прозрачности исследованного СФ и

онаблюдаемых участках пропускания в других областях светового диапазона.

Ко н т р о л ь н ы е в о п р о с ы

1.Какое явление называется дифракцией света?

2.В чем заключается принцип Гюйгенса-Френеля?

3.Каково условие максимума для ДР?

4.Запишите формулу, определяющую положение главных максимумов интенсивности света при дифракции на ДР.

5.Что такое порядок дифракционного спектра?

6.В чем отличие дифракционной картины при наблюдении в монохроматическом и белом свете?

7.Что называют областью прозрачностью фильтра?

Библиографический список

1.Детлаф, А.А. Курс физики / А.А. Детлаф, Б.М. Яворский.– М.: Высш.

школа, 1989. – § 32.1; 32.3–32.4.

2.Трофимова, Т.И. Курс физики / Трофимова Т.И. – М.: Высшая школа,

1994. – §176; 180.

24

Р а б о т а № 5

ИЗУЧЕНИЕ ПОЛЯРИЗАЦИИ СВЕТА

ЦЕЛЬ: исследование поляризации света при отражении от диэлектрика, определение угла полной поляризации. Исследование прохождения света через поляроиды.

ОБОРУДОВАНИЕ: специальная установка, осветитель, вольтметр, линза.

В в е д е н и е

Из электромагнитной теории света следует, что световая волна является поперечной, то есть векторы напряженности электрического поля E , напряжен-

ности магнитного поля H и скорости распространения света c взаимно перпендикулярны. Свет от обычных источников состоит из множества цугов волн, све-

товые векторы E которых ориентированы случайным образом, а колебания различных направлений равновероятны. Такой свет называется естественным.

Свет, в котором направления колебаний каким-либо образом упорярядочены, называется поляризованным, а процесс получения поляризованного света называется поляризацией. Если колебания вектора происходят в одной плоскости относительно луча, то свет считается плоскополяризованным. Частично поляризо-

ванный свет – это свет, в котором имеется преимущественное направление коле-

баний вектора E . Эти случаи схематически показаны на рис.1, где луч перпендикулярен плоскости рисунка.

ся плоскостью поляризации. Поляризация света наблюдается при отражении, преломлении света и при прохождении света через анизотропные вещества. Приборы для получения поляризованного света называются поляризаторами. Поляризованный свет нельзя отличить от неполяризованного визуально. Анализ поляризованного света делают с помощью поляризатора, через который пропускают исследуемый свет. В таких случаях поляризатор называют анализатором.

Для явления поляризации справедливы следующие закономерности.

1. При отражении светового луча от поверхности изотропных диэлектриков, например, от поверхности стекла или воды, отраженный луч оказывается частично поляризованным в плоскости, перпендикулярной плоскости падения. Степень поляризации отраженных лучей меняется при изменении угла падения. Отраженный луч будет плоскополяризован только в том случае, если угол падения имеет определенную величину Бр, называемую углом полной поляризации. Теория и опыт показывают, что угол полной поляризации в этом случае удовлетворяет закону Брюстера

где n – относительный показатель преломления второй среды относительно первой. Таким образом, определив в эксперименте угол Бр , можно найти величину n.

2. Если на анализатор падает плоскополяризованный свет, плоскость поляризации которого составляет угол с плоскостью поляризации лучей, пропускаемых анализатором, то интенсивность пропущенного им света будет опреде-

ляться законом Малюса :

3. Закон Малюса показывает возможность анализа характера и степени поляризации света. Если частично поляризованный свет пропускать через анализа-

тор, то в зависимости от положения плоскости поляризации анализатора

(ППА) будет изменяться интенсивность IA прошедшего света . Она достигает максимального значения Imax если ППА совпадает с плоскостью преимущественных колебаний частично поляризованного света. Если эти плоскости перпендикулярны друг другу, то интенсивность света, прошедшего через поляризатор, будет минимальной Imin.

Для характеристики поляризованного света используют величину, называе-

мую степенью поляризации света P,

Очевидно, что 0 ≤ P ≤ 1. Для естественного света P = 0, так как Imax = Imin, а для плоскополяризованного света P = 1, так как Imin = 0.

О п и с а н и е у с т а н о в к и

26

Для изучения законов Брюстера и Малюса используется специальная установка (рис.2), которая крепится на оптической скамье.

1 – источник света,

2 – поляризатор (П),

3 – стеклянная пластина,

4 – стрелка,

5 – анализатор (А),

6 – шкала анализатора,

7 – фотоэлемент (Ф),

8 – вольтметр,

9 – держатель блока А–Ф,

10 – шкала на корпусе

Рис. 2. Схема установки

Свет от лампы падает на стеклянную пластину, помещенную в защитный корпус. Изменение угла падения света осуществляется поворотом держателя пластин. Красная стрелка на крышке держателя указывает угол падения света. К установке прилагается набор съемных стеклянных пластин, закрепленных в обоймы (по 2, 4, 7, 12 пластин). Отраженный от пластины частично поляризованный свет через анализатор попадает на фотоэлемент, подключѐнный к вольтметру.

ПРИМЕЧАНИЕ: Показания вольтметра U=IФR пропорциональны интенсивности света, попадающего на фотоэлемент (так как фототок IФ пропорционален световому потоку).

Положение плоскости поляризации анализатора отмечают по шкале 6 с помощью указателя. Блок “анализатор – фотоэлемент” (А–Ф) закреплен на держателе, который может поворачиваться вокруг вертикальной оси на угол от 50° до 180°.

Отражающую пластину 3 поворачивают вокруг вертикальной оси. Для отраженного от нее частично поляризованного света плоскость преимущественных колебаний вертикальна. Поэтому на фотоэлемент падает световой поток, зависящий от положения ППА: он будет максимальным (показание вольтметра максимально), если ППА вертикальна, и минимальным, если ППА горизонтальна.

Как следует из теоретических представлений, интенсивность этих двух составляющих Umax и Umin , поляризованных во взаимно перпендикулярных плоскостях, будет изменяться в зависимости от угла падения света в соответствии с графиком, представленным на рис.3.

27

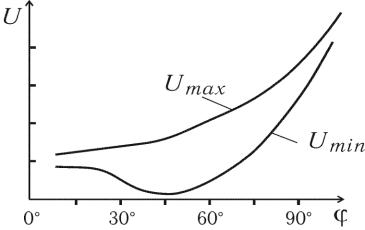
Изменяя угол падения света на пластину и отмечая показания вольтметра, можно най-

ти угол полной поляризации или угол Брюстера.

Рис. 3 Для изучения закона Малюса используют дополнительный поляризатор

(см. рис. 2).

П о р я д о к в ы п о л н е н и я р а б о т ы Подготовка установки к работе

1.Изучите основные узлы и элементы установки и операции с ними: а) блок анализатор-фотоэлемент (А-Ф); б) изменение положения ППА;

в) изменение углов падения и отражения света относительно пластины.

2.Снимите с установки поляризатор и держатель пластин. Включите источник света и, перемещая его вверх-вниз, либо поворачивая, а также перемещая фокусирующую линзу по скамье, добейтесь чтобы световой луч, прошедший через входное отверстие, был симметричен относительно выходного отверстия.

3.Закрепите на держателе обойму с четырьмя пластинами и поставьте его так, чтобы указатель угла поворота был на нулевом делении.

Контроль установки осветителя: пятно отраженного от пластин света должно быть симметрично относительно входного отверстия.

4.Ознакомьтесь с работой анализатора и датчика интенсивности света. Для этого поверните держатель блока анализатора так, чтобы свет, прошедший через пластину, попал на анализатор и фотоэлемент. Включите мультиметр с под-

ключѐнным к нему фотоэлементом. Меняя положение ППА от 0 до 180 , замечайте, что показания мультиметра практически не изменятся.

Следовательно, прошедший через пластину свет – неполяризованный.

5. Повернув отражающую пластину, задайте угол падения света = 30 – 50 , а держатель блока А–Ф поверните в положение 2 . Если в этом случае изменять положение ППА от 0 до 180 , то показания мультиметра будут изменяться от некоторого минимального значения Umin при 0 до Umax при 90 и вновь до

Umin при 180 .

Следовательно, свет, отраженный пластиной, частично поляризован.

28

Задание 1. Исследование поляризации отраженного света

1.Ставим в держатель обойму с четырьмя пластинами и устанавливаем угол падения света =25 .

!При выполнении упражнения необходимо снять поляризатор с оптической скамьи, т.к. поляризация света будет происходить при отражении.

2. Повернув блок А–Ф в положение 2 , записываем в табл.1 показания мультиметра U, пропорциональные интенсивности света, прошедшего через анализатор при двух положениях ППА: при 0 и при 90 .

3.Аналогичные измерения проводим для других углов падения света, указанных в табл.1.

4.Для каждого угла падения рассчитываем степень поляризации отраженно-

го света по формуле (3), подставляя вместо интенсивности света I измеренные значения U.

5. Строим графики зависимостей: Umax=f( ); Umin=f( ) и степени поляризации Р=f( ), по которым находим угол Брюстера.

6.По формуле (1) рассчитываем показатель преломления пластины n.

7.В выводе уместно отразить, как Вы в эксперименте убедились в том, что отраженный от стеклянной пластины свет частично поляризован.

29

Задание 2. Изучение закона Малюса.

1.Снимаем с установки обойму с пластинами; держатель блока А–Ф устанавливаем в положение 180 , а между источником света и установкой помещаем поляризатор 2.

2.Ставим ППА на 0 . Изменяя положение ППП ( ППП) от 0 до 180 через 15 , записываем в табл. 2 показания вольтметра UП (интенсивность света, про-

шедшего через поляризатор и неподвижный анализатор).

3. Ставим ППП на 0 . Изменяя положение ППА ( ППА) от 0 до 180 также через 15 , записываем в табл. 2 показания вольтметра UA (интенсивность света, прошедшего через неподвижный поляризатор и анализатор)

4.Вычисляем среднее значение U для каждого угла .

5.Строим график зависимости U = f (cos2 ).

ПРИМЕЧАНИЕ: При этом аппроксимируем опытную зависимость прямой линией в области более высоких значений U. Затем проводим параллельно опытной теоретическую линию, которая согласно закону Малюса, проходит через точ-

ку (0 , 0).

6. В выводе отражаем способ анализа заведомо поляризованного света и возможные причины систематической погрешности, которая приводит к смещению опытной зависимости относительно теоретической.

30