1.4.3. Мдс фазной обмотки
Пусть
на статоре размещена двухслойная обмотка
с укороченным шагом и 2р=2
(рис. 1.26). Как
показано выше, двухслойная обмотка с
укороченным шагом может быть представлена
как совокупность двух однослойных
обмоток с полным шагом, расположенных
в верхнем и нижнем слоях и сдвинутых
относительно друг друга на угол укорочения
шага
.Такой подход в
данном случае вполне обоснован, так как
величина МДС не зависит от порядка
соединения проводников, а зависит от
тока в проводниках и их размещения. В
результате любую гармонику МДС
двухслойной обмотки с укороченным шагом
можно получить путём сложения
соответствующих гармоник МДС воображаемых
однослойных обмоток. При этом МДС
катушечных групп, лежащих в верхнем и
нижнем слоях, можно представить в виде
пространственных векторов, сдвинутых
на угол
,
определяемый укорочением шага. На рис.
1.26,а показано построение первых гармоник
МДС катушечных групп и фазной обмотки
при
.
Геометрическим сложением векторов,
изображающих МДС катушечных групп,
определяется максимальная амплитуда
первой гармоники МДСобмотки
(см. рис. 1.26,б).
,
где
– коэффициент укорочения для первой
гармоники.
Далее можно записать
,
где
– обмоточный коэффициент.
.
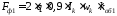В общем случае, когда машина имеет число полюсов 2р, то фазная обмотка состоит из 2р – катушечных групп, которые можно соединить последовательно, последовательно–параллельно и параллельно. При последовательно-параллельном соединении катушечных групп, число последовательно соединённых витков в фазе будет
,
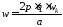где а – число параллельных ветвей;
.
Тогда
или
,
где
– ток фазной
обмотки.
Для
любой
-ой
гармоники МДС фазы максимальная амплитуда
будет
.
Таким образом, МДС фазной обмотки в любой момент времени и в любой точке сдвинутой относительно оси обмотки на расстояние x будет
.
Рассмотрим свойства первой гармоники МДС фазы.
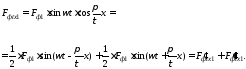
Изобразим
первую составляющую
для двух моментов времени:
и
(рис. 1.27).
Как следует из
построения,
представляет
собой правобегущую волну. Определим
скорость перемещения этой волны, имея
в виду, что для любой фиксированной
точки этой кривой можно принять
или
.
Пр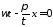и
,
и
или
,
откуда выражение для частоты вращения рассматриваемой прямовращающейся волны получает вид
.
Путём
аналогичного анализа можно доказать,
что вторая составляющая
– является обратновращающейся волной
.
Таким
образом, первую гармонику МДС фазной
обмотки можно представить в виде двух
вращающихся в противоположные стороны
с одинаковой частотой вращения волн.
При этом амплитуда каждой из них равна
половине максимальной амплитуды
пульсирующей волны. Для любой
-ой
гармоники можно написать такое же
выражение, что и для первой гармоники
;
,
.
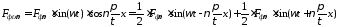Можно
получить тот же вывод методом графического
построения. Первую гармонику пульсирующей
МДС фазы можно представить в виде
пульсирующего пространственного
вектора, изменяющегося в пределах
.
Такой вектора можно заменить двумя
вращающимися векторами. Построим эти
векторы для моментов времени
;
;
(рис. 1.28)
