ОГЛАВЛЕНИЕ

Задача 1…………………………………………………………………………………….3

Задача 2…………………………………………………………………………………….5

Задача 3……………………………………………………………………………………..9

Задача 1 – Плоская система сил

Жесткая рама, расположенная в вертикальной плоскости, закреплена в точке шарнирно, а в точке прикреплена к шарнирной опоре на катках. В точке к раме привязан трос, перекинутый через блок и несущий на конце груз весом кН. На раму действуют пара сил с моментом кН∙м и две силы и . Определить реакции связей в точках и , вызываемые действующими нагрузками. При окончательных подсчетах принять м.

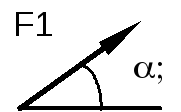
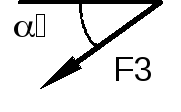
F1= 10 kH		F3= 30 kH
Точка прилож.	град	Точка прилож.	град.
Н	60	Д	30

Исходные данные:

М = 5 кНм

Р = 10 кН

а = 1 м

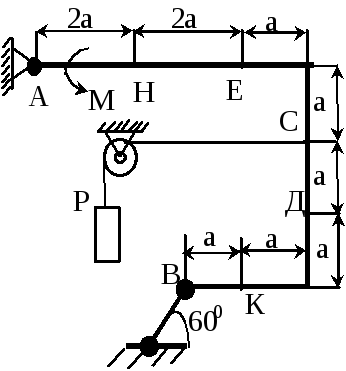
Решение:

Рассмотрим равновесие рамы. Изобразим действующие на раму активные силы: , F3, пару сил с моментом .

Освободим раму от связей, наложенных в точках и , заменив эти связи силами – реакциями. Реакцию неподвижного шарнира , направление которой неизвестно, разложим на две составляющие: горизонтальную и вертикальную . Реакцию невесомого стержня направляем вдоль этого стержня, то есть под углом α = 60º к горизонтали. Натяжение троса направим вдоль троса горизонтально влево, так как трос всегда испытывает только растяжение.

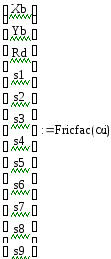
Решение в Mathcad:

Д а н о

Р е ш е н и е

П р о в е р к а

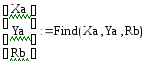
Задача 2 – Плоские стержневые фермы

Определить реакции опор фермы от заданной нагрузки, а также силы во всех ее стержнях способом вырезания узлов.

Номер условий	Узел неподвижной опоры	Узел подвижной опоры
8	II	IV

Исходные данные:

Р₁ = 2кН, Р₂ = 4 кН, Р₃ = 6 кН, а = 2 м, h = 3 м, α = 30 º.

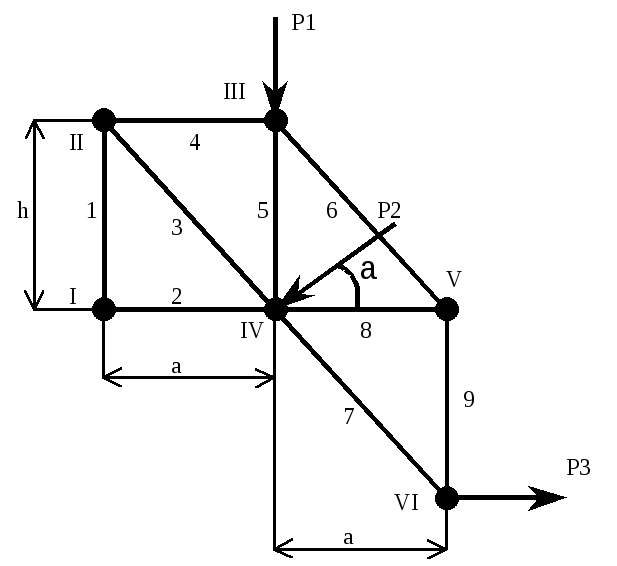
Решение:

Так как по условию задачи в узле II находится неподвижная опора, то реакцию этой опоры представим в виде двух составляющих по координатным осям X_B и Y_B.

В узле I – подвижная опора, поэтому ее реакция направлена вертикально вверх.

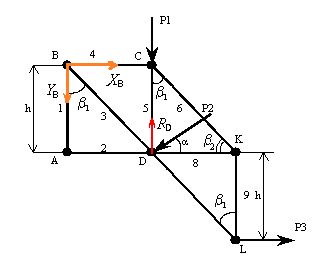
Решение в Mathcad:

Д а н о

Р е ш е н и е

С о с т а в и м с у м м у п р о е к ц и й в с е х с и л н а о с и к о о р д и н а т

С о с т а в и м с у м м у м о м е н т о в в с е х с и л о т н о с и т е л ь н о о с и Z , п р о х о д я щ и х

ч е р е з т о ч к у D.

С о с т а в и м с у м м у м о м е н т о в в с е х с и л о т н о с и т е л ь н о о с и Z , п р о х о д я щ и х

ч е р е з т о ч к у D.

Задача 3 – Пространственная система сил

Две однородные прямоугольные тонкие плиты жестко соединены (сварены) под прямым углом друг к другу и закреплены сферическим шарниром в точке , цилиндрическим подшипником в точке и невесомым стержнем 1, который прикреплен к плите и к неподвижной опоре шарнирами.

Размеры плит указаны на рисунке; вес большей плиты кН, вес меньшей плиты

Р₂ = 10 кН. Большая плита параллельна вертикальной плоскости , меньшая плита расположена в вертикальной плоскости .

На плиты действуют пара сил с моментом М = 5 кНм, лежащая в плоскости большей плиты, и две силы. Значения этих сил, их направления и точки приложения заданы.

Определить реакции связей в точках и и реакцию стержня. При подсчетах принять а = 1 м.

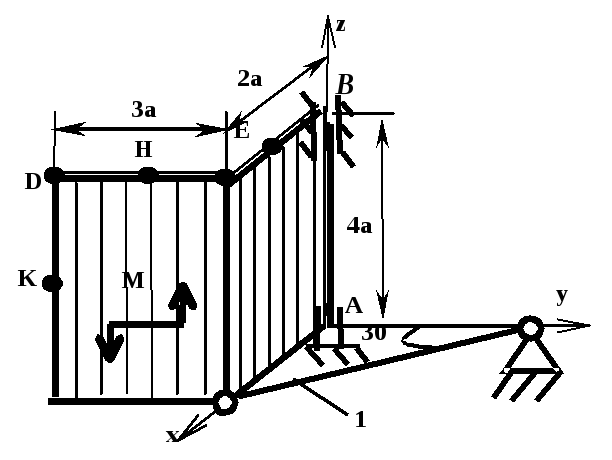
Исходные данные: м; кН; Р₂ = 10 кН; М = 5 кНм; кН; точка приложения – ; кН; точка приложения – ; . Угол стержня 1 с осью равен 0º.

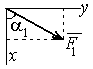
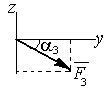
Решение:

Рассмотрим равновесие конструкции, состоящей из двух однородных прямоугольных тонких плит, сваренных под прямым углом друг к другу. На конструкцию действуют заданные силы и , веса плит и , пара с моментом , а также реакции связей. Реакцию сферического шарнира разложим на три составляющие ; цилиндрического подшипника – на две составляющие (в плоскости перпендикулярной оси подшипника – ось ); реакцию стержня направляем вдоль стержня, предполагая, что он растянут (стержень 1 находится в плоскости xy параллельно оси y).