Практичне заняття №7
ПЕРЕДАЧА ІНФОРМАЦІЇ ЧЕРЕЗ КАНАЛ З ПЕРЕШКОДАМИ
7.1 Мета заняття
Метою заняття є ознайомлення студентів з методами кодування, що застосовуються у системах передачі дискретної інформації за умов наявності перешкод.
7.2 Методичні вказівки для самостійної підготовки до заняття [2,3,6].
При передачі інформації через канал з перешкодами повідомлення можуть зазнавати викривлень, тому й на прийомній стороні немає повної впевненості в тім, що прийнято саме те повідомлення, яке передавалося. Отже, імовірність достовірності такого повідомлення після прийому не дорівнює одиниці.
У цьому випадку кількість
отриманої інформації зменшується на
величину невизначеності, внесеною
перешкодами, тобто визначається як
різниця ентропії повідомлення до та
після прийому:
,
де
- ентропія джерела повідомлень;
- ентропія повідомлень на прийомній
стороні. Зменшення кількості отриманої
інформації внаслідок дії перешкод
розглянемо на прикладі передачі
повідомлень про стан двохпозиційного
контрольованого об'єкта (включено,
виключено).
Нехай імовірності включеного
та виключеного станів відповідно
дорівнюють:
.
Імовірність того, що при передачі стану
«виключено» приймається інформація
про включений стан,
.
Відповідно інші умовні ймовірності
дорівнюють:
;
;
,
де
- умовна ймовірність того, що при передачі
повідомлення
буде прийнято повідомлення
.
За таких умов ентропійні характеристики
мають наступні значення:
;
.
Таким чином, за рахунок дії
перешкод кількість інформації зменшується:
[біт].
Розділивши
на час
передачі одиночного повідомлення,
отримаємо формулу для швидкості передачі
інформації по каналу зв'язку з перешкодами:
|
|
(7.1) |
.Пропускною здатністю каналу із шумами називається максимальна швидкість передачі інформації на символ або в одиницю часу за умови, що канал зв'язку без перешкод погоджено із джерелом інформації:
|
|
(7.2) |
.
Якщо ентропія джерела
інформації не перевищує пропускної
здатності каналу
,
то існує код, який забезпечує передачу
інформації через канал з перешкодами
з як завгодно малою частотою помилок
або як завгодно малою невірогідністю.
Введемо визначення пропускної здатності
каналу зв'язку при обмеженій середній
потужності аналогового сигналу:
|
|
(7.3) |
,
де 
- смуга частот каналу;
- середня потужність сигналу;
- середня потужність перешкод (рівномірний
спектр) з нормальним законом розподілу
амплітуд у смузі частот каналу зв'язку.
Отже, можна передавати інформацію по каналу з перешкодами без помилок, якщо швидкість передачі інформації
|
|
|
.
Для швидкості
при будь-якій системі кодування частота
помилок обмежена, причому вона швидко
зростає зі збільшенням
.
Очевидно, що для каналу з
високим рівнем шумів
максимальна швидкість передачі є
близькою до нуля. В той же час при
.
Максимальна кількість інформації, яка
передається за час
,
називається об'ємом сигналу
|
|
|
.
Одними з найпоширеніших систематичних кодів, що використовують у системах передачі іформації через канали з перешкодами, є коди Хемінга .
До них звичайно відносять
коди з мінімальною кодовою відстанню
,
які виправляють всі одиночні помилки,
і коди з відстанню
(кодова відстань між двома кодовими
комбінаціями – число однойменних
розрядів з різними символами), які
виправляють всі одиночні й виявляють
всі подвійні помилки. Довжина коду
Хемінга
|
|
(7.4) |
,де
- кількість перевірочних розрядів.
З нерівності (7.4) отримуємо
|
|
(7.5) |
.
Формулу (7.5) можна привести до наступного виду:
|
|
(7.6) |
,де
- кількість інформаційних розрядів.
Ця нерівність дозволяє визначити довжину коду при заданому числі інформаційних розрядів. У табл. 7.1 наведено параметри деяких кодів Хемінга.
Таблиця 7.1 Параметри кодів Хемінга
|
|
|
|
|
|
|
|
|
|
|
|
4 |
3 |
7 |
0,429 |
3 |
4 |
4 |
8 |
0,5 |
4 |
|
11 |
4 |
15 |
0,267 |
3 |
11 |
5 |
16 |
0,312 |
4 |
|
26 |
5 |
31 |
0,161 |
3 |
26 |
6 |
32 |
0,188 |
4 |
|
57 |
6 |
63 |
0,095 |
3 |
57 |
7 |
64 |
0,109 |
4 |
|
120 |
7 |
127 |
0,055 |
3 |
120 |
8 |
128 |
0,063 |
4 |
|
247 |
8 |
255 |
0,031 |
3 |
247 |
9 |
256 |
0,035 |
4 |
|
502 |
9 |
511 |
0,0177 |
3 |
502 |
10 |
512 |
0,0195 |
4 |
|
1013 |
10 |
1023 |
0,0098 |
3 |
1013 |
11 |
1024 |
0,0107 |
4 |
Характерною рисою перевірочної
матриці коду з
є те, що її стовпці містять різні ненульові
комбінації довжиною
.
Наприклад, при
й
,
тобто для коду
,
перевірочна матриця може мати такий
вигляд:
|
|
|
.Перестановкою стовпців, які містять одну одиницю, дану матрицю можна привести до виду
|
|
|
.Використання такого коду дозволяє виправити будь-яку одиночну помилку або виявити довільну помилку кратності два.
Якщо інформаційні й перевірочні розряди коду нумерувати зліва направо, то відповідно до матриці отримуємо систему перевірочних рівнянь; за допомогою яких обчислюємо перевірочні розряди:
|
|
(7.7) |
;
;
;
,де
-
- перевірочні розряди;
-
- інформаційні розряди.
У тому випадку, коли при
передачі кодового слова виникає одиночна
помилка, виявляються ненульовими ті
перевірочні співвідношення, у які
входить значення помилкового розряду.
Наприклад, якщо помилка виникла в п'ятому
інформаційному розряді, виявляться
ненульовими перше й четверте рівняння,
тобто синдром дорівнює 1001 (збігається
з п'ятим стовпцем матриці
).
Звідси отримуємо алгоритм визначення
одиночної помилки: місце розташування
стовпця матриці
,
що збігає з обчисленим синдромом, вказує
місце помилки. Ясно, що обчислене значення
синдрому обов'язково збігається з одним
зі стовпців матриці
,
тому що як стовпці обрано всі можливі
двійкові
-
розрядні числа.
Хемінг запропонував
використовувати таке розташування
стовпців перевірочної матриці, щоб
номер
-го
стовпця матриці й номер розряду кодової
комбінації відповідав двійковому
уявленню числа
.
У цьому випадку синдром, який отримано
з перевірочних рівнянь, є двійковим
представленням номера розряду комбінації,
у якому відбулася помилка. Для цього
перевірочні розряди повинні знаходитися
не наприкінці кодової комбінації, а на
номерах позицій, які відображуються
ступенем двійки (
), тому що кожний з них входить тільки
до одного з перевірочних рівнянь.
Таким чином, перевірочні
рівності для коду Хемінга
мають вигляд:
|
|
(7.8) |
;
;
;
,а перевірочна матриця
|
|
|
.
Приклад 7.1
Для
,
у якості перевірочної може бути обрана
наступна матриця:
|
|
|
.
Як перевірочні розряди
вибираємо перший, другий і четвертий.
Щоб закодувати повідомлення 1310=11012,
необхідно визначити перевірочні розряди
в комбінації
.
З матриці
маємо
;
;
.
Отже,
,
,
і закодоване повідомлення має вигляд
1100110 (рис.7.1а).
Припустимо, що шостий символ прийнятий
помилково, тоді буде отримане повідомлення
1000110. Синдром у цьому випадку має значення
110, що двійковому представленню числа
6 (рис.7.1б).
Двійковий код Хемінга з
кодовою відстанню
утворюється шляхом додавання до коду
Хемінга з
одного перевірочного розряду, який
представляє собою результат підсумовування
по модулю два всіх розрядів кодового
слова, у такий спосіб формується
модифікований код Хемінга. Довжина коду
при цьому
розрядів, з яких
є перевірочними.
Операція кодування може
виконуватися у два етапи. На першому
етапі визначається кодова комбінація
з використанням матриці
,
що відповідає коду з
,
на другому - додається один перевірочний
розряд, у якому записується результат
підсумовування по модулю для всіх
розрядів кодового слова, яке отримано
на першому етапі.
|
|
|
|
а) |
б) |
|
Рис. 7.1 Формування коду Хемінга | |
Операція декодування також
складається із двох етапів. На першому
обчислюється синдром, що відповідає
коду з
,
на другому перевіряється останнє
перевірочне співвідношення. Результати
виконання цих операцій і відповідні їм
висновки наведено у табл. 7.2
Таблиця 7.2 Таблиця аналізу результатів декодування
|
Синдром |
Додаткове контрольне співвідношення |
Висновки |
|
Не дорівнює нулю |
Виконується |
Відбулася подвійна помилка |
|
Не дорівнює нулю |
Не виконується |
Відбулася одиночна помилка |
|
Дорівнює нулю |
Виконується |
Помилок немає |
|
Дорівнює нулю |
Не виконується |
Відбулася потрійна або більше високої кратності, але непарна помилка |
Перевірочна матриця для (16,
11)-коду з
може мати вигляд:
|
|
|
.
Додаткове перевірочне співвідношення, що вводиться для збільшення мінімальної відстані коду Хемінга, представимо так:
.
З урахуванням (7.8) отримуємо
Система рівнянь (7.8) і останнє
співвідношення для
дозволяє записати перевірочну матрицю
для коду (16, 11):
|
|
(7.9) |
Іноді при практичному
використанні коду вирішують задачу
одержання скороченого коду із заданою
мінімальною відстанню (
або 4). У цьому випадку будується
перевірочна матриця для з коду з найменшим
значенням
,
яке задовольняє наступним умовам:
|
|
(7.10) |
|
|
(7.11) |
,
для коду з
;
,
для коду с.
У другому випадку число
перевірочних розрядів коду дорівнює
.
Потім в отриманій матриці відкидаються
усі зайві стовпці підматриці
.
Приклад 7.2
Побудувати перевірочну матрицю для
коду Хемінга
,
який містить
інформаційних розрядів.
Найменше значення
,
що задовольняє нерівності (7.11), дорівнює
4.
Довжина коду дорівнює 16. Матрицю для цього коду наведено в (7.9). У підматриці, яка містить 11 розрядів, викреслюємо останній стовпець для економії апаратури (звичайно викреслюють стовпці з найбільшою кількістю одиниць).
Перевірочна матриця скороченого коду (15,10) у цьому випадку має вигляд
|
|
|
Вагову характеристику коду
Хемінга зручно знаходити за допомогою
функції
,
яка дозволяє визначити число кодових
векторів з різними вагами.
Для коду з
|
|
(7.12) |
.
Для коду з
|
|
(7.13) |
.
У формулах (7.12), (7.13) число
кодових векторів ваги
дорівнює значенню коефіцієнтів
багаточлена, що стоять перед
.
Приклад 7.3
Нехай задано код Хемінга с
.
Визначити коефіцієнти помилкових
переходів. Для цього коду відповідно
до формули (7.11) маємо
|
|
|
Отже, даний код містить одне
кодове слово ваги 0, сім слів ваги 3, сім
слів ваги 4 і одне слово ваги 7. Це значить,
що розподіл робочих векторів по кодових
відстанях для даного коду є наступним:
;
,
,
.
Коефіцієнти помилкових переходів
дорівнюють:
;
;
;
.
Тому цей код виявляє всі одно-, двох-, п'яти-, шести - кратні помилки та 80% трикратних і чотирикратних помилок.
7.3 Задачі для самостійної роботи
7.3.1Побудувати
груповий код Хемінга з виявленням
подвійної й виправленням одиночної
помилки для заданого числа
та виправити помилку в зазначеному
розряді (варіанти завдань представлено
в табл. 7.3).
Таблиця 7.3 Варіанти завдань
|
№ варіанта |
Число
|
Помилковий розряд |
№ варіанта |
Число
|
Помилковий розряд |
|
1 |
1025 |
1 |
16 |
456 |
15 |
|
2 |
2015 |
15 |
17 |
354 |
14 |
|
3 |
1999 |
14 |
18 |
1789 |
13 |
|
4 |
253 |
2 |
19 |
777 |
12 |
|
5 |
795 |
7 |
20 |
324 |
11 |
|
6 |
346 |
6 |
21 |
420 |
10 |
|
7 |
1287 |
4 |
22 |
891 |
9 |
|
8 |
235 |
5 |
23 |
359 |
8 |
|
9 |
1474 |
3 |
24 |
643 |
7 |
|
10 |
2040 |
9 |
25 |
782 |
6 |
|
11 |
1244 |
10 |
26 |
465 |
5 |
|
12 |
2047 |
12 |
27 |
698 |
4 |
|
13 |
788 |
8 |
28 |
712 |
3 |
|
14 |
123 |
13 |
29 |
346 |
2 |
|
15 |
568 |
11 |
30 |
289 |
1 |
7.3.2 Знайти та виправити помилку у прийнятій двійковій комбінації коду Хемінга (варіанти завдань наведено у табл. 7.4).
Таблиця 7.4 Варіанти завдань
|
№ варіанта |
Кодова комбінація | ||||||||||||||
|
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 | |
|
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
|
2 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
|
3 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
4 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|
5 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
|
6 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
7 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
8 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
9 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
10 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
11 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
|
12 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
|
13 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
14 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
15 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
|
16 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
17 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
|
18 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
19 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
|
20 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
21 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
22 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
|
23 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
24 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
25 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
|
26 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
|
27 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
28 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
29 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
|
30 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
7.4 Контрольні запитання і завдання
1 Як обчислюється швидкість передачі інформації через дискретний канал з перешкодами?
2 Як визначається пропускна здатність дискретного каналу з перешкодами?
3 У чому полягає сутність теореми Шеннона для дискретного каналу з перешкодами?
4 Поясніть характер залежності пропускної здатності неперервного каналу з перешкодами від смуги пропущення каналу.
5 Які коди називають коригувальними?
6 Як визначається відстань між кодовими комбінаціями?
7 Що розуміється під кодовою відстанню?
8 Висвітлити методику побудови коду Хемінга?
9 У чому полягає логіка декодування Хемінга?
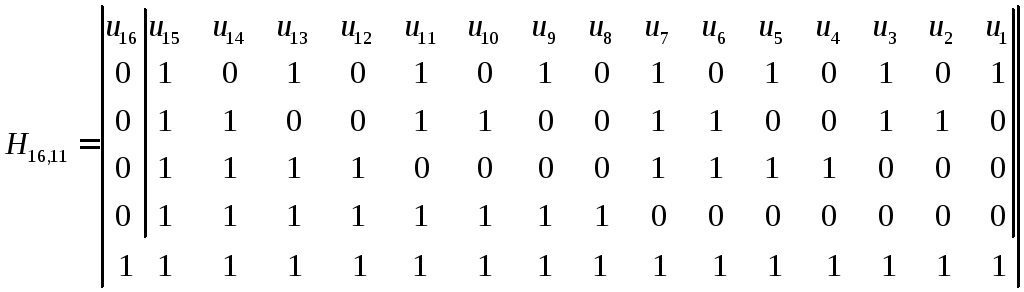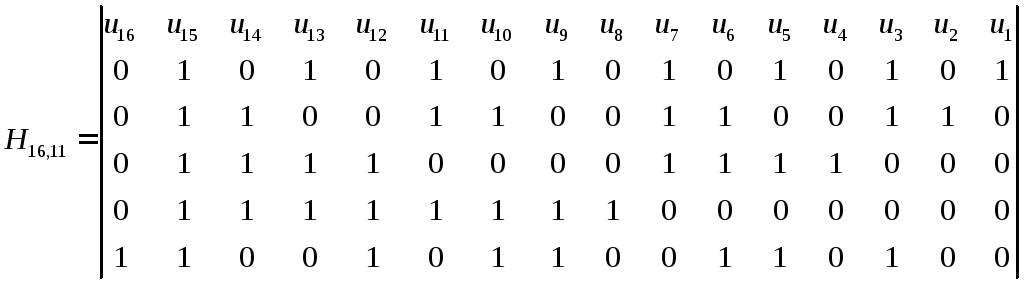