ChM / ChM

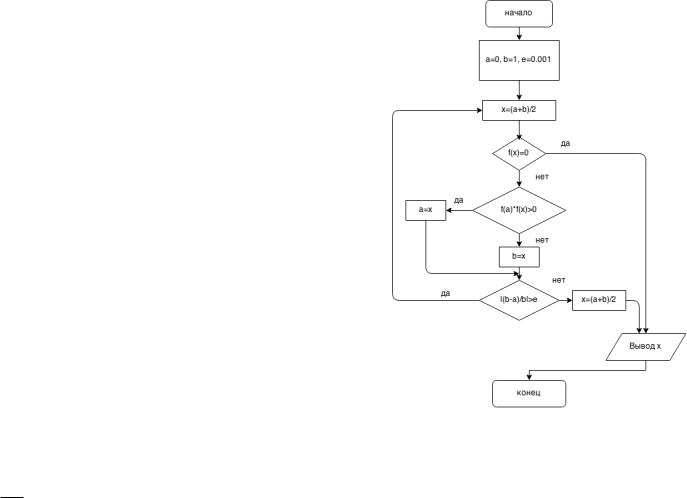
•3. 1 â. Определить все корни уравнения ex + x3x 4 = 0, îäèí èç êîð-

íèÿ f(x) = 0 находится на отрезке [0; 1]. Äëÿ

уточнения корня используем метод половинного деления, суть которого состоит в делении отрезка [a; b], на котором находится корень,

пополам, то есть вычислении = a+2 b, è âûáî- ре того из полученных отрезков, на концах которого функция принимает значения разных знаков. Таким образом процесс продолжается до тех пор, пока в точке деления не получим значений функции равное нулю, или пока отрезок не станет достаточно малым, чтобы любую его точку можно было считать приближенным значением корня уравнения. Чтобы

получить значение корня с точностью ", длина отрезка должна быть не больше ". Но нам необходимо получить значение корня с точностью до двух верных

значащих цифр, поэтому условием выхода из процесса деления является условиеb ba < ", ãäå a; b текущие концы отрезка, " = 0:001.

Результатом работы программы является приближенное значение корня уравнения xp:d = 0:321044921875, значение f(xp:d) 0:001536. Решив это же урав-

нение методом хорд, получили xh = 0:32063463272303333, f(xh) 0:005324.

То есть приближенное значение корня данного уравнения с точностью до двух значащих цифр равно 0:321. Метод половинного деления проще и в данной зада-

че выдал приближенное значение корня ближе к настоящему, так как значение функции в нем меньше по модулю, чем в методе хорд, при аналогичном контроле точности. Вычислительная мощность современных компьютеров настолько велика, что работа программы заняла не более миллисекунды.

Абрамова О.П. Методические рекомендации к практикуму по методам вычислительной математики (для студентов специальностей 01.01 и 01.02) // О.П. Абрамова, Е.В. Алтухов, М.Д. Гремалюк, В.Г. Житняя, Н.М. Нескородев, Л.Н. Шкодина Донецк: ДонГУ, 1990. 80 с.

•3. 14 â. Определить все корни уравнения xe x e 2 = 0, один из корней

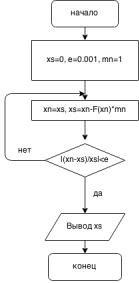
цию метода Ньютона. Суть обычного метода Ньютона заключается в последовательíûõ приближениях к корню по формуле xn+1 = xn f0(xn) x0 = a, åñëè

f (xn), причем

f(a)f00(a) > 0 è x0 = b, åñëè f(b)f00(b) > 0. В нашем

случае a = 0, b = 1, f00(x) = e x (1 x)e x = (x

2)e x, f00(0)f(0) > 0, значит x0 = a = 0. В обычном ме-

тоде Ньютона неудобством является необходимость0 для каждого шага пересчитывать значение 1=f (xn). Òàê êàê

f0 непрерывна и не обращается в нуль в окрестности решения, можно считать

подходит. Но и корень строго меньше b = 1. Поэтому можно считать, что b < 1,

тогда m1 = ". Грубая прикидка дает M2 = 2, поэтому условием выхода из цикла будет xn+1 xn < ".

xn+1

Результатом работы программы является приближенное значение корня урав-

нения xmN = 0:15855649384844123, значение f(xmN ) 0:000027. Решив это

же уравнение обычным методом Ньютона, получили xN = 0:15859433956289492, f(xh) 1:0372258607560525 10 13. То есть приближенное значение корня дан-

ного уравнения с точностью до двух значащих цифр равно 0:159. Модифициро-

ванный метод Ньютона требует меньшего количества вычислений, зато обычный дает более быструю сходимость и большую точность, так как значение функции в нем меньше по модулю, чем в модифицированном методе при аналогичном контроле точности. С другой стороны, вычислительная мощность современных компьютеров настолько велика, что работа программы для обеих методов заняла очень мало времени.

Абрамова О.П. Методические рекомендации к практикуму по методам вычислительной математики (для студентов специальностей 01.01 и 01.02) // О.П. Абрамова, Е.В. Алтухов, М.Д. Гремалюк, В.Г. Житняя, Н.М. Нескородев, Л.Н. Шкодина Донецк: ДонГУ, 1990. 80 с.

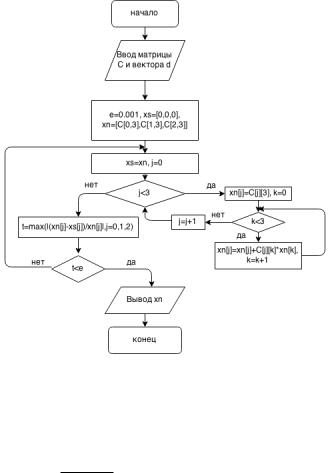
Метод итераций решения системы уравнений Ax = b состоит в последователь-

ном приближении к решению при помощи формулы xn+1 = Cxn +d, где матрица

C и вектор d получаются преобразованием исходной системы к виду x = Cx + d.

При этом на главной диагонали C äîëæ-

ны стоять нули. Итерационный процесс будет гарантированно сходящимся, если сумма квадратов элементов матрицы C

будет меньше единицы. Поэтому, чтобы получить матрицу C и вектор d, íóæ-

но переставить строки исходной системы так, чтобы на главной диагонали оказались самые большие по модулю числа в этой строке, затем поделить каждое уравнение на соответствующие числа, и пере-

нести все, кроме соответствующих переменных, в правые части. За первое приближение можно взять вектор d. В методе Зейделя при вычислении координат век-

y= 3:55653, z = 2:16763, найденное по методу простых итераций и x = 1:91085,

y= 3:56113, z = 2:17306, найденное по методу Зейделя. Метод Зейделя по срав-

нению с методом простых итераций да¼т более быструю скорость сходимости, то есть уменьшение количества вычислений, хотя, имея современные компьютеры, убедиться в этом очень сложно, поскольку все вычисления происходят почти мгновенно. Тестирование на современном смартфоне также не показало разницы во времени вычислений. Недостатком метода является необходимость приведения исходной системы к определенному виду. Даже попытки вручную свести исходную систему путем эквивалентных преобразований к виду x = Cx+d, где элементы C

удовлетворяет указанным выше условиям, не увенчались успехом, не говоря уж о программировании этого процесса.

Абрамова О.П. Методические рекомендации к практикуму по методам вычислительной математики (для студентов специальностей 01.01 и 01.02) // О.П. Абрамова, Е.В. Алтухов, М.Д. Гремалюк, В.Г. Житняя, Н.М. Нескородев, Л.Н. Шкодина Донецк: ДонГУ, 1990. 80 с.

http://tpdn.ru/library/articles/52/14014