Раздел3. Стратегия развития предпринимательства украины

3.1 Моделирование и прогнозирование основных показателей предпринимательской деятельности в Украине

Конституция Украины закрепляет предпринимательство как важнейшее право человека и гражданина Согласно ей (ст.42) каждый имеет право на предпринимательскую деятельность, не запрещенную законом, а государство обеспечивает защиту конкуренции в этой сфере (ст.42), исключительно законами определяет гарантии и правовые основы предпринимательства (п,8 ст.91). [12]

На сегодняшний день формирование эффективной, конкурентоспособной, социально-ориентированной экономики составляет стратегический курс государственной политики Украины.

Для оценки ситуации сектора предпринимательской деятельности и его дальнейшего становления необходимо подобрать оптимальную модель развития основных показателей, а также спрогнозировать дальнейшие изменения в предпринимательской деятельности.

Среди разнообразных моделей, используемых для определения эффективности использования ресурсов, наилучшей с точки зрения математической интерпретации и экономического содержания была выбрана модель производственной функции, т.е. функция Кобба-Дугласа. Поскольку исходные данные представляют собой ряды динамики, то в модель производственной функции был включен фактор времени, модифицируя классическую модель производственной функции [21].

Алгоритм моделирования и прогнозирования модифицированной модели производственной функции идентичен алгоритму степенной динамической корреляционно-регрессионной модели, который включает несколько этапов [21]:

- обоснование наличия стохастической зависимости между факторными и результативным признаками модели;

Признакам наличия стохастической связи является соответствие каждого значения факторного признака множеству значений результативного признака. В данном случае как на факторные признаки (капитальные инвестиции; фонд оплаты труда; время), так и на результативный признак (объем реализованной продукции) воздействуют случайные факторы, что свидетельствует о независимости признаков и, как следствие, о наличии стохастической связи между ними.

- выбор системы факторных признаков для включения в регрессионную модель в качестве независимых переменных;

Для выбора факторных признаков для включения в регрессионную модель в качестве независимых переменных была построена матрица парных коэффициентов корреляции, в которую были включены следующие 3 факторных и 1 результативный признак:

1. Валовые капитальные инвестиции в предпринимательство, млрд. грн.(К)

2. Численность занятых работников на предприятиях (тыс. чел.), (L)

3. Время (t)

4. Объем реализации продукции (работ, услуг) субъектами предпринимательства, млрд. грн. (Y)

Данные для построения модели эффективности использования ресурсов субъектов предпринимательства представлены в таблице 3.1

Матрица парных коэффициентов корреляции (табл. 3.2) позволяет сделать вывод о тесноте связи факторов с результативным признаком и между собой, а также выбрать наиболее значимые факторы для включения в уравнение регрессии.

Таблица 3.1 Исходные данные для построения модели эффективности использования ресурсов предприятий Украины

Годы	Объем реализованной продукции (работ, услуг) предприним- ательства. млрд.грн. (Y)	Валовые капитальные инвестиции в предпринимательство, млрд грн (К)	Численность занятых работников на предприятиях (тыс.чел) % (L)	t
2004	1405,096	101.28	9581,7	5
2005	1514 549	106,179	9429,9	6
2006	1898,295	142,487	9272,5	7
2007	2414,715	205,063	9154,3	8
2008	3014,742	245,981	8969,4	9
2009	3102,361	190,839	8501,3	10
2010	3462,136	129,914	8186	11
2011	4091,411	191.314	8022,1	12
2012	4307,146	229,325	7920,9	13

Полученная матрица парных коэффициентов корреляции свидетельствует о наличии тесной прямой связи между объемом реализованной продукции и объемом капитальных инвестиций в предпринимательство ( ), а также между объемом реализованной продукции и численностью занятых работников на предприятиях, которые занимаются предпринимательской деятельностью (), о чем свидетельствуют парные коэффициенты корреляции выше 0,8. Связь между объемом реализованной продукции и временем заметная и прямая ().

Таблица 3.2 Матрица парных коэффициентов корреляции

	Y	К	L	t
Y	1
К	0,864	1
Ь	0,862	0,826	1
t	0,675	0,544	0,879	1

Несмотря на наличие мультиколлинеарности между факторами L и t ), фактор времени не может быть исключен исходя из метода построения динамических корреляционно-регрессионных моделей.

- проверка наличия всех требований, предъявляемых к факторным признакам при корреляционно-регрессионном анализе;

- однородность распределения: Однородность распределения единиц совокупности имеет место, когда коэффициенты вариации не превышают 33%.

Рассчитаем коэффициент вариации для фактора К:

Аналогично получаем коэффициенты вариации для факторов L, t и Y:

Поскольку коэффициенты вариации факторов К и t превышают пороговое значение 33%, то можно сделать вывод о статистической неоднородности совокупности. Однако, исходя из общих принципов формирования совокупности, данную совокупность можно считать однородной и пригодной для дальнейшего анализа.

- соответствие нармальному закону распределения:

Для проверки соответствия нармальному закону распределения используется правило «трех сигм». По правилу «трех сигм» были определены интервалы:

а) для факторных признаков K,L и t:

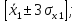
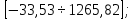
Поскольку принадлежат интервалуто с вероятностью 0,997 можно утверждать, что факторный признак К соответствует нормальному закону распределения.

Аналогично находим интервал для фактора L [-108,95 1218,48] при

Поскольку принадлежат интервалу [-7,8228,43], то с вероятностью 0,997 можно утверждать, что факторный признакL соответствуют нормальному закону распределения.

Интервал для фактора t имеет вид:[-2 10] при. Посколькупринадлежат интервалу [-210], то с вероятностью 0,997 можно утверждать, что факторный признакX3 соответствует нормальному закону распределения.

б) для результативного признака Y:

Поскольку принадлижат интервалуто с вероятностью 0,997 можно утверждать, что результативный признак Y соответствует нормальному закону распределения.

- определить уравнение регрессии модели модифицированной производственной функции;

Уравнение регрессии модели модифицированной производственной функции имеет вид:

Параметры являются частными коэффициентами эластичности, характеризующие связь между объемомреализованной продукции, валовыми капитальными инвистициями, численностью занятых в предпринимательстве и временем. Параметр показывает, что объем реализованной продукции в среднем увеличится на 0,168% при увеличении объема валовых капитальных инвестиций на 1% при условии, что факторыL и t (численность занятых и время) не варьируют, т.е. зафиксированы на среднем уровне. Параметр показывает, что объем реализованной продукции предпринимательства в среднем увеличится на 0,738% при увеличении численности занятых в предпринимательства на 1% при условии, что факторыK и t (валовые капитальные инвестиции и время) зафиксированы на среднем уровне. В среднем ежегодно объем реализации увеличивался на 0,124%, что во многом обусловлено влиянием инфляционных процессов (т. к. объем реализации- в фактических ценах).

Соотношение параметров и () свидетельствует о формирующемся в предпринимательстве капиталозатратном и трудоинтенсивном типе производства.

Поскольку сумма параметров модели (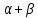=0,906) меньше единицы, то имеет место деинтенсивный тип производства, проявляющийся в недостаточно эффективном использовании ресурсов, что обусловливает необходимость принятия таких управленческих решений, которые бы позволили улучшить данные параметры в целом по всем предприятиям, занимающимся предпринимательской деятельностью.

Преобразование уравнения репрессии в стандартизированный вид было выполнено на основе степенной регрессии. Для этого было произведено преобразование коэффициентов регрессии в сравнимые показатели путем стандартизации переменных. Стандартизированные коэффициенты , ибыли найдены следующим образом:

Тогда уравнение многофакторной степенной регрессии в стандартизированном выражении будет иметь вид:

Параметр () уравнения моногофакторнрой степенной регрессиив стандартизированном выражении подтверждает наличие в предпринимательстве капиталозатратного и трудоинтенсивного типа производства

После ввода переменных Z1 (Z1=К*t) и Z2 (Z2=L*t) в исходную область значений, уравнение многофакторной линейной регрессии будет иметь вид:

Положительные параметры при факторах Z1и Z2 свидетельствуют о наличии и положительной динамики к росту объема капитальных инвестиций численности занятых во времени.

-рассчитать показатели теснты связи;

Количественной мерой зависимости вариации результативного фактора от всех факторных признаков, входящих в уравнение регрессии, является множественный коэффициент корреляции ().

Множественный коэффициент корреляции показал, что зависимость между объемом реализовано продукции, объемом капитальных инвестиций, численности занятых и временем тесная.

Множественный коэффициент детерминации показал что вариация объема реализованной продукции на 75,8% обусловлена вариацией объема валовых капитальных инвестиций, численностью занятых и временем, а на 24,2% - не включенными в модель факторами.

Поскольку множественный коэффициент корреляции и множественный коэффициент детерминации зависят, в свою очередь, от размера совокупности (n) и количества факторных признаков (m), то для определения более точной меры зависимости были рассчитаны скорректированные множественный коэффициент корреляции и множественный коэффициент детерминации, скорректированные на число степеней свободы.

Для характеристики зависимости между результативным фактором и отдельным факторным признаком при условии элиминирования влияния всех остальных факторов, входящих в уравнение регрессии, были рассчитаны частные коэффициенты корреляции и детерминации.

Частные коэффициенты корреляции о наличии тесной и прямой связи между объемом реализованной продукции (работ, услуг) и объемом валовых капитальных инвестиций при условии элиминирования факторов L и t. Между объемом реализованной продукции и численностью занятых в предпринимательстве имеет место тесная и прямая связь при условии элиминирования факторов К и t, а между объемом реализованной продукции предприятий и временем имеет место заметная и прямая связь при условии элиминирования факторов К и L.

Найденные частные коэффициенты детерминации характеризуют долю вариации объема реализованной продукции, дополнительно объясняемой при включении фактора К (L или t), в величине вариации Y, не объясняемой ранее включенными факторами.

Для оценки роли каждого отдельного фактора в формировании вариации результативного фактора под влитием всех факторов, включенных в модель, были рассчитаны коэффициенты раздельной детерминации.

;

Показатели раздельной детерминации показывали, что на 43,6% вариация объема реализованной продукции непосредственно обусловлена вариацией вловых капитальных инвестиций, на 34,8% - вариацией численности занятых в предпринимательстве, а на 3% - вариацией фактора времени.

Таким образом, сумма коэффициентов раздельной детерминации равна множественному линейному коэффициенту детерминации.

- проверка статистической достоверности модели (уравнения связи, параметров уравнения связи и показателей тесноты связи);

На основе полученной модели модифицированной производственной функции с помощью пакета прикладных программ «Анализ данных» MS Ехсеl были рассчитаны несколько критериев аппроксимации: максимальные значения F-критерия, R, R-квадрата; минимальные значения МНК и относительной ошибки аппроксимации (Eotn); отсутствие автокорреляции в остатках на основе критерия Дарбина-Уотсона (Dkr) (табл. 3.3). Таблица 3.3 Формальные критерии аппроксимации модели

Форма связи	Eotn	F-крит	МНК	R	Dkr
Стеренная	8,738	8,346	0,87	0,758	2,191

Статистическая достоверность уравнения связи была проверена на основе F-критерия:

Поскольку то с вероятностью 0,85 можно утверждать, что степенное уравнение связи статистически достоверно.

Значимость коэффициента множественной корреляции была проверена на основе t-критерия:

Поскольку то с вероятностью 0,85 можно утверждать, что коэффициент множественной корреляции статистический значимый.

Статистическая достоверность параметров уравнения была проверена на основе t-критерия:

Поскольку , то с вероятностью 0,85 можно утверждать, что параметры а0, а1, а2 и а3 статистически недостоверны в связи с малым числом степеней свободы.

- определение прогнозных значений результативного показателя по выбранному уравнению регрессии и доверительный интервал прогноза;

На первом этапе был осуществлен отбор моделей прогнозирования для факторов К и L. Исходя из формальных критериев аппроксимации оптималь- ной моделью для прогнозирования валовых капитальных инвестиций(К) была выбрана модель ОЛИМП, а для прогнозирования численности занятых в предпринимательстве (L) - параболическая модель.

Таким образом, прогнозные значения факторов, а также доверительные интервалы прогнозов представлены в таблице 3.4.

Подставив полученные прогнозные значения в исходное уравнение регрессии, рассчитаем прогнозные значения за период 2013-2017 гг. (табл.

3.5).

Таблица 3.4 Прогнозные значения и доверительные интервалы прогнозов факторов модели

Года	К				L
	Прогноз	ДИ			Прогноз		ДИ
2013	207,815	174,4	241,4	7561,141		6186,5		8935,8
2014	172,244	138,5	205,9	7143,012		5760,5		8525,5
2015	162,735	128,7	196,5	6688,009		5297,7		8078,3
.2016	177,392	143.3	211,4	6196,134		4798,1		7594,2
2017	191,907	157,9	225,9	5667,384		4261,7		7073,1

Таблица 3.5 Прогнозные значения и доверительный интервал объема реализованной продукции (Y) за 2013-2017гг

Годы	У	ДИ		К	L	t
		НГ ВГ
2004	1405,096			101,28	9581,7	1
2005	1514,549			106,179	9429,9	2
2006	1898.295			142,487	9272,5	3
2007	2414,715			205,063	9154,3	4
2008	3014,742			245,981	8969,4	5
2009	3102.361			190,839	8501,3	6
2010	3462,136			129,914	8186	7
2011	4091,411			191.314	8022,1	8
2012	4307,146			229,325	7920,9	9
2013	4390,127	4233,98	4499,1	207,815	7561,141	10
2014	4194,488	4093,12	4358,24	172,244	7143,012	11
2015	4022,609	3890,01	4155,13	162,735	6688,009	12
2016	3928,233	3759,99	4025,11	177,392	6196,134	13
2017	3800,675	3622,11	3887,23	191,907	5667,384	14

Доверительный интервал прогноза был рассчитан с учетом 2х погрешностей, при заданном значении t-критерия истандартной ошибки модели .

Таким образом, в последующие 5 лет объем произведенной продукции на предприятия, занимающихся предпринимательской деятельности будет снижаться и к 2017 г. с вероятностью 95% достигнет значения 3800,675 млрд. грн. (см. рис. 3.1).

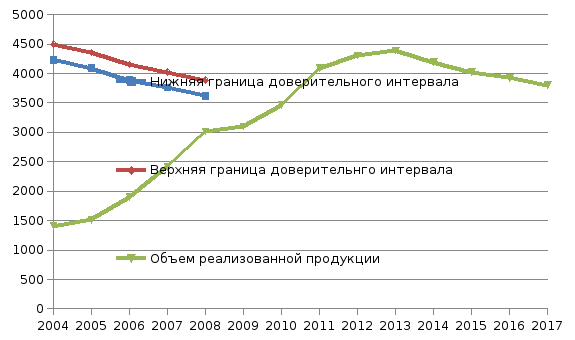
Рис 3.1. Прогнозные значения и доверительный интервал объема реализованной продукции на предприятиях, занимающихся предпринимательской деятельностью за 2013-2017 гг.