Блинков_ВЕ-31б_Отчет_Лаб-4 (ОТЦ)

Федеральное агентство связи ФГОБУ ВПО «Сибирский государственный университет

телекоммуникаций и информатики» Уральский технический институт связи и информатики (филиал)

Отчет к Лабораторной работе - 4, по дисциплине ТЭЦ

(Теория Электрических Цепей) - ОТЦ:

ИССЛЕДОВАНЕ ЧАСТОТНЫХ

ХАРАКТЕРИСТИК КОЛЕБАТЕЛЬ-

НЫХ КОНТУРОВ

Выполнил: Блинков. Е. М

Студент 2-го курса ВПО Группы ВЕ-31б.

Руководитель: Гуляев. В. П.

Екатеринбург

2015г.

1. Цель работы:

Экспериментальное исследование явления резонанса напряжений в электрических цепях. Измерение частотных характеристик последователь-

ного колебательного контура. Исследование влияния нагрузки на свойства последовательного контура. Применение последовательного колебатель-

ного контура в качестве режекторного фильтра.

2. Основные обозначения, расчетные формулы и определения:

Колебательными или резонансными цепями называются электриче-

ские цепи, в которых могут возникать явления резонанса напряжений или токов.

Резонанс – это такой режим электрической цепи, содержащей индук-

тивности и емкости, при котором ее реактивное сопротивление или реак-

тивная проводимость равны нулю. В последовательном колебательном контуре имеет место резонанс напряжений, то есть явление, при котором напряжения на реактивных элементах контура одинаковы и существенно превышают приложенное к цепи:

В этом выражении Q - добротность контура, определяемая как

Частота, на которой наблюдается резонанс напряжений, определяет-

ся выражением:

Входное сопротивление последовательного колебательного контура на резонансной частоте равняется R .

2

При подключении контура к источнику сигнала с сопротивлением RГ

и к нагрузке RН (рисунок 4.2) его добротность уменьшается:

Здесь RВН - вносимое в контур сопротивление.

Амплитудно-частотная и фазо-частотная характеристики колеба-

тельного контура описываются соотношениями:

где - обобщенная расстройка:

Полосой пропускания колебательного контура называется область час-

тот на границах которой его АЧХ уменьшается в 2 раз от максимального значения:

3

3. Расчетная часть:

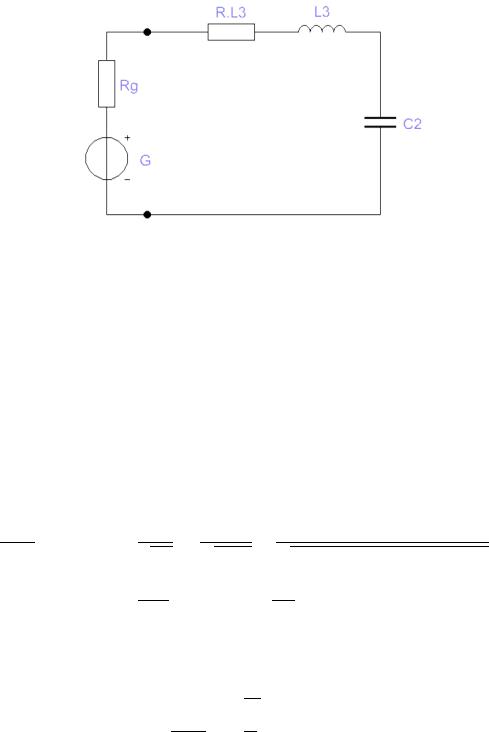
Для последовательного колебательного контура (Рис. 1.), составленного из элементов RL3, L3, C2, RГ = 50 [Ом] и действующим значением UД = = 2,2 [B]. Числовые данные к работе на 5 стенде: RL3 = 21 [Ом]; L3 = 41,3 [мГн]; C2 = 80,5 [нФ].

Рис. 1. Последовательный колебательный контур с подключенным ис-

точником сигнала.

Найдём:

1) Резонансная частота:

Так как контур последовательны мы будем наблюдать резонанс напря-

жений. Резонанс напряжений – это ситуация, когда напряжения на реактив-

ных элементах контура одинаковы и в добротность раз превышают входное.

2)Характеристическое сопротивление – величина, равная полному со-

противлению ёмкости или индуктивности на резонансной частоте:

4

3) Собственная добротность и затухание:

При резонансе напряжений реактивные составляющие скомпенсирова-

ны и сопротивление контура носит чисто активный характер. Добротность контура можно определить как:

Затухание:

Добротность при подключении нагрузки в виде резистора

R4 = 19 [кОм] (Рис. 2.):

Затухание при подключении нагрузки:

4)Комплексный ток и напряжение на элементах контура на резонанс-

ной частоте:

5)Полоса пропускания:

1). Ненагруженный контур.

5

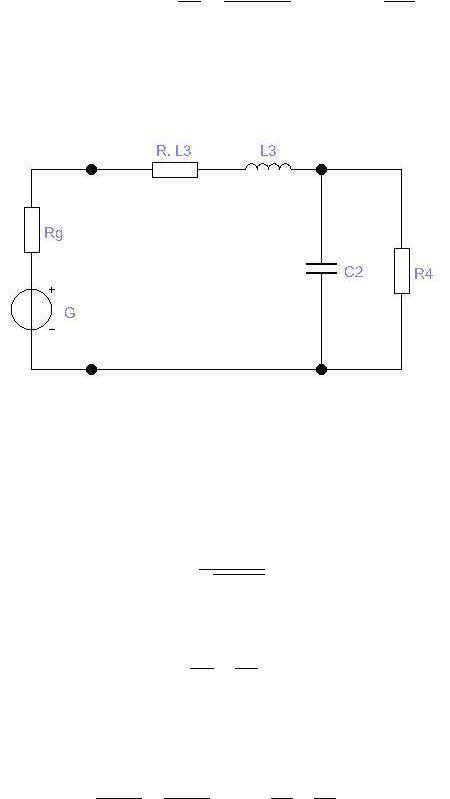
2). Нагруженный контур.

6) Сопротивление контура на резонансной частоте:

Рис. 2. Последовательный колебательный контур с подключенным источником сигнала и нагрузкой.

7) АЧХ контура в диапазоне частот, где её значения больше, чем на

20% от максимального. (Рис. 3.)

где - обобщенная расстройка:

Тогда можно записать:

6

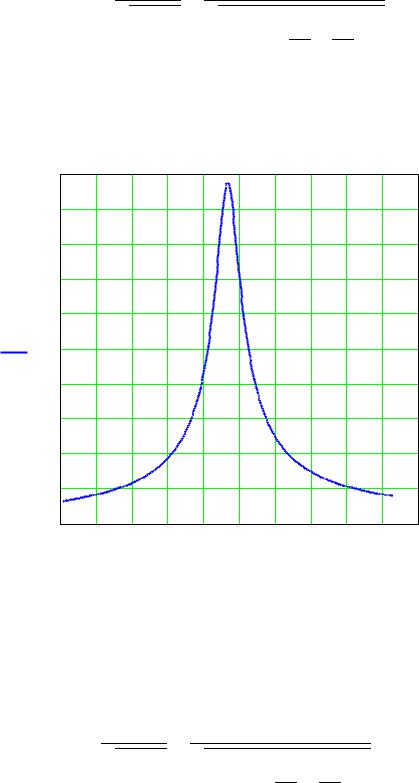
Где При добротности Q = 34,1

The p eak-frequency characteristic

Где

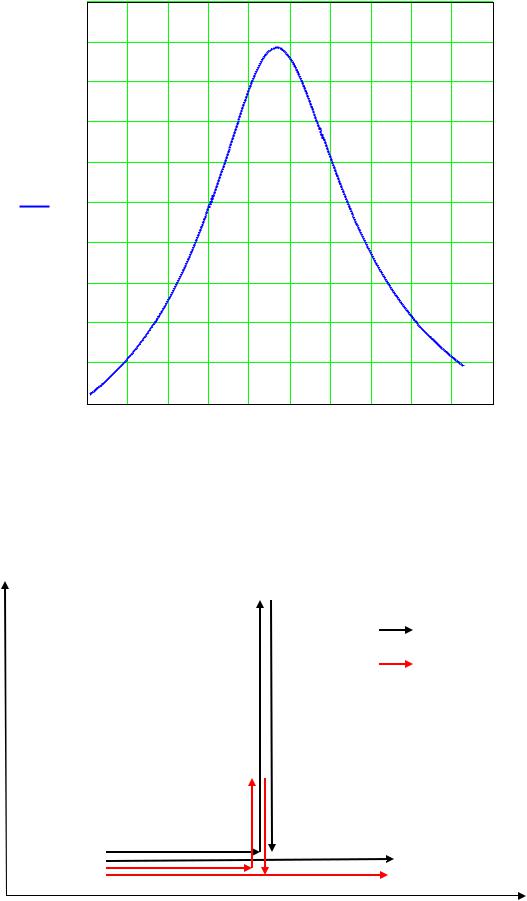
При добротности Q = 7,3 (Рис. 4.)

7

4.Экспериментальная часть:

4.1.Измерим величины сопротивлений R4 и RL3 катушки индуктив-

ности L3 сравним их значения с заданными при расчётах.

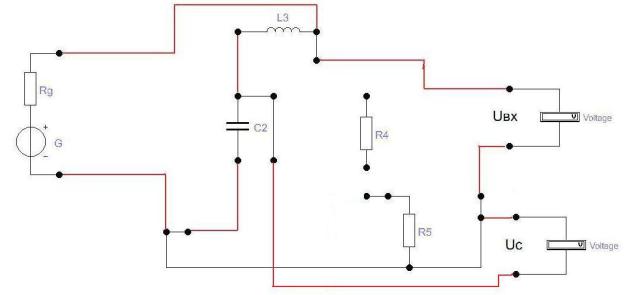
4.2. Соберём схему последовательного колебательного контура из элементов L3 и C2 блока «Простые и сложные цепи» лабораторного стенда. (Рис. 5.)

Рис. 5. Схема соединений на стенде для последовательного колебательного контура без нагрузки.

4.3.Установим на генераторе напряжение UГ = 2,2 [В] и частоту f0,

найденную при расчетах.

4.4. Снимем АЧХ контура, меняя частоту воздействия в диапазоне рассчитанных значений и измеряя напряжение не емкости С2.

Определим особые (ключевые) точки АЧХ (смотреть первую строку.

*UH – нормированное к входному напряжению, напряжение UC. (UH = UC / UВХ)

4.5.Снимем АЧХ контура при подключении к контуру нагрузки - со-

противления R4.

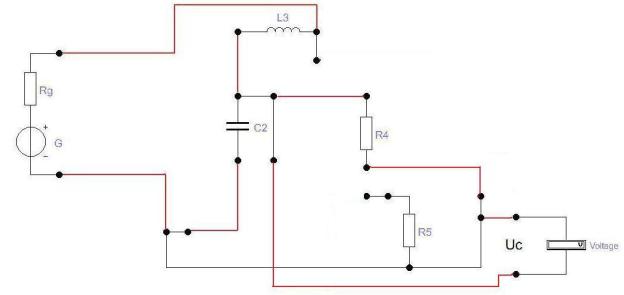
Не меняя напряжения воздействия, подключим к емкости нагрузочный резистор (Рис. 6.):

Рис. 6. Схема соединений на стенде для последовательного колебательного контура при подключении нагрузки.

*UH – нормированное к входному напряжению, напряжение UC. (UH = UC / UВХ)

10