2. Свойства комбинаторных объектов и чисел

1. =. Это свойство вытекает из формулы числа сочетаний.

2. =+.

3.

4. – бином Ньютона. В частности, (х + у)² = х² + 2ху + у²; (х + у)³ = х³ + 3х²у + 3ху² + у³ и т.д.

5. . Доказать легко с использованием бинома Ньютона на основе тождества (1 – 1)ⁿ = 0.

6. .

Контрольные вопросы и задания

1. Определить наибольший коэффициент разложения , если сумма всех его коэффициентов равна 4096.

2. Найти наибольший член разложения .

3. Найти коэффициент при в разложении

4. Определить число членов разложения .

5. Найти коэффициент при в разложении.

6. Найти коэффициент при в разложении.

7. Найти коэффициент при в разложении

.

8. Найти коэффициент при ив разложении.

9. В каком из выражений илибудет наибольший коэффициент при.

10. Доказать, что: .

11. Вычислить суммы:

    1. ;

    2. ;

    3. ;

    4. ;

    5. ;

    6. ;

    7. ;

    8. ;

    9. ;

    10. ;

    11. 

    12. .

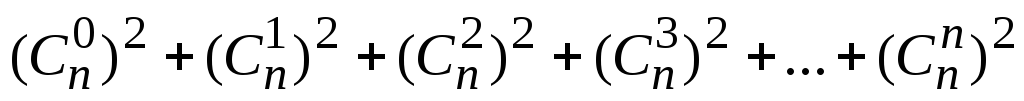
3. Методы изучения комбинаторных объектов и чисел

N₀ = N – + + … +

+ (– 1)^k + … + (–1)ⁿ N(1, 2, … , n). (1)

N_k = + …+(– 1)^s–k+

+…+ (–1)^n–k N(1, 2, … , n). (2)

Задача 1. В отделе НИИ каждый сотрудник владеет хотя бы одним иностранным языком. Известно, что английским языком владеют 6 человек, немецким – 6, французским – 7, английским и немецким – 4, немецким и французским – 3, английским и французским – 2, все три языка знает 1 человек. Определить, сколько всего человек в отделе, сколько человек владеют только английским, только немецким, только французским, и сколько человек знает только 1 иностранный язык.

Решение. Согласно условиям задачи N₀ = 0, т.к. в отделе нет сотрудников, не владеющих иностранными языками. Следовательно, по формуле (1) получаем:

N = – + N(1, 2, 3) (3)

N = (6 + 6 + 7) – (4 + 3 + 2) + 1 = 11 человек всего в отделе.

Для вычисления остальных показателей также воспользуемся формулой (1). Найдем, например N(только А) – число человек, не владеющих никаким другим языком, кроме английского. Для этого формулу (1) надо применить только к множеству людей, владеющих английским языком. В этом случае n = 2. Тогда N = N(A), N(1) и N(2) – число людей, владеющих, помимо английского, еще немецким и французским, соответственно, N(1, 2) – число людей, владеющих помимо английского еще одновременно немецким и французским. Отсюда

N(только A) = 6 – (4 + 2) + 1 = 1.

Аналогично

N(только Н) = 6 – (4 + 3) + 1= 0.

N(только Ф) = 7 – (2 + 3) + 1 = 3.

Вычислим теперь N₁ – число людей, владеющих только 1 языком. Воспользуемся формулой (2) при k = 1.

N₁ = N(1) + N(2) + N(3) + (–1)^2–1 [N(1,2) + N(2,3) + N(1,3)] +

+ (–1)^3–1 N(1,2,3) = 6 + 6 + 7 – 2(4 + 3 + 2) + 31 = 4.

Такой же результат получим, если сложим N(только A) + N(только Н) + N(только Ф).

Задача 2. Найти производящую функции, формулу общего члена последовательности и , зная рекуррентное соотношениеи начальные члены,.

Решение. Найдем производящую функцию последовательности

.

Коэффициенты определим как коэффициенты произведения производящих функций из соотношений:

, .

Следовательно, .

Формулу общего члена последовательности можно получить, разложив производящую функцию на простые дроби и приведя подобные при одинаковых степенях. Однако проще воспользоваться теоремой об общем виде решения линейного рекуррентного соотношения. Выпишем характеристический многочлен соотношения и найдём его корни.

Уравнение , согласно теореме Виета имеет два простых корня, т.е.. Тогда общее решение линейного рекуррентного соотношения имеет вид

.

Коэффициенты определяются из начальных условий, т.е. из системы линейных уравнений. Решив данную систему, получим. Следовательно,, а.