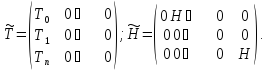III. Теоремы о кратной полноте системы собственных и присоединенных векторов операторного пучка.
1. Постановка вопроса о кратной полноте возникла у М.В. Келдыша в связи с рассмотрением для векторной-функций x(t) со значениями δ операторного дифференциального уравнения вида:
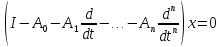 (3.1)
(3.1)
где
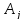 (j=1,2,…,
n)
– некоторые операторы из
(j=1,2,…,
n)
– некоторые операторы из
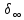 .
.
Как и для случая уравнений (3.1) в конечномерном пространстве, общая теория уравнений (3.1) основана на теории операторных пучков:
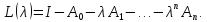
Если
искать решения уравнения (3.1) в виде:
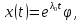 где вектор
где вектор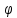
из δ не зависит от t, то мы естественно придем к уравнению
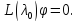
Число
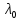 называетсяхарактеристическим
числом пучка
называетсяхарактеристическим
числом пучка
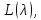 если
уравнение
если
уравнение
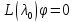 имеет нетривиальные решения
имеет нетривиальные решения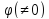 .
Последние называютсясобственными
векторами пучка
.
Последние называютсясобственными
векторами пучка
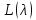 .
.
Если
некоторая функция
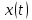 вида
вида
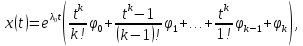 (3.2)
(3.2)
где
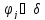 (j=1,2,…,
k;
(j=1,2,…,
k;
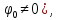 является решением уравнения (3.1), то
решениями этого уравнения будут также
функции
является решением уравнения (3.1), то
решениями этого уравнения будут также
функции
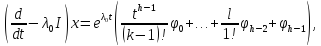 ……………………………………
……………………………………
Отсюда
следует, что
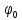 есть собственный вектор пучка
есть собственный вектор пучка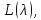 отвечающий числу
отвечающий числу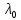 .
.
Легко видеть, что функция x(t) вида (3.2) будет решением уравнения (3.1) в том и только в том случае, когда выполняются соотношения:
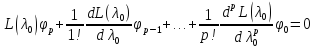 (3.3)
(3.3)
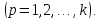
Векторы
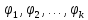 называютсяприсоединенными
векторами к
собственному вектору
называютсяприсоединенными
векторами к
собственному вектору
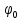 .
Числоk+1
называется длиной
цепочки
.
Числоk+1
называется длиной
цепочки
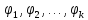 ;
оно может быть как конечным, так и
бесконечным. Вектор
;
оно может быть как конечным, так и
бесконечным. Вектор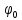 называется собственным вектором пучкаконечного
ранга
r, если наибольшая по длине цепочка,
отвечающая вектору
называется собственным вектором пучкаконечного
ранга
r, если наибольшая по длине цепочка,
отвечающая вектору
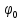 ,
имеет длину равнуюr.
,
имеет длину равнуюr.
Собственное
число
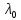 пучка
пучка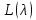 называется собственным числомконечной
алгебраической кратности, если
подпространство
называется собственным числомконечной
алгебраической кратности, если
подпространство
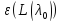 (нулей оператора
(нулей оператора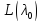 )
конечномерно и ранги всех собственных
векторов
)
конечномерно и ранги всех собственных
векторов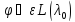 )
ограничены одним и тем же числом.
)
ограничены одним и тем же числом.
Очевидно,
что при переходе от пучка
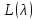 к пучку
к пучку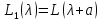 (a
– любое комплексное число) спектр
характеристических чисел
(a
– любое комплексное число) спектр
характеристических чисел
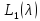 получается из спектра
получается из спектра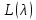 сдвигом
сдвигом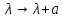 ,
а собственные и присоединенные векторы
сохраняются.
,
а собственные и присоединенные векторы
сохраняются.
Отметим, что метод доказательство приводимых ниже предложений состоит в сведении полиномиального операторного пучка к линейному пучку.
1.
Если
хотя бы в одной точке
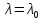 оператор
оператор
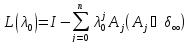
обратим,
то множество характеристических чисел
пучка
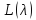 состоит из изолированных точек конечной
алгебраической кратности.
состоит из изолированных точек конечной
алгебраической кратности.
В
самом деле,
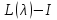 является целой оператор-функцией,
принимающей значения из
является целой оператор-функцией,
принимающей значения из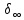 ,
и оператор
,
и оператор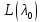 обратим, а следовательно, в силу теоремы
оператор
обратим, а следовательно, в силу теоремы
оператор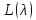 обратим всюду, за исключением, быть
может, некоторого множества изолированных
точек, являющихся характеристическими
числами пучка
обратим всюду, за исключением, быть
может, некоторого множества изолированных
точек, являющихся характеристическими
числами пучка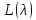 .
.
Для доказательство того, что каждое характеристическое число пучка имеет конечную алгебраическую кратность, перепишем уравнение (3.1) в виде уравнения первого порядка. С это целью образуем гильбертово пространство δ, равное ортогональной сумме n копий пространство δ. Тогда уравнение
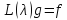
можно записать в виде системы
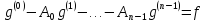
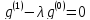
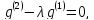
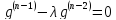
где
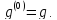 Таким образом, оно эквивалентно
следующему уравнению в пространстве
δ:
Таким образом, оно эквивалентно
следующему уравнению в пространстве
δ:
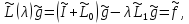 (3.5)
(3.5)
где
g=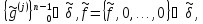 а операторы
а операторы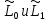 определяются в
определяются в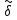 матрицами
матрицами


Из
эквивалентности уравнений (3.4) и (3.5)
непосредственно следует, что линейный
пучок
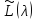 имеет те же характеристические числа,
что и пучок
имеет те же характеристические числа,
что и пучок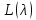 .
.
Кроме
того, нетрудно показать, что вектор
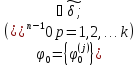 – присоединенными векторами к
– присоединенными векторами к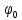 в том и только в том случае,
в том и только в том случае,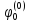 является собственным, а
является собственным, а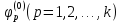 – присоединенными к нему векторами
пучка
– присоединенными к нему векторами
пучка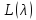 ,
отвечающими числу
,
отвечающими числу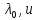
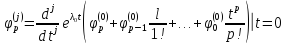
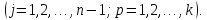
Отсюда
в частности, следует что длины
соответствующих цепочек присоединенных
векторов у пучков
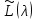 и
и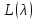 совпадают.
совпадают.
Без
ограничения общности можно предположить,
что оператор
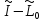 обратим (в противном случае мы бы перешли
от пучка
обратим (в противном случае мы бы перешли
от пучка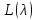 к пучку
к пучку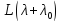 ).
Поэтому в силу отстояться показать, что
все ненулевые точки спектра оператора
).
Поэтому в силу отстояться показать, что
все ненулевые точки спектра оператора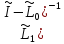 являются нормальными числами.
являются нормальными числами.
Нам уже известно, что все ненулевые точки спектра этого оператора являются изолированными точками.
Так как
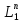 =
=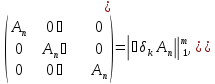
то
оператор
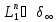 ,
а следовательно, весь его ненулевой
спектр состоит из нормальных собственных
чисел. Но тогда и ненулевой спектр
,
а следовательно, весь его ненулевой
спектр состоит из нормальных собственных
чисел. Но тогда и ненулевой спектр
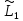 состоит из нормальных собственных
чисел.
состоит из нормальных собственных
чисел.
Так
как оператор
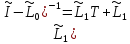 ,
где
,
где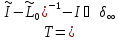 ,
то
точки
,
то
точки
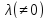 являются нормальными точками оператора
являются нормальными точками оператора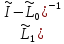 .
.
Предложение доказано.
2.
Сопоставим каждому характеристическому
числу
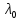 пучка
пучка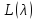 и каждой отвечающей ему системе
и каждой отвечающей ему системе из собственных векторов систему изnk
векторов
из собственных векторов систему изnk
векторов
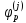 ,
построенных по правилу:
,
построенных по правилу:
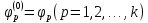
и
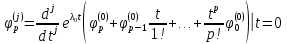
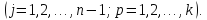
Следуя
М. В. Келдышу, назовем систему всех
собственных и присоединенных векторов
пучка
 n-кратно
полной,
если объединение всех систем вида
n-кратно
полной,
если объединение всех систем вида
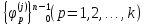 образует полную систему в пространстве
образует полную систему в пространстве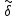 ,
равном ортогональной суммеn
копий пространство
,
равном ортогональной суммеn
копий пространство
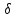 .
.
В случае n=1 это понятие сводится к понятию полноты в обычном смысле.
Вспоминая
доказательство предложения 1, приходим
к выводу, что система собственных и
присоединенных векторов пучка
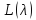 n-кратно
полна в том и только в том случае, когда
полна система собственных и присоединенных
векторов линейного пучка
n-кратно
полна в том и только в том случае, когда
полна система собственных и присоединенных
векторов линейного пучка
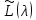 .
.
Отметим
еще, что для дифференциального уравнения
(3.1) n-кратная
полнота системы собственных и
присоединенных
векторов пучка
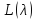 означает, что найдется решение x(t)
уравнения (3.1), являющееся линейной
комбинацией решение вида (3.2) с начальными
значениями x(0),
означает, что найдется решение x(t)
уравнения (3.1), являющееся линейной
комбинацией решение вида (3.2) с начальными
значениями x(0),
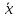 (0),….,
(0),….,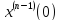 ,
сколь угодно близкими к любым наперед
заданным.
,
сколь угодно близкими к любым наперед
заданным.
Теорема
3.1.
Пусть
H-
произвольный полный нормальный оператор
конечного порядка и пусть при нескором
натуральном n
оператор
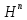 самосопряжен.
самосопряжен.
Тогда систем собственных и присоединенных векторов каждого из двух сопряженных пучков
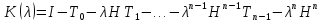 (3.6)
(3.6)
и
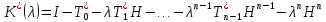 ,
(3.7)
,
(3.7)
где
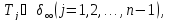 n-кратно
полна в
n-кратно
полна в
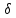 .
.
При
любом
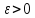 все характеристические числа пучка
все характеристические числа пучка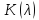 ,
за исключением, быть может, конечного
числа, лежит в углах
,
за исключением, быть может, конечного
числа, лежит в углах
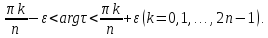
Доказательству этой теоремы предпошлем следующую лемму.
ЛЕММА
III.1
Пусть
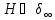 - произвольный нормальный полный
оператор,n-я
степень которого
- произвольный нормальный полный
оператор,n-я
степень которого
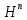 -
самосопряженный оператор, и пусть
-
самосопряженный оператор, и пусть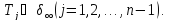
Тогда
для любого
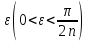 найдется
найдется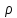 из
области
из
области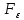 ,
получаемой из комплексной плоскости
удалением 2n
углов
,
получаемой из комплексной плоскости
удалением 2n
углов
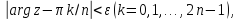 (3.8)
(3.8)
операторный пучок
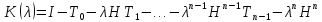
обратим и
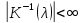 .
.
ДОКАЗАТЕЛЬСТВО.
Пучку
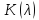 сопоставим линейный пучок
сопоставим линейный пучок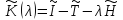 с оператором
с оператором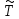 и
и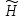 ,
определенными в ортогональном сумме
,
определенными в ортогональном сумме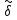 n
экземпляров
n
экземпляров
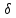 следующими матрицами:
следующими матрицами: