
II. Полиномиальный пучок и его линеаризация.
ЛЕММА II.1. Рассмотрим полиномиальный операторный пучок, т.е. операторный полином
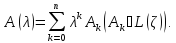 (2.1)
(2.1)
Степень
n
этого многочлена называется порядком
пучка (предполагаем, что
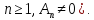 Пучок первого порядка называютлинейным,
а пучок второго порядка квадратичным.
Пучок первого порядка называютлинейным,
а пучок второго порядка квадратичным.
В спектральной теории пучков важную роль играют понятия спектра, регулярного значения, собственного значения, собственных и присоединенных векторов, производящего полинома, которые были введены в предыдущем параграфе для любой голморфной оператор-функции.
Одним
из основных методов в спектральной
теории пучков является метод линеаризации.
Он состоит в сведении различных задача
теории пучков к соответствующим задачам
для некоторого линейного
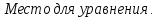 пучка
в пространстве
пучка
в пространстве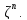 Этот метод аналогичен сведению
дифференциального уравненияn-го
порядка к системе n
уравнений первого порядка ( из дальнейшего
будет видно, что эта аналогия отражает
существенные связи между двумя теорями).
Этот метод аналогичен сведению
дифференциального уравненияn-го
порядка к системе n
уравнений первого порядка ( из дальнейшего
будет видно, что эта аналогия отражает
существенные связи между двумя теорями).
2. Здесь мы рассмотрим один из способов линеаризации пучка.
Обозначим через
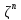 ортогональную суммуn
экземпляров пространства
ортогональную суммуn
экземпляров пространства
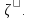 Иными словами,
Иными словами,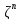 состоит из векторов-столбцов
состоит из векторов-столбцов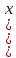 а
скалярного произведение в
а
скалярного произведение в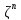 определяется равенством
определяется равенством
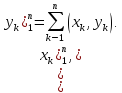 (2.2)
(2.2)
Операторы, действующие в
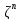 ,
удобно записывать в виде операторных
матрицn-го
порядка с элементами из L(
,
удобно записывать в виде операторных
матрицn-го
порядка с элементами из L(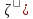 .
При этом, если
.
При этом, если
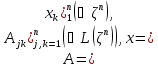 (2.3)
(2.3)
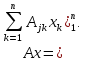 (2.4)
(2.4)
Диагональный оператор
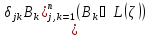 будем
обозначать через
будем
обозначать через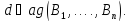
Поставим
в соответствие пучку (2.1) следующий
линейный пучок в пространстве
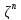 :
:
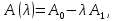
где
 (2.5)
(2.5)
(все не отмеченные элементы операторных матриц предполагаются равными нулю).
ЛЕММА
II.2.
Спектры пучком A(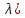 иA(
иA(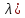 совпадают. Если оператор
совпадают. Если оператор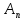 обратим, то спектр пучка А(
обратим, то спектр пучка А(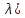 совпадает со спектром оператора
совпадает со спектром оператора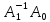 ,
и поэтому является непустым компактом.
Если оператор
,
и поэтому является непустым компактом.
Если оператор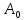 обратим, то спектр пучкаA(
обратим, то спектр пучкаA(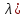 совпадает с множеством всех чисел вида
совпадает с множеством всех чисел вида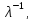 где
где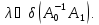
ДОКАЗАТЕЛЬСТВО.
Первое утверждение леммы вытекает из
леммы II.1. и обратимость
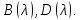 Если обратим оператор
Если обратим оператор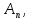 то
обратим и оператор
то
обратим и оператор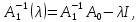 т.е. когда
т.е. когда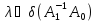 (мы сохраняем обозначениеI
для единичного оператора в пространстве
(мы сохраняем обозначениеI
для единичного оператора в пространстве
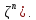 Аналогично, если обратим оператор с
Аналогично, если обратим оператор с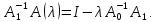 Отсюда вытекает последнее утверждение
леммы.
Отсюда вытекает последнее утверждение
леммы.
ЛЕММА
II.3.
Векторный
полином
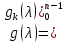 (с коэффициентами из
(с коэффициентами из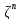 )
является производящим полином рангаm
пучка
)
является производящим полином рангаm
пучка
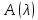 в точке
в точке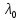 тогда и только тогда, когда
тогда и только тогда, когда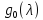 является производящим полиномом рангаm
пучка
является производящим полиномом рангаm
пучка
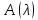 в точке
в точке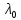 и
и
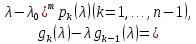 (2.6)
(2.6)
где
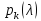 – векторные полиномы.
– векторные полиномы.
ДОКАЗАТЕЛЬСТВО.
Очевидно, что
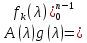 ,
где
,
где
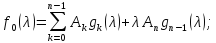 (2.7)
(2.7)
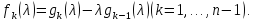 (2.8)
(2.8)
Если
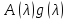 имеет в точке
имеет в точке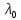 нуль кратности
нуль кратности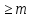 ,
то из (2.8) вытекает равенства (2.6), а из
них – равенства
,
то из (2.8) вытекает равенства (2.6), а из
них – равенства
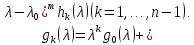 (2.9)
(2.9)
Кроме того, из (2.7) получаем, что
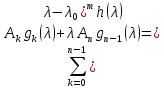 (2.10)
(2.10)
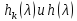 –некоторые
векторные полиномы). Подставляя (2.9) в
(2.10), получаем, что
–некоторые
векторные полиномы). Подставляя (2.9) в
(2.10), получаем, что
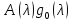 также имеет в точке
также имеет в точке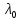 нуль кратности
нуль кратности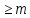 .
.
Обратно,
из (2.6) следует равенства (2.9), которые
вместе с равенства
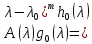 дают (2.10). Из (2.10) и (2.5) вытекает, что
дают (2.10). Из (2.10) и (2.5) вытекает, что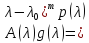 .
Лемма доказано.
.
Лемма доказано.
Легко
видеть, что в силу (2.6) полиномы
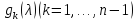
вместе
с
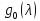 являются производящим полиномами для
пучка
являются производящим полиномами для
пучка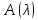 .
Нам понадобится связь между цепочками,
соответствующими полиномами.
.
Нам понадобится связь между цепочками,
соответствующими полиномами.
