20.Частотное регулирование скорости асинхронного двигателя с кз ротором

(изменение частоты питающей сети)

Возможность такого регулирования вытекает из выражения 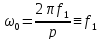1-статор

Частоту питающей сети регулируют с помощью тиристорных и транзисторных преобр. (ТПЧ).

Допустим,мы будем регулировать скорость, изменяя частоту при U1=const (на обмотке статора)

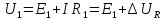
Пренебрежем ,Т.о.

Рассмотрим 2 случая регулирования скорости изменением частоты:

1)с целью увеличения скорости увеличиваем частоту

Уменьшение Ф при моменте статического сопротивления Мс=const приведет к перегреву двигателя.

Мс=Мд в установившемся рабочем режиме

2-на обмотке ротора

Увеличение I2 приводит к перегреву двигателя

2)с целью уменьшения скорости частоту ↓, значит Ф↑. А это приводит к насыщению магнитопровода, а значит к росту тока намагничивания.

Т.о.рассмотрев два варианта делаем вывод: регулирование скорости изменением частоты при U1=const не возможно, поэтому нужно искать закон изменения U1 при частотном регулировании скорости.

Такой закон попытаемся установить, взяв в качестве критерия работоспособности двигателя на любой частоте перегрузочную способность

Запишем критерий для двух различных частот

Параметры с индексом i разделим на параметры с индексом k

Параметр с индексом k будем считать номинальным. Если любой параметр разделить на его номинальное значение, то он будет выражен в относительных единицах.

–полный закон Костенко

1)q=0

Регулировочная характеристика

2)q=2

Вентиляторная характеристика

3)q=-2

Каждому механизму с его механической характеристикой соответствует свой закон управления, обеспечивающий работу двигателя на любой регулируемой характеристики в номинальном режиме.

Такой метод регулирования наиболее перспективный.

Максимальная скорость ограничивается механической прочностью ротора двигателя, а минимальная скорость ограничена возможностями получения синусоидального напряжения частотного преобразователя

1. Математическое описание элементов и систем управления

Математическим описанием являются уравнения статики (ур-ия установивш.режимов) и уравнения динамики (ур-ия переходных режимов). Физические величины, от которых зависят коэфф-ты ДУ, назыв-ся параметрами. Если параметры некот. элем. систем изм-ся во времени, то систему называют нестационарной или системой с переменными параметрами. В больш-ве случаев коэффициенты уравнения существенно не изменяются и системы являются системами с постоянными параметрами.

Удобной формой записи линейных дифференциальных уравнений является символическая или операторная. Переход к операторной форме осущ-ют введением сокращенного условного обозначения операции дифф-ия:

Для составления ур-ий, система разб-ся на отдельные звенья и для каждого из них записываются выражения относ-но входа и выхода. Совместное решение полученных уравнений дает мат.описание системы в целом.

Для лин. систем справедлив принцип суперпозиции, согласно которому уравнение выглядит:

Для получения анал-их решений, переходят от нелинейных ур-ий к приближенным линейным(линеаризация). В ее основе лежит предположение о том, что в процессе регулирования имеют место лишь малые отклонения от установившихся режимов. Линеаризация позв-ет перейти к уравнениям в приращениях и получить нулевые начальные условия. Для получения этих уравнений необходимо записать ур-ия статики, затем равновесие считать нарушенным и записать ур-ия динамики с учетом приращения всех переменных.

X0, Y0 – установ.знач.; дельты – приращения.

Из уравнений динамики вычитаются уравнения статики и получаются уравнения приращения

-ур-е динамики

-ур-е статики

-вычитаем.

В общем случае используется формула разложения в ряд Тейлора. При этом предполагают, что движение происходит в пределах малых отклонений, а все производные имеют единственное и конечное значение, отличное от 0.

Пренебрегают слагаемыми 2 и выше степеней отклонения переменных и вычитает уравнение статики получают уравнение в приращениях

Решение уравнений динамики:

Вид линеариз.уравнения сис-мы:

X_вых,X_вх,f – отклон-ия упр-ой перем-ой управл. и возмущающ.возд-ия от их установ-ся знач.

Решения УД :аналитические, графо-аналит-ие, численные.

Аналитические:

Свободная составляющая находится из решения ОДУ вида:. Уравнение вынужден.переменн.при скачкообразном вход. возд-ии хар-ет установив.режимы., опр-ся правой частью уравнения.

Временные характеристики:

1. Переходная характеристика h(t) – реакция звена или системы на един-ый ступенч. сигнал, который описывается:

График завис. Хвых(t) прямая параллельная оси х.

2. Импульсная перех.характер-ка – реакция звена(системы) на единич.импульсный сигнал:

Использование преоб-ий Фурье и Лапласа.

Любая ф-ция, удовл-ая усл-м Дирихле, являющ-ся периодич-ой с периодом Т, мб разложена в ряд Фурье.

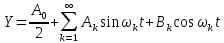
Непериод-ая ф-ция может рассм-ся как периодич. с периодом 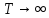. Используются 2 формулы:

-Прямого преобр-ия Фурье:

-Обратного преобр-ся Фурье:

Если в формулу прям.преобр. Фурье ввести показат.ф-цию , получится новая ф-ла прямого преобразования Лапласа:

-

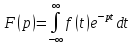
-Обратного преобразования Лапласа:

Получение операторного уравнения

Для получения операт.ур-ия по известному ДУ нужно знать начальные условия.

Если н.у. нулевые,то операторное уравнение мб получено из ДУ путем замены символа дифф-ия оператором Лапласа.

А,В,С -соответ-ие полиномы.

Передаточная функция:

Передаточная ф-ция – отношение изображений по Лапласу вых.и вх. переменных при н.н.у.

Передаточная ф-ция по управл.возд-ию:

Передаточная ф-ция по возмущ-му.возд-ию:

Передаточ.ф-ция не зависит от вида внешнего возд-ия, а зависит только от параметров элементов, составл-их систему. В передаточной ф-ции степень полинома числителя не должна превышать степень полинома знаменателя.

2. Частотные характеристики элементов и систем управления

Частотной функцией называется отношение изображений Фурье выходного и входного сигнала. Частотная функция по управляющему воздействию:

Частотная функция (ЧФ) может быть получена из передаточной с заменой P на j что эквивалентно преобразованию Лапласа к преобразованию Фурье. Графическое изображение частотной функции называется частотной характеристикой. Частотные характеристики описывают передаточные свойства элементов и систем в режиме установившихся гармонических колебаний, вызванных внешним гармоническим воздействием.

Если числитель и знаменатель ЧФ умножить на комплексно-сопряженное знаменателю уравнение, то выделяется веществ.и мнимая состав-ие:

По указанным составляющим мб построена амплитудно-фазовая частотная характеристика (АФЧХ). АФЧХ – г.м.т. концов вектора на комплексной плоскости при изменении частоты от - до .

ЧФ мб представлена в показательной форме:

–амплитудно – частотная характеристика (АЧХ)

- фазо – частотная характеристика (ФЧХ).

–вещественная частотная характеристика (ВЧХ)

- мнимая частотная характеристика (МЧХ).

Логарифмические частотные характеристики

Если ЧФ, представленную в показательной форме прологарифмировать, то

Отсюда видно, что при исследовании СУ пользуются 2 характеристиками:

1.Логарифмическая амплитудно-частотная характеристика (ЛАЧХ)

2.ЛФЧХ

При их построении исп-ся десятичные логарифмы. Для построения ЛАЧХ в оси ординат в равномерном масштабе откладывается(Дб)

В реальных системах в качестве упр-ых переменных используются напряжения и токи, которые находятся в квадратичной зависимости по отношению к мощности:

Изменению мощности в 10р соответствует изменение указан. величин в 100 раз, что соотв-ет 2 Белам или 20дБ.

По оси абсцисс откладывается частота в логарифмич.масштабе:

Для построения ЛФЧХ на оси ординат отклад-ся в равномерном масштабе величина фазы в градусах.

При построении ЛАЧХ исп-ся асимптотические хар-ки, сост-ие из отрезков прямых линий с опр-ым наклоном, кратному 20. Наклон асимптот выр-ся в дБ на декаду.

3. Общие условия устойчивости непрерывных САУ

Под устойчивостью понимается способность системы возвращаться в исходное или близкое к нему состояние после исчезновения внешних воздействий. Пусть система описывается след. линеаризованным ДУ:

Свободная составляющая, определяющая динамику системы, находится из однородного ДУ:

Система устойчива, если

Корни характеристического уравнения (к.х.у.) могут быть вещественными, комплексными, чисто мнимыми. Если веществ-ые корни отрицательны, то переходный процесс затухает монотонно; если положительны, то монотонно возрастает.

отрицательные корни

положительные корни

мнимые корни

Для устойчивости линейной САУ необходимо и достаточно, чтобы все кху имели отрицательные вещественные корни.

Для устойчивости линейной САУ необходимо и достаточно, чтобы все кху лежали слева от мнимой оси. Система будет находится на границе устойчивости при наличии нулевого или пары чисто мнимых корней. В случае нулевого корня в ХУ будет отсутствовать нулевой член

В этом случае устойчивость определяется относительно скорости изменения управляемой переменной. Значение управляемой переменной мб произвольным. Такая устойчивость – нейтральная.

Если в ХУ имеется пара чисто мнимых корней, то система находится на границе чисто колебательной устойчивости.

Необходимым, но недостаточным условием устойчивости является положительность коэффициентов ХУ.

Характеристическое уравнение это знаменатель передаточной функции, равный нулю. ХУ записывается в виде:

При перемножении сомножителей получим уравнение с полож-ми коэфф-ми.

Данное условие является необходимым и достаточным для устойчивости систем 1 и 2 порядка.

4. Общие условия устойчивости импульсных САУ

Решение разностного уравнения

Устойчивость определяется свободной составляющей которая находится:

Если подставить в однородное уравнение, то после преобразований получим ХУ:

Свободная составляющая будет стремиться к нулю, если все корни ХУ по модулю <1 (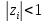) и число тактов

Процесс будет затухающим монотонным при положительных корнях и затухающим колебательным при отрицательных.

Если то система неустойчивая. Если хотя бы один из корней ХУ (+) и по модулю>1, то процесс будет монотонно расходящимся.

Если отрицательным, то:

Для устойчивости линейной импульсной САУ необходимо и достаточно, чтобы все корни ХУ были по модулю <1.

При дальнейшем изменении частоты вектор z будет описывать окружность. Границей устойчивости плоскости параметра z является окружность.

т.е. область устойчивости – внутр.часть круга с R=1. Для устойчивости линейных импульсных системы необходимо и достаточно чтобы все КХУ располагались внутри круга с R=1.

5. Алгебраические критерии устойчивости для непрерывных САУ

Критерии устойчивости делятся на алгебраические и частотные.

По алгебраическим КУ можно определить устойчивость с помощью коэффициентов ХУ.

Критерий Рауса. Для определения устойчивости необходимо составить таблицу Рауса по следующим правилам:

В 1-й строке записыв-ся коэффициенты ХУ с четными индексами, начиная с a₀, во второй – коэффициенты с нечетными индексами. Каждая послед-ая строка заполняется по алгоритму:

Общее число строк в таблице Рауса на порядок >ХУ.

Для устойчивости линейной САУ необходимо и достаточно, чтобы все коэффициенты таблицы Рауса 1 столбца были положительны. По этому критерию можно определить кол-во корней с положительной вещественной частью. Оно равно числу перемен знака в 1 столбце.

Критерий Гурвица. Для определения устойчивости необходимо составить определитель Гурвица:

1)По главной диагонали записывается в порядке возрастания индексы, начиная с . Определитель заполняется по столбцам. Вниз по главной диагонали записываются коэффициенты с убывающим индексом, вверх – с возрастающим. Недостающие заполняются нулями.

Формулировка: Для устойчивости линейной САУ необходимо и достаточно, чтобы определитель Гурвица и его диагональные миноры были положительными.

Если все определители низших порядков положительны, то система будет находиться на границе устойчивости, если старший определитель =0.

– система на границе апериодической устойчивости;

- на границе колебательной устойчивости.

С помощью этого критерия можно найти критическое значение любого параметра, при котором система находится на границе устойчивости. Считая искомый параметр неизвестным, составляется критерий Гурвица, затем, принимая решают его относительно искомого параметра.

6. Особенности использования алгебраических критериев устойчивости для импульсных САУ.

Использование алгебраических критериев по характ.урав-ию в z-изображении не представляется возможным, поэтому необходимо перейти к v – преобразованиям:

При переходе к v – преобразованию окружность R=1 вновь отображается в мнимую ось.

Характеристическое уравнение становится однозначной функцией и для определения устойчивости можно воспользоваться любым алгебраическим критерием.

Условие устойчивости по Гурвицу:

7. Частотные критерии устойчивости для непрерывных САУ

Критерии устойчивости делятся на алгебраические и частотные. В основе всех частотных критериев лежит принцип аргумента. Пусть характеристический полином имеет вид:

Каждый сомножитель характеристического полинома можно представить на комплексной плоскости в виде вектора, проведенного из точки в произвольную точкуP.

Вращение вектора против часовой стрелки положительное. Тогда при изменении частоты от - до + вектор, соответствующий левому корню повернется на угол π, а правому – на угол –π.

Критерий Михайлова.

Пусть хар-ий полином имеет вид:

При изменении частоты будет перемещаться в комплексной плоскости.

Условие необходимо, но недостаточно для устойчивости системы. В устойчивой системе не дб корней обращающих в ноль вектор .

Для устойчивости линейной САУ необходимо и достаточно, чтобы вектор при изменении частоты от 0 до повернулся от начала координат против часовой стрелки, нигде не обращаясь в ноль на угол .

При практических расчетах определяется ХУ, в котором P заменяется на и выделяется вещественная и мнимая составляющие. По ним при изменении частоты от 0 до на комплекс.плоскости строится годограф Михайлова, по его виду определяется устойчивость системы на основании след.формулировки: для уст-ти лин-ой САУ необх.и дост-но,чтобы годограф при изменении частоты от 0 до  начинаясь на вещ-ой (+) полуоси проходил послед-но против час.стрелки, нигде не обращаясь в ноль, n квадрантов.

Критерий Найквиста

позволяет определить устойчивость замкнутой системы по частотным характеристикам разомкнутой системы.

Пусть передаточная функция разомкнутой системы имеет вид:

Пусть ХУ разомкнутой системы имеет L правых и (n-l)левых корней. Согласно принципа аргумента, получим

Если замкнутая система будет устойчивой, то m=0,

Замкнутая система устой-ва, если частотная характеристика вспомогательной функции охватывает начало координат раз. Переходя от вспомогательной функции к частотной ф-ции разомкнут. системы, формулируется критерий Найквиста.

Если разомкнутая система неустойчивая, имеет L правых корней, то для устойчивости замкнутой САУ необходимо и достаточно, чтобы АФЧХ разомк. системы при изменении частоты от 0 до  (от 0 до) охватывала точку с координатами (-1;j0) в положительном направлении L/2 раз.

В логарифмических:

Для определения устойчивости необходимо построить ЛАЧХ и ЛФЧХ разомкнутой системы. Устойчивость замкн. САУ оценивается по взаимному положению этих характеристик с учетом того, что устойчива или неустойчива разомкнутая система.

Формулировка:Если разомкнутая система устойчива, то для устойчивости замкнутой САУ необходимо и достаточно, чтобы ЛФЧХ разомкн.системы пересекала линию -180 справа от частоты среза.

Если разомкнутая система неустойчивая, имеет L правых корней, то для устойчивости замкнутой САУ необходимо и достаточно чтобы разность м-у числом положительных и отрицательных переходов ЛФЧХ разомкн.системы через линию -180 в диапазоне частот, где L() >0, была равна L/2.

8. Особенности использования частотных критериев устойчивости для импульсных САУ.

Частотные критерии устойчивости позволяют определить устойчивость по виду соответствующей частотной характеристики.

Критерий Михайлова.

Пусть характеристический полином имеет вид:

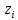–корни характеристического уравнения.

Угол поворота вектора от будет складываться из углов поворота элементарных сомножителей.

Если все корни внутри окружности , то суммарный угол поворота равен .

Если корень располагается вне единичной окружности, то угол поворота равен нулю, суммарный угол поворота будет меньше .

Для устойчивости линейной системы необходимо и достаточно чтобы вектор 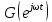при изменении частоты от повернулся против часовой стрелки вокруг начала координат на угол.

При практических расчетах находится ХУ:

Выделяются вещественная и мнимая составляющие:

При изменении частоты от 0 до на комплексной плоскости строится годограф Михайлова и по его виду определяется устойчивость в соответствии с формулировкой.

Для устойчивости импульсной САУ необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от 0 до начинаясь на вещественной положительной полуоси, проходил последовательно в положительном направлении, нигде не обращаясь в ноль, 2m квадрантов.

Критерий Найквиста.

Позволяет определить устойчивость замкнутой системы по частотной характеристике разомкнутой системы. Находится дискретная передаточная функция разомкнутой системы:

Рассмотрим вспомогательную функцию:

Здесь – характеристический полином замкнутой системы.

–характеристический полином разомкнутой системы.

Предположим что ХУ разомкнутой системы имеет l корней вне окружности единичного радиуса, тогда

Если замкнутая система будет устойчивой, то

С учетом этого, вспомогательная функция при изменении частоты

Переходя от вспомогательной функции к частотной функции разомкнутой системы, формул-ся критерий Найквиста:

Если разомкнутая система неустойчива, имеет l корней вне окружности R=1, то для устойчивости замкнутой САУ необходимо и достаточно чтобы ЧХ системы при изменении частоты от 0 до охватывала точку с координатами (-1;j0) раз в положительном направлении (1).

1.2.

Если разомкнутая система устойчива, то для устойчивости замкнутой САУ необходимо и достаточно, чтобы ЧХ разомкнутой системы при изменении частоты от 0 до не охватывала точку с координатами (-1;j0) (2).

9. Синтез параллельных корректирующих устройств

Синтезом называется выбор параметров и структуры так, чтобы она удовлетворяла заданным показателям качества регулирования. Если система неустойчива или не удовлетворяет заданным показателям, то производится коррекция. Различают непрерывные, дискретные корректирующие устройства.

Непрерывные корректирующие устройства делятся на последовательные и параллельные.

Параллельная коррекция включается либо параллельно ИЭ или НЧ, либо в виде местных обратных связей.

Изменяя параметры КУ можно так деформировать ЛАЧХ системы, что она станет устойчивой и будет удовлетворять заданным показателям качества регулирования.

Линейные системы:

Паралл.коррекция включается в виде местных обратных связей, как правило отрицательных. Охватывает звенья с наибольшим коэффициентом усиления или постоянной времени. При охвате более 2 звеньев нужно проверить на устойчивость внутренн.контур. КУ включаются как можно ближе ко входу системы.

Передаточная функция контура с местной ОС

переписать с заменой .

Для наиболее существенной области частот справедливо неравенство:(1) Тогда

Структурная схема выражается:

Динамические свойства контура с местной ОС определяются только характеристикой КУ. Передаточная ф-ция разомкнутой системы с паралл.корр.имеет вид:

переписать с заменой.

При выполнении условия (1) можно пренебречь единицей и частотная функция будет иметь вид:

10. Синтез последовательных корректирующих устройств.

Синтезом называется выбор параметров и структуры так, чтобы она удовлетворяла заданным показателям качества регулирования. Если система неустойчива или не удовлетворяет заданным показателям, то производится коррекция. Различают непрерывные, дискретные корректирующие устройства.

Непрерывные корректирующие устройства делятся на последовательные и параллельные. Последовательная коррекция включается либо на входе импульсного элемента, либо на входе непрерывной части системы.

Последовательная коррекция изменяет частотные свойства непрерывной части системы. Тот же эффект м.б. достигнут изменением формы импульса. В этом случае, в систему включается дополнительный формир.элемент, рассматриваемый как последовательное КУ.

При синтезе дискретная система заменяется непрерывной, динамика которой близка к импульсной, что справедлив в том случае, если частота коммутации является большой и в системе имеются инерционные элементы.

Расчетная структурная схема импульсной системы имеет вид:

При достаточно малых значениях Т можно перейти:

1

Wк(p)

Wну(p)

Синтез проводится методами линейных непрерывных систем, например метод ЛЧХ.

Линейные системы:

Последовательная коррекция включается последовательно в основной контур регулирования. Его включают либо после звена сравнения, либо после предварительного усилителя. Структурная схема имеет вид:

Передаточная функция разомкнутой системы:

11. Метод фазовой плоскости

Метод фазовой плоскости относится к точным методам исследования нелинейных САУ. Состояние системы в любой момент времени t определяется управляемой переменной и ее (n-1) производной. Если эти величины отложить на осях координат, то полученное n – мерное пространство называется фазовым пространством. Состояние системы в каждый момент t определяется точкой, котор. Называется изображающей. Во время переходного процесса изобр-ая точка перемещается в фаз.простр-ве по фазовой траектории.

В установившемся режиме точка находится в состоянии покоя и называется особой точкой. Совокупность фазовых траекторий для различных начальных условий совместно с особыми точками называется фазовым портретом системы.

При исследовании системы данным методом структурная схема преобразуется к виду:

Где ЛЧ это линейная часть системы, НЭ нелинейный элемент.

С помощью перейдем от уравнения 2 порядка к 2 уравнениям 1го порядка

Разделив 2 уравнение на 1, получим

Если удастся найти аналитическое выражение y=f(x), то можно построить для разных н.у. семейство фазовых траекторий, т.е. получить фазовый портрет.

Свойства фазовых траекторий:

1. Изображающая точка в верхней полуплоскости движется слева направо,а в нижней справа налево. (по часовой стрелке)

2. Фазовая траектория пересекает ось абсцисс под 90 град.

3. Фаз.траектории не пересекаются между собой, за исключением особых точек.

Типы особых точек: узел, фокус ,центр, седло.

Изоклиной называется ГМТ фаз.плоскости, которые фаз.траектория пересекает под одним и тем же углом. При использовании метода изоклин нелинейная характеристика разбивается на линейные участки и для каждого из них записывается лин. ДУ. Правая часть уравнения приравнивается к константе и решается относительно переменной У, в результате будет получено уравнение изоклины. Построение ведется так,чтобы фаз.плоскость была заполнена равномерно изоклинами.

На каждой изоклине изображается вспомогательная кривая под углом α к ох

Полученные точки соединяются плавной кривой, в результате строится фазовая траектория