12.Метод гармонической линеаризации

В основе метода гармонической линеаризации лежит принцип гармонического баланса, основанный на гипотезе фильтра и предположении о гармоническом характере свободного движения системы. При использовании данного метода структурная схема должна быть преобразована к виду:

Рассмотрим прохождение гармонического сигнала через разомкнутую гармоническую систему.

Сигнал периодический, поэтому м.б. разложен в ряд Фурье:

Если нелинейность симметричная, то А₀ = 0. На лин-ую систему подается сигнал, содержащий весь спектр частот, каждая гармоника сигнала действует независимо от других. На выходе лин.части появятся колебания, содержащие те же частоты, как на входе, амплитуды будут различны. Для исследования степени изменения амплитуды строится АЧХ линейной части системы. Если амплитуда основной гармоники несоизмеримо больше амплитуд гармоник, то лин.часть явл-ся фильтром и гасит все высшие гармоники.

Гармоническая линеаризация заключается в том, что записывается ряд Фурье для выходной характеристики для НЭ, в котором учитывается только 1 гармоника. В результате получается аналитическая линейная зависимость, между входом и выходом нелинейного звена. Для однозначной симметричной нелинейности записывается:

Для неоднозначной симметричной нелинейности:

Для замкнутой системы:

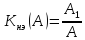–коэффициент гармонической линеаризации нелинейного звена.

Для неоднозначной:

- коэффициент гармонич. линеаризации, учитывающий производную от нелинейной функции

13.Критерий устойчивости Найквиста на комплексной плоскости

Критерий Найквиста позволяет определить устойчивость замкнутой системы по частотным характеристикам разомкнутой системы.

Пусть передаточная функция разомкнутой системы имеет вид:

Пусть ХУ разомкнутой системы имеет L правых и (n-l)левых корней (для ИС l корней вне окружности R=1). Согласно принципа аргумента, получим

Замкнутая система устой-ва, если частотная характеристика вспомогательной функции охватывает начало координат 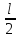раз. Переходя от вспомогательной функции к частотной ф-ции разомкнут. системы, формулируется критерий Найквиста.

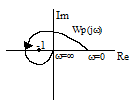
Если разомкнутая система неустойчивая, имеет L правых корней (l корней вне окружности R=1), то для устойчивости замкнутой САУ необходимо и достаточно, чтобы АФЧХ разомк. системы при изменении частоты от 0 до  (от 0 до) охватывала точку с координатами (-1;j0) в положительном направлении L/2 раз.

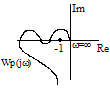
Правила перехода:

1. Переход частотной характеристикой разомкнутой системы ч-з вещественную ось слева от точки (-1;j0) считается полож-ым, если он происходит сверху вниз. Если разомкнутая система неустойчива и имеет l равных корней, то для устойчивости замкнутой САУ необходимо и достаточно, чтобы разность м-у числом + и – переходов частот. характеристикой разомкнутой системы ч-з вещественную ось слева от точки (-1;j0).

2. Если разомкнутая система устойчивая, то для устойчивости замкнутой САУ необходимо и достаточно, чтобы АФЧХ от 0 до  (от 0 до) не охватывала точку (-1;j0).