2.2. Связь автоматов с машинами Тьюринга

По сути, граф-схема машины Тьюринга представляет собой диаграмму переходов автомата, каждая метка которого состоит из двух слов, разделенных знаком →. Первое слово- то, что было на ленте, второе – то, на что заменяет его УУ в текущем такте, вместе с командным символом внутреннего алфавита.

ПримерПостроить машину Тьюринга, реализующую предикат “- четное число” (задано в унарной системе счисления) (см. задачу 51 из прошлого семестра).

Решение: Принцип работы соответствующей машины Тьюринга следующий:

УУ достигает конца числа в состоянииq₂, если число единиц четно, и в состоянииq₃, если число единиц нечетно, после чего она перемещается в исходное положение в состоянииq₄илиq₅и печатает И либо Л соответственно.

	0	1
q1	q0И	q3R
q2	q4L	q3R
q3	q5L	q2R
q4	q0И	q40L
q5	q0Л	q50L

В данном случае после выполнения программы среди пустых ячеек останется И либо Л. Если же надо сохранить на ленте исходное число , то в двух последних клетках таблицы надо заменитьq₄0Lнаq₄Lиq₅0Lнаq₅L(в петляхq₄иq₅граф-схемы алгоритма не стирать, а сохранять единицы).

2.3. Автоматы и автоматные языки

Лемма 2.3.1. Каждый автоматный язык распознаётся некоторым конечным автоматом, не содержащим переходов с метками длины больше единицы и имеющим ровно одно начальное состояние и ровно одно заключительное состояние.

Пример 2.3.2. Рассмотрим язык, заданный конечным автоматом (A, Q, , I, F), где A={a, b, c, d}, Q=F=I={1, 2}, ={<1,аb,2>, <2,cd,1>}.

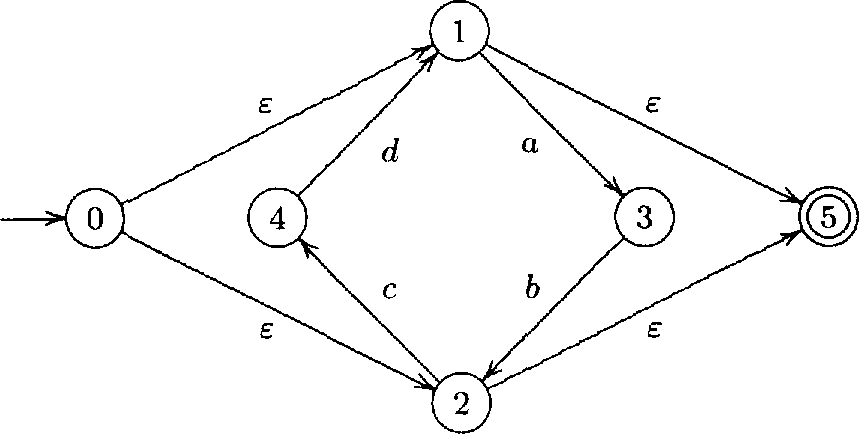
Тот же язык распознаётся конечным автоматом (A, Q’, ’, I’, F’), где Q’={0, 1, 2, 3, 4, 5}, I’={0}, F’={5}, ’={<1,a,3>, <3,b,2>, <2,c,4>, <4,d,1>, <0,,1>, <0,,2>, <1,,5>, <2,,5>}.

Здесь первые два перехода заменяют старый переход <1,аb,2> и следующие два перехода заменяют старый переход <2,cd,1>. Чтобы обеспечить единственность начального состояния, добавлены переходы <0,,1> и <0,,2>. Последние два перехода в ' обеспечивают единственность заключительного состояния.

Лемма 2.3.3 (об устранении пустых переходов). Каждый автоматный язык распознаётся некоторым конечным автоматом, содержащим только переходы с метками длины 1 и имеющим ровно одно начальное состояние.

Доказательство. Согласно лемме 2.3.1 можно предположить, что исходный язык задан конечным автоматом (A, Q, , I, F), не содержащим переходов с метками длины больше единицы, причём . Построим искомый конечный автомат (A, Q’, ’, I’, F’), положив Q' = Q, I’=I,

' ={<p, a, r> | aA и  такое qQ, что <q, a, r> и существует путь из р в q с меткой },

F' = {рQ | найдётся такое qF, что существует путь из р в q с меткой }. 

П

ример 2.3.4.Пусть _R=(A, Q, , I, F), где A={a, b}, Q={1, 2, 3}, I={1}, F={3}, ={<1,а,2>, <2,b,2>, <2,,3>, <3,а,3>}.

Л

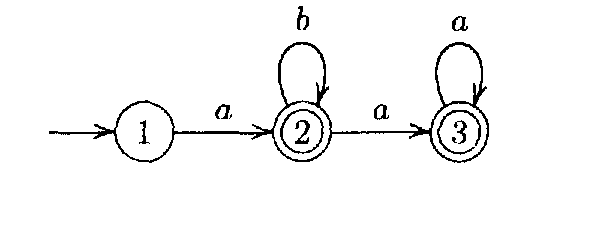
егко убедиться, чтоL(_R)=. Тот же язык распознаётся конечным автоматом (A, Q, ’, I, F’), где F’={2, 3} и ’={<1,a,2>, <2,b,2>, <2,a,3>, <3,a,3>}.

Теорема 2.4.1 (критерий автоматности формального языка). Язык является автоматным тогда и только тогда, когда он праволинейный.

Доказательство. Необходимость (каждый автоматный язык является праволинейным). По леммам 2.3.1 и 2.3.3 без ограничения общности можнопредположить, что исходный язык задан конечным автоматом _R=(A, Q, , I, F), где и. Положим N=Q, S=q₀ и .

Достаточность (каждый праволинейный язык является автоматным). Без ограничения общности можно предположить, что исходный язык задан праволинейной грамматикой, не содержащей правил вида Dи, где . ПоложимQ=N, I={S}, и , где. 