
Лк_4_ТелетрафикNGN 2013-03-26
.pdfКурс «Телетрафик сетей последующих поколений»
Вторая модель Эрланга
Лекция 4
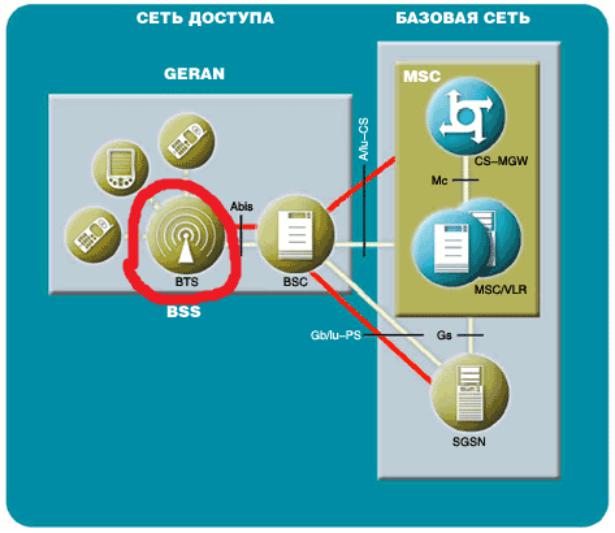
Модель 5. Модель с очередью
«Мультисервисный Эрланг» (с очередью)
Примеры моделей для анализа
сетей01.04пост.2013-NGN |
Примеры моделей для анализа сетей пост-NGN |
2 |
© Гайдамака Ю.В.
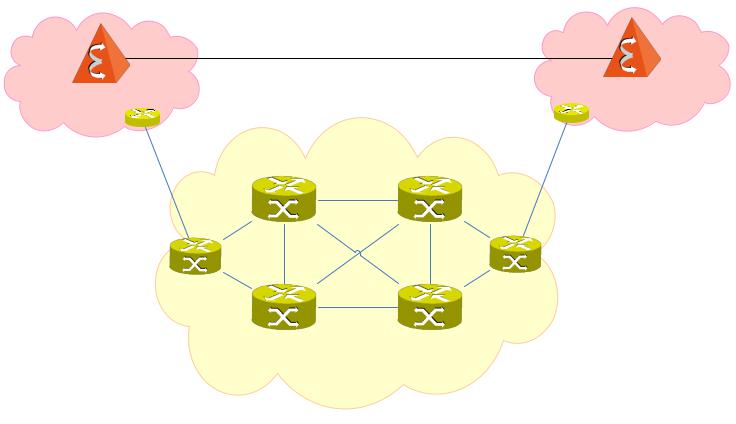
Фрагмент сети NGN
SIP
MGC |
MGC |
|
LSR |
LSR |
LER |
LER |
LSR |
Ядро IP/ LSR |
|
MPLS |
MGC - Media Gateway Controller
LER - Label Edge Router
LSR - Label Switch Router
01.04.2013 |
Примеры моделей для анализа качества в NGN |
3 |
© Гайдамака Ю.В.
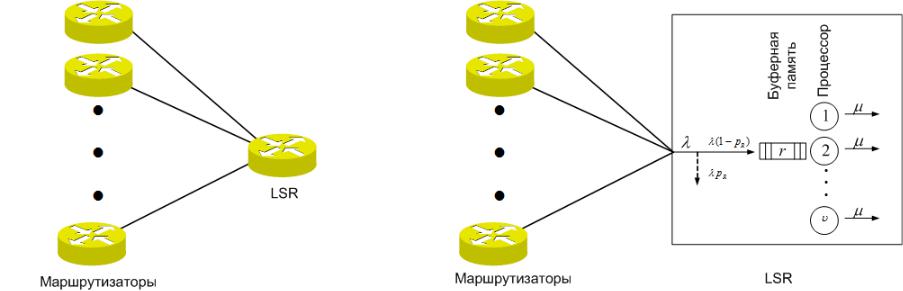
Модель узла LSR (1/2)
01.04.2013 |
Примеры моделей для анализа качества в NGN |
4 |
© Гайдамака Ю.В.
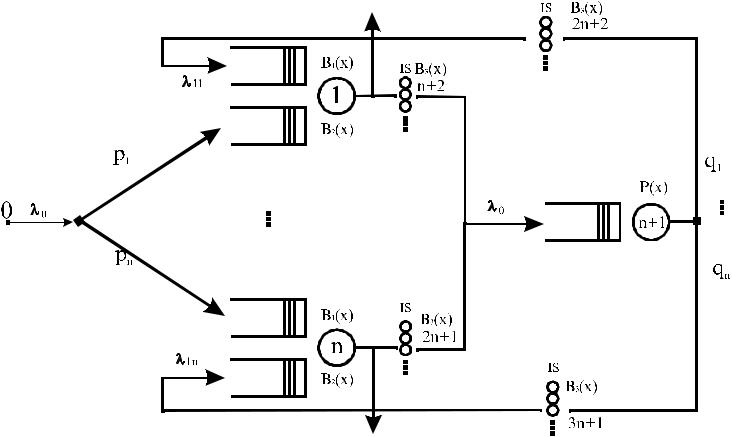
Модель узла LSR (2/2)
01.04.2013 |
Примеры моделей для анализа качества в NGN |
5 |
© Гайдамака Ю.В.
Схема 2-й модели Эрланга
|
M M |
|
|
|
|
Структурные параметры: |
|
|
|
|
r |
|
|
- количество приборов (линий |
|||
|
|
|
|
|
||||
|
|
|
|
|
пучка) |
|
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
r - количество мест в очереди |
|
|
|
|
|
|
|
|
R - емкость системы |
|
|
|
|
|
|
1 |
|
Нагрузочные параметры: |
|
|
|
|
|
|
|
- интенсивность входящего ПП |
||
|
|
|
|
|
|
|
||
|
1 |
|
|
r |
2 |
|
заявок |
|
|
|
|
|
|
- интенсивность |
|
||
|
|
|
|
|
|
|
экспоненциального распределения |
|
|
|
|
|
... |
|
СВ длительности обслуживания |
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
заявки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– вероятность блокировки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
заявки, pR |
|
01.04.2013 |
|
|
|
|
2-я модель Эрланга |
6 |
||
© Гайдамака Ю.В.
Физическая модель
•обслуживание хэндоверов в соте ССПС
•центральный процессор узла коммутации
•канал передачи данных
01.04.2013 |
2-я модель Эрланга |
7 |
© Гайдамака Ю.В.

Математическая модель
X (t) - число заявок в СМО в момент t, t 0
J 0,1, , R - пространство состояний системы,
Случайный процесс (СП) X (t) – ПРГ, X (t) J
pn lim P{X (t) n} - стационарная вероятность
t
состояния n J
pn , n J - стационарное распределение вероятностей ПРГ X (t)
01.04.2013 |
2-я модель Эрланга |
8 |
© Гайдамака Ю.В.

Диаграмма интенсивностей переходов
|
|
|
|
|
|
|
|
0 |
1 |
|
|
n |
|
|
v+r |
|
|
2 |
n |
(n+1) |
|
|
|
Интенсивности |
an,n 1 |
: n u(r n), |
переходов ПРГ X (t): |
an,n 1 |
: n min(n, ), |
|
an,n n n . |
|
01.04.2013 |
2-я модель Эрланга |
9 |
© Гайдамака Ю.В.

СУГБ
p0 p1 0;
pn 1 ( n ) pn (n 1) pn 1 0, n 1, 1;
pn 1 ( ) pn v pn 1 0, n , r 1;
p r1 p r 0.
01.04.2013 2-я модель Эрланга 10
© Гайдамака Ю.В.
