
Лк_5_ТелетрафикNGN 2013-04-09
.pdfСлучай dk 1, |
k K (3/3) |
Упр. 5.4. Убедиться, что при dk 1, k K , соотношения
(5.24) и (5.27) сводятся к (5.20) и (5.23)
соответственно.
09.04.2013 RLA: модель Келли 31
© Гайдамака Ю.В.

Модель Росса (1/3)
Система событий: |
|
Bk (l) {n N : dini Cl dk }, k K , l Lk |
(5.28) |
i K l
- на l -звене недостаточно свободной ШПП для установления соединения k -
класса, |
Bk (l) P(Bk (l)). |
|
|
Bk |
Bk (l), k K . |
|
|
l Lk |
|
|
|
Bk* 1 1 Bk (l) , |
k K |
(5.29) |
|
|
l Lk |
|
|
- условная вероятность блокировки запроса на установление многоканального соединения k-класса при условии, что блокировки на звеньях происходят независимо.
Bk (l) вычисляется с помощью модели отдельного звена по алгоритму Кауфмана-Робертса (5.13)-(5.15).
09.04.2013 |
RLA: модель Росса, |
32 |
|
многоканальные соединения |
© Гайдамака Ю.В. |
Модель Росса (2/3)
Вероятность блокировки установления соединения k-класса:
C
hl (n)l
B l |
n Cl dk 1 |
, k K l , |
|
|
|
(5.17) |
|||
|
|
|
|
|
|||||
k |
|
|
|
Cl |
|
|
|
|
|
|
|
|
|
hl (n) |
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0, |
|
n 0; |
|
|||||
h n |
1, |
|
|
n 0; |
(5.15) |
||||
l |
|
|
|
|
|
|
|
||
|
1 |
dk ak l hl n dk , |
|
|
|
|
|||
|
n 1,Cl , |
|
|||||||
|
|
|
|
||||||
|
|
|
|||||||
|
n k K l |
|
|
|
|
|
|||
ak (l) ak |
1 Bk ( j) , k K l , |
l L . |
(5.30) |
||||||
|
|
|
j Lk \{l} |
|
|
|
|
|
|
09.04.2013 RLA: модель Росса,
многоканальные соединения
33
© Гайдамака Ю.В.
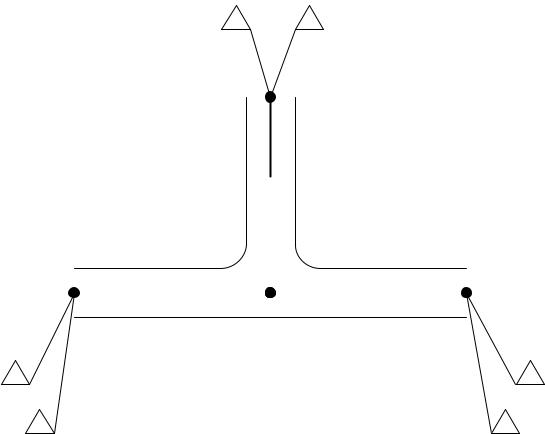
Модель Росса (3/3)
Упр. 5.5. Дано:
a1 1; a2 2, a3 1.
Выписать:
|
|
|
|
|
|
|
|
|
|
|
|
множества N , B , B , B |
; |
|
|||
|
|
|
|
|
|
|
1 |
2 |
|
3 |
|
|
|||||
|
|
|
|
|
=3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
просеянные нагрузки |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
ak l , k K , l L ; |
|
|
|
||
|
d1=2 |
|
|
|
|
|
|
|
|
d2=1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1=2 |
|
|
|
|
C3=2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
функции hl n , n 0,Cl , |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
d3=1 |
|
|
|
|
|
|
|
|
||||||||
l L ;
вероятности Bk (l), k K , l L .
09.04.2013 |
RLA: модель Росса, |
34 |
|
многоканальные соединения |
© Гайдамака Ю.В. |

Пример: постановка задачи
|
C2 |
a(l) |
|
C1 |
C3 |
09.04.2013 |
Модель отдельного звена |
35 |
© Гайдамака Ю.В.
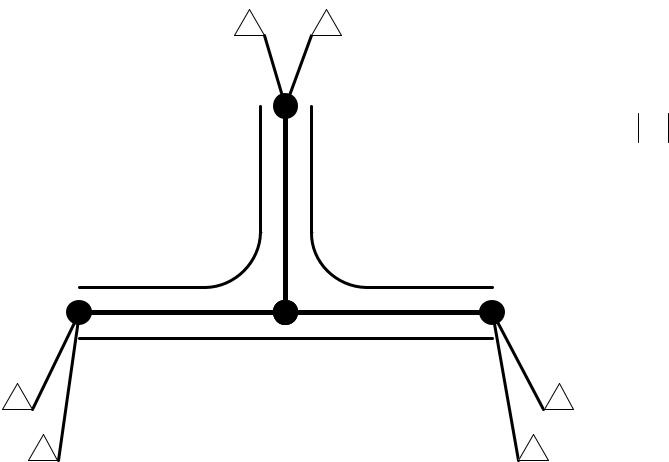
Пример: исходные данные
C1 2,C2 3,C3 2, C
 3
3
K {1, 2,3}, K 3
|
|
L1 {(1, 2)}, L2 |
{(3, 2)}, L3 {(3,1)} |
|
|
||||
C2 |
3 |
a 1, a 2, a 1; d 2, d |
2 |
1, d |
3 |
1 |
|||
|
|
1 |
2 |
3 |
1 |
|
|
||
d1 2 |
d2 1 |
|
|
|
|
|
|
|
|
C1 2 |
d3 1 |
C3 2 |
09.04.2013 |
Модель отдельного звена |
36 |
© Гайдамака Ю.В.

Пример: алгоритм получения решения
На первом шаге полагаем блокировки равными нулю, а нагрузку равной предложенной
По алгоритму |
С помощью |
Кауфмана-Робертса |
полученных |
считаем блокировки |
блокировок считаем |
с заданными |
просеянную |
нагрузками |
нагрузку |
Пользуясь критерием остановки работы алгоритма, получаем значение блокировок
09.04.2013 |
Модель отдельного звена |
37 |
© Гайдамака Ю.В.
Пример: критерий остановки алгоритма
LoadSum
prevLoadSum
LoadSum prevLoadSum
09.04.2013 |
Модель отдельного звена |
38 |
© Гайдамака Ю.В.
Пример: результаты
B1 1 1 B1 (1) 1 B1 (2) 0.387
B2 1 1 B2 (2) 1 B2 (3) 0.604
B3 1 1 B3 (1) 1 B3 (3) 0.656
0.001 |
iteration 8 |
0.0000001 |
iteration 13 |
09.04.2013 |
Модель отдельного звена |
39 |
© Гайдамака Ю.В.
