
Лк_5_ТелетрафикNGN 2013-04-09
.pdfПостановка задачи
Вероятность блокировки запроса на установление соединения k-класса:
Bk (n), k K . |
(5.9) |
||||||
|
|
|
|
n Bk |
|
||
Среднее число занятых единиц ёмкости на l* -звене: |
|
||||||
|
|
d (n) (n) . |
|
||||
d |
(5.10) |
||||||
|
|
n N |
|
||||
Коэффициент использования l* -звена: |
|
||||||
|
|
|
|
|
|
||
U |
d |
. |
(5.11) |
||||
|
|||||||
|
|
|
C |
|
|||
09.04.2013 |
Модель отдельного звена |
21 |
© Гайдамака Ю.В.

Модель стохастического ранца (1/3)
Для нахождения Bk применима модель стохастического ранца и алгоритм Кауфмана-Робертса.
C (n) n N : d (n) n , |
n 0,...,C , |
(5.12) |
C
N C (n);
n 0
C (i) C ( j) , i j.
09.04.2013 |
Модель отдельного звена |
22 |
© Гайдамака Ю.В.
Модель стохастического ранца (2/3)
P(n) P{C (n)} |
(n). |
|
(5.13) |
||
|
|
|
n C (n) |
|
|
|
K |
|
|
|
|
nP(n) dk ak P(n dk ), |
n 0,...,C . |
(5.14) |
|||
|
k 1 |
|
|
|
|
0, n 0; |
|
|
|
||
|
|
|
|
||
1, n 0; |
|
|
|
||
h(n) |
|
|
(5.15) |
||
1 K |
|
|
|
||
|
|
dk ak h(n dk ), n 1,...,C. |
|
||
n k 1
09.04.2013 |
Модель отдельного звена |
23 |
© Гайдамака Ю.В.
Модель стохастического ранца (3/3)
Нормирующая константа
C |
|
G(N ) h(n) . |
(5.16) |
n 0
Вероятность блокировки установления соединения k-класса
C
h(n)
Bk |
n C dk 1 |
, k K . |
(5.17) |
|
G(N ) |
||||
|
|
|
Среднее число занятых единиц емкости звена
C
n h(n)
|
|
|
n 1 |
|
|
|
d |
. |
(5.18) |
||||
G(N ) |
||||||
|
|
|
|
|
||
09.04.2013 |
Модель отдельного звена |
24 |
© Гайдамака Ю.В.
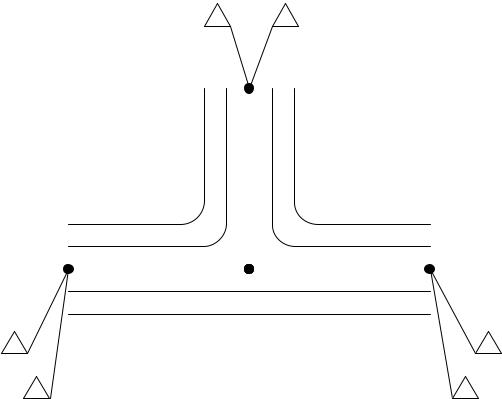
Метод просеянной нагрузки
n* 0,0, 4,0,7,0
|
|
|
|
|
|
|
|
|
|
|
|
|
Будет ли заблокирован запрос |
|
|
|
|
|
|
|
|
|
|
|
|
|
на установление соединения |
|
|
|
|
|
=35 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) 2-класса, поступивший с |
|
d4=5 |
|
|
|
|
|
|
|
|
d2=1 |
|
|
|
|
|
|
|
|
|
|
|
интенсивностью нагрузки a2 ? |
|||||
|
|
|
|
|
|
|
|
|
|
||||
|
d1=1 |
|
|
|
|
|
|
d5=5 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1=30 |
|
|
|
|
C3=40 |
|
|
|
|
б) 3-класса, поступивший с |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
d3=1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d6=5 |
|
|
интенсивностью нагрузки a3 ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
09.04.2013 |
Метод просеянной нагрузки |
25 |
© Гайдамака Ю.В.
|
Случай |
dk |
1, |
k K (1/3) |
|||
Модель Келли: |
|
|
|
|
|
|
|
B(l) {n N : dl (n) Cl }, l L |
|
|
|
(5.19) |
|||
- система событий, l -звено полностью занято; B(l) P(B(l)) |
|||||||
Bk |
B(l), k K |
|
|
|
|
|
|
|
l Lk |
|
|
|
|
|
|
По закону де Моргана |
|
|
|
|
|
||
Bk P(Bk ) P( |
B(l)) 1 P( |
|
|
(l)), k K . |
|||
B |
|||||||
|
l Lk |
|
l Lk |
|
|
|
|
Bk* 1 1 B(l) , k K |
|
|
|
|
(5.20) |
||
l Lk
- условная вероятность блокировки запроса на установление одноканального соединения k-класса при условии, что блокировки на звеньях происходят независимо.
09.04.2013 |
RLA: модель Келли, |
26 |
|
одноканальные соединения |
© Гайдамака Ю.В. |

Случай dk 1, k K (2/3)
B(l) E a(l),Cl , l L ,
где a(l) – интенсивность нагрузки, поступающей на l-звено,
C
C n
E(a,C) aC! an! - 1-я формула Эрланга.
n 0
Интенсивность предложенной нагрузки на l-звено: |
|||
a(l) |
ak |
|
1 B( j) , l L . |
|
k K l |
j Lk \{l} |
|
a(l) - нагрузка на l-звено с учётом «просеивания»:
a(l) ak .
k K l
09.04.2013 RLA: модель Келли,
одноканальные соединения
(5.21)
(5.22)
27
© Гайдамака Ю.В.
Случай dk 1, |
k K (3/3) |
Подставив (5.4) в (5.3), получим систему неявных уравнений |
|
|||
для одноканальных соединений ( dk 1, |
k K ) |
|
||
|
|
|
|
|
B(l) E ak |
1 B( j) ,Cl , l L . |
(5.23) |
||
|
j Lk \{l} |
|
|
|
k K l |
|
|
|
|
Система (5.23) имеет решение по теореме Брауэра как неподвижная точка непрерывного отображения E : 0,1 L 0,1 L . Решение можно получить, например, методом последовательных приближений.
Подставив решение системы (5.23) в (5.20), получаем условную вероятность Bk* .
09.04.2013 |
RLA: модель Келли, |
28 |
|
одноканальные соединения |
© Гайдамака Ю.В. |
Случай |
dk 1, |
k K (1/3) |
Bk* 1 1 B(l) dk , k K |
|
(5.24) |
l Lk |
|
|
- условная вероятность блокировки запроса на установление многоканального соединения k-класса при условии, что блокировки на звеньях происходят независимо.
Интенсивность обслуженной нагрузки на l-звено:
ˆ |
|
dk ak |
1 |
|
B( j) |
dk |
, l |
|
L . |
(5.25) |
|
a(l) |
|
|
|
|
|||||||
|
|
k K l |
j Lk |
|
|
|
|
|
|
|
|
Интенсивность предложенной нагрузки на l-звено:
a(l) |
|
aˆ(l) |
|
1 |
dk ak 1 B( j) dk , l L . |
(5.26) |
|
|
B(l) |
|
|||||
1 |
|
1 B(l) k l |
j L |
|
|||
|
|
|
|
|
K |
k |
|
aˆ(l), a(l) - нагрузки на l-звено с учётом «просеивания»:
aˆ(l) a(l) dk ak
k K l
09.04.2013 RLA: модель Келли,
многоканальные соединения
29
© Гайдамака Ю.В.
Случай dk 1, |
k K (2/3) |
B(l) - решение системы неявных уравнений
для многоканальных соединений ( dk 1, |
k K |
|||||
|
1 |
|
|
|
|
|
B(l) E |
dk ak 1 B( j) dk ,Cl , l |
|||||
1 B(l) |
||||||
|
k K |
l |
j Lk |
|
||
|
|
|
|
|||
)
L . (5.27)
Система (5.27) имеет решение по теореме Брауэра как неподвижная точка непрерывного отображения E : 0,1 L 0,1 L . Единственность решения
доказана Келли, сходимость метода последовательных приближений - Уиттом.
Подставив B(l) в (5.24), получаем условную вероятность Bk* .
09.04.2013 |
RLA: модель Келли, |
30 |
|
многоканальные соединения |
© Гайдамака Ю.В. |
