Дифференциальные уравнения(МТУСИ)2013г

В примерах с 1 по 14 решить задачи в соответствии с условиями варианта задания:

-в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное решение дифференциального уравнения;

-в примере 10 написать общее решение дифференциального уравнения со специальной правой частью, не находя числовых значений неопределенных коэффициентов частного решения;

-в примере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейлора);

-в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.

21.5xy¢¢ = (1 + 2x2 )y¢.

21.6y¢¢ + y¢ + 2 = 0; y (0) = 0, y¢(0) = -2 .

21.71 + (y¢)2 = yy¢¢; y (0) =1, y¢(0) = 0 .

21.8y(IV ) - 2 y¢¢¢ + y¢¢ = 0; y (0) = y¢(0) = 0, y¢¢(0) =1, y¢¢¢(0) = 2 .

21.9y¢¢¢ - 4 y¢ = x2 .

21.10y¢¢¢ + y = 3xe-x + ex (5sinx + cosx).

21.11y¢¢ + 8y¢ +16 y = e-4 x × 3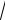x .

21.12 y¢ = x2 y2 + y sin x; y (0) = 0,5.

21.13Записать уравнение кривой, проходящей через точку P (1,2) и обладающей следующим свойством: площадь треугольника, образованного радиусвектором любой точки кривой, касательной в этой точке и осью абсцисс, равна 2.

21.14В электрическую цепь с сопротивлением R =1,5 Ом в течение 2 мин равномерно вводится напряжение (от нуля до 120 В). Кроме того, автоматически вводится индуктивность, так что число генри в цепи равно числу, выра - жающему ток в амперах. Найти зависимость тока от времени в течение первых двух минут опыта.

В примерах с 1 по 14 решить задачи в соответствии с условиями варианта задания:

-в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное решение дифференциального уравнения;

-в примере 10 написать общее решение дифференциального уравнения со специальной правой частью, не находя числовых значений неопределенных коэффициентов частного решения;

-в примере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейлора);

-в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.

Вариант 22

22.4(3x2 y + y3 )dx + (x3 + 3xy2 )dy = 0 .

22.5y¢¢¢ = x .

22.6x2 y¢¢¢ = ( y¢¢)2 .

22.7yy¢¢ + (y¢)2 = 0; y (0) =1, y¢(0) = 2 .

22.8y(IV ) - y = 0; y (0) = y¢(0) = y¢¢(0) = 0, y¢¢¢(0) = -4 .

22.9y¢¢ - 3y¢ + 2 y = xcosx .

22.10y¢¢¢ - y = 5xex + e2 x (6cosx - sinx).

22.11y¢¢ + y = 24sin4 x .

22.13Записать уравнение кривой, проходящей через точку A(2; 0) и обладающей свойством: отрезок касательной между точкой касания и осью Oy имеет постоянную длину, равную 2.

22.14На расстоянии a друг от друга в точках A и B сосредоточены два равных разноименных заряда +q и -q . Приняв точку A за начало координат и направив ось X по линии AB , составить уравнение семейства эквипотенциальных линий электрического поля, создаваемого указанными зарядами.

В примерах с 1 по 14 решить задачи в соответствии с условиями варианта задания:

-в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное решение дифференциального уравнения;

-в примере 10 написать общее решение дифференциального уравнения со специальной правой частью, не находя числовых значений неопределенных коэффициентов частного решения;

-в примере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейлора);

-в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.

23.2 x2dy = (y2 - xy + x2 )dx .

23.13 Записать уравнение кривой, каждая касательная к которой пересекает прямую y =1 в точке с абсциссой, равной удвоенной абсциссе точки касания.

23.14 Электрическая цепь состоит из последовательно соединенных источников тока с э.д.с. E (t ) = E0 sin(wt + j), индуктивности L и емкости C ,

В примерах с 1 по 14 решить задачи в соответствии с условиями варианта задания:

-в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное решение дифференциального уравнения;

-в примере 10 написать общее решение дифференциального уравнения со специальной правой частью, не находя числовых значений неопределенных коэффициентов частного решения;

-в примере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейлора);

-в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.

24.8y¢¢¢ + y¢¢ - 4 y¢ - 4 = 0; y (0) = y¢(0) = 0, y¢¢(0) =12.

24.9y¢¢¢ - 4 y¢ = xe2 x .

24.10y¢¢ - 3y¢ + 2 y = 3x + 5sin2x.

24.11y¢¢ + y¢ = e2 x × 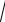1 + e-2 x .

24.12 y¢¢ = x2 + y2 ; y (-1) = 2, y¢(-1) = 0,5.

24.13Записать уравнение кривой, обладающей свойством: если через любую ее точку провести прямые, параллельные осям координат, до пересечения с этими осями, то площадь полученного прямоугольника делится кривой на две части, причем площадь одной из них вдвое больше площади другой.

24.14Сила тока I в цепи с сопротивлением R , индуктивностью L и напряжением U удовлетворяет дифференциальному уравнению

L dI + R × I = kt , dt

где k ,L,R -постоянные. Найти I (t )при начальном условии I( 0 ) = 0 .

В примерах с 1 по 14 решить задачи в соответствии с условиями варианта задания:

-в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное решение дифференциального уравнения;

-в примере 10 написать общее решение дифференциального уравнения со специальной правой частью, не находя числовых значений неопределенных коэффициентов частного решения;

-в примере 12 решить дифференциальное уравнение с помощью формулы

Тейлора (найти первые три ненулевых члена разложения по форм Тейлора);

-в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.

Вариант 25

25.1(xy2 + x)dx + (x2 y - y )dy = 0; y (0) =1.

25.2(x + y - 2)dx - (x - y + 4)dy = 0.

25.3y¢ + 2xy = xe-x2 .

25.4xdx + ydy = xdy - ydx .

x2 + y2

25.5y¢¢ = xex ; y (0) = 0, y¢(0) = 0.

25.6yy¢¢ = (y¢)3 .

25.7 y (1 - lny) y¢¢ + (1 + lny )(y¢)2 = 0; y (0) = y¢(0) =1.

25.8y¢¢¢ + 2 y¢¢ + 9 y¢ +18 y = 0; y (0) =1, y¢(0) = -3, y¢¢(0) = -9.

25.9y¢¢ + 2 y¢ + 5y = e- xsin2x.

25.10y¢¢¢ + 2 y¢¢ + 5y¢ = 4xe- x - 68cos 2x + x.

25.12y¢ = 2xy2 + e3 x ; y (0) =1.

25.13Записать уравнения кривых, для которых длина отрезка, отсекаемого нормалью в точке M (x; y ) на оси Ox , равна y2 / x .

25.14Изолированному проводнику сообщен заряд q0 =1000 CGSE единиц. Вследствие несовершенства изоляции проводник постепенно теряет свой заряд. Скорость потери заряда в данный момент пропорциональна наличному

заряду проводника. Какой заряд останется на проводнике по истечении времени t =10 мин, если за первую минуту потеряно 100 CGSE единиц?

В примерах с 1 по 14 решить задачи в соответствии с условиями варианта задания:

-в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное решение дифференциального уравнения;

-в примере 10 написать общее решение дифференциального уравнения со специальной правой частью, не находя числовых значений неопределенных коэффициентов частного решения;

-в примере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейлора);

-в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.

Вариант 26

26.1 tgxsin2 ydx + cos2 xctgydy = 0.

26.5x4 y¢¢ + x3 y¢ =1; y(1) = 0, y¢(1) = 0 .

26.6y¢¢tgx = y¢ +1.

26.8y(V ) - 6 y(IV ) + 9 y¢¢¢ = 0; y (0) = y¢(0) = y¢¢(0) = y¢¢¢(0) = 0, y(IV ) (0) = 27.

26.9y¢¢ + y¢ = x2 .

26.10y¢¢¢ - 4 y¢ = 24e2 x - 4cos2x + 8sin2x.

26.11y¢¢ + y = ctgx.

26.12y(4) = xy + y¢x2 ; y (0) = y¢(0) = y¢¢(0) = y¢¢¢(0) =1.

26.13Записать уравнения кривых, для которых длина отрезка, отсекаемого нормалью в точке M (x; y ) на оси Oy , равна x2 / y .

26.14Пуля входит в брус толщиной 12 см со скоростью 200 м/с, а вылетает из него, пробив его, со скоростью 60 м/с. Брус задерживает движение пули, сила сопротивления которого пропорциональна квадрату скорости движения. Найти время движения пули через брус.

В примерах с 1 по 14 решить задачи в соответствии с условиями варианта задания:

-в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное решение дифференциального уравнения;

-в примере 10 написать общее решение дифференциального уравнения со специальной правой частью, не находя числовых значений неопределенных коэффициентов частного решения;

-в примере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейлора);

-в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.

Вариант 27

27.1(1 + ex ) yy¢ = ex ; y (0) =1.

27.2xdy - ydx = ydy.

27.3xy¢ - 2x2 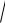y = 4 y.

27.4(3x2 + 6xy2 )dx + (6x2 y + 4 y3 )dy = 0.

27.5y¢¢¢ = x sin x; y (0) = y¢(0) = y¢¢(0) = 0 .

27.6x2 y '' = ( y ')2

27.7 y¢¢ = y¢ ; y (0 )=1, y¢(0 )= 2. y

27.8y¢¢¢ + 2 y¢¢ + y¢ = 0; y (0) = 0, y¢(0) = 2, y¢¢(0) = -3.

27.9y¢¢ + 4 y = xsin2x .

27.10y¢¢¢ + 4 y¢ = 3ex + sin2x - 7cos2x.

27.11y¢¢ + y = secx.

27.12y¢ = x + ey ; y (0) = 0.

27.13В точке с ординатой 2 кривая наклонена к оси Oy под углом 45°. Любая ее касательная отсекает на оси абсцисс отрезок, равный по длине квадрату ординаты точки касания. Записать уравнение данной кривой.

27.14Круглый цилиндрический бак с вертикальной осью, диаметром 2R и высотой H наполнен водой. Из бака вода вытекает через круглое отверстие диаметром 2a в дне бака. Определить время опорожнения бака.

В примерах с 1 по 14 решить задачи в соответствии с условиями варианта задания:

-в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное решение дифференциального уравнения;

-в примере 10 написать общее решение дифференциального уравнения со специальной правой частью, не находя числовых значений неопределенных коэффициентов частного решения;

-в примере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейлора);

-в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.

Вариант 28

28.1 3ex tgydx + 1 - ex dy = 0. cos2 y

28.22x3 y¢ = y(2x2 - y2 ).

28.3x2 + xy¢ = y; y (1) = 0.

28.5x2 y¢¢ + xy¢ =1.

28.6(x +1) y¢¢ - (x + 2) y¢ + x + 2 = 0.

28.7y¢¢ =1+ (y¢)2 ; y (0) = y¢(0) = 0.

28.8y¢¢¢ - y¢¢ - y¢ + y = 0; y (0) = -1, y¢(0) = 0, y¢¢(0) =1.

28.9y¢¢ - 4 y¢ + 3y = xex .

28.10y¢¢¢ + y¢¢ = x2 - 3 + ex (6sinx + 3cosx).

28.11y¢¢ - y =1/ (ex + 2).

28.12 y¢¢¢ = y¢¢ + ( y¢)2 + y3 + x; y (0) =1, y¢¢(0) = 0,5.

28.13Кривая y = y(x) проходит через начало координат. Середина отрезка ее нормали, заключенного между любой точкой кривой и осью абсцисс, лежит на параболе y2 = ax . Составить уравнение указанной кривой.

28.14Моторная лодка движется в спокойной воде со скоростью v0 = 20 км/ч. На полном ходу ее мотор выключается и через 40 с после этого скорость лодки уменьшается до v1 = 8 км/ч. Сопротивление воды пропорционально скорости движения лодки. Определить скорость лодки через 2 мин после остановки мотора.

В примерах с 1 по 14 решить задачи в соответствии с условиями варианта задания:

-в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное решение дифференциального уравнения;

-в примере 10 написать общее решение дифференциального уравнения со специальной правой частью, не находя числовых значений неопределенных коэффициентов частного решения;

-в примере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейлора);

-в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.

Вариант 29

29.1y¢ + cos(x + 2 y) = cos(x - 2 y); y (0) = p / 4.

29.2xy¢ = y + y2 - x2 .

29.3x( y¢ - y ) = ex .

29.8y(IV) + 5 y¢¢ + 4 y = 0; y (0) =1, y¢(0) = 4, y¢¢(0) = -1, y¢¢¢(0) = -16.

29.9y¢¢ + 2 y¢ + 2 y = e- xcosx.

29.10y¢¢¢ + y¢ = 2ex + 2sinx - 6cosx.

29.11y¢¢ + 4 y =1/ sin2x.

29.12 y¢ = y cos x + 2cos y; y (0) = 0.

29.13Кривая y = y(x) проходит через точку (0;1) и обладает тем свойством, что в

каждой ее точке тангенс угла касательной к этой кривой равен удвоенному произведению координат точки касания. Найти кривую y = y(x) .

29.14Определить время, необходимое для установления одинакового уровня жидкости в сообщающихся сосудах, если в начальный момент уровень

жидкости в первом сосуде находился на высоте h1 от отверстия, а во втором

– на высоте h2 (h1 > h2 ).Площадь горизонтального сечения первого сосуда равна S1 , второго - S2 , а площадь отверстия – s.

В примерах с 1 по 14 решить задачи в соответствии с условиями варианта задания:

-в примерах 1- 9, 11 найти общее решение (общий интеграл) или частное решение дифференциального уравнения;

-в примере 10 написать общее решение дифференциального уравнения со специальной правой частью, не находя числовых значений неопределенных коэффициентов частного решения;

-в примере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейлора);

-в примерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.

Вариант 30

30.1yy¢ + ey = 0; y (1 )= 0. x

30.2y¢ = y2 - 2.

x2

30.5y¢¢ =1/ (1 + x2 ); y (0) = y¢(0) = 0

30.6y¢¢(1 + ln x )+ yx' = 2 + ln x; y (1 )= 12 , y '(1 )=1

30.7y¢¢ =1/ 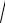y; y (0) = y¢(0) = 0.

30.8y(IV) +10 y¢¢ + 9 y = 0; y (0) =1, y¢(0) = 3, y¢¢(0) = -9, y¢¢¢(0) = -27.

30.9y¢¢ + y¢ = cos2 x.

30.10y¢¢¢ - y¢ = (2x - 5)ex + 6cosx - 5sinx.

30.11y¢¢ - y¢ = ex / (ex +1).

30.12y¢¢¢ = yex - x( y¢)2 ; y (0) =1, y¢(0) = y¢¢(0) =1.

30.13 Кривая проходит через начало координат и лежит в полуплоскости y ³ 0 . Каждый прямоугольник, ограниченный осями координат и перпендикуля - рами к ним, делится на две части, причем площадь части прямоугольника, находящейся под кривой, в 2 раза меньше площади части прямоугольника, находящейся над кривой. Найти уравнение кривой.

30.14 Цепь длиной L = 4 м соскальзывает с гладкого горизонтального стола. В начальный момент движения со стола свисал конец цепи длиной а = 0,5 м. Пренебрегая трением, найти время соскальзывания всей цепи по столу.