
В) имеет эллиптическую поляризацию, бежит в сторону отрицательных Z , вращение вектора со стороны наблюдателя происходит вправо;
*С) распространяется в сторону отрицательных Z, имеет правую круговую поляризацию; D) распространяется в сторону отрицательных Z, имеет левую круговую поляризацию.
|
20. (НТ2). (З). Компоненты электрического поля в электромагнитной волне имеют вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ex |
ex Ex0 sin( t ky) |
Ez |
ez Ez0 cos( t ky) . |
При этом волна: |
|
А) распространяется вдоль OY, имеет правую эллиптическую поляризацию; |
|
В) распространяется вдоль OY, имеет правую круговую поляризацию; |
|
*С) распространяется вдоль OY, имеет левую эллиптическую поляризацию; |
|
D) распространяется вдоль OY, имеет левую круговую поляризацию. |
|
21. (НТ2). (З). Если в бегущей вдоль оси Z волне между компонентами колеблющегося в |
|
|
|
|
|
|
|
A2 (z,t) |
|
Ay2 (z,t) |
1, то это: |
|
волне вектора A имеется связь вида |
x |
|
|
|
E2 |
E2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xm |
|
ym |
|
|
А) только электромагнитная волна с круговой или эллиптической поляризацией для |
|
|
|
|
|
|
|
|
|
|
|
|
|
которой A E(z,t) |
или A |
H (z,t) ; |
|
|
|
|
|
*В) любая поперечная векторная волна с круговой или эллиптической поляризацией; С) любая поперечная векторная волна с эллиптической поляризацией;
D) произвольная векторная волна (продольная, поперечная, продольно поперечная) с эллиптической поляризацией.
|
|
|
|
|
|
|
|
|
|
22. (НТ2). (З). Если компоненты вектора H в электромагнитной волне описываются |
уравнениями |
|
|
|
|
Hx ex Hm sin( t kz) |
H y ey Hm cos( t kz) , то: |
|
А) |
|
|
|
|
|
и волна имеет левую круговую поляризацию; |
|
v |
e v |
|
|
В) |
p |
|
|
z |
p |
|
|
|
|
v p |
ez v p |
и волна имеет правую круговую поляризацию; |
|
|
|
|
|
|
|
|
и волна имеет правую круговую поляризацию; |
|
*С) v |
|
e v |
|
|
|
|
p |
|
z |
|
p |
|
|
|
D) v p |
ez v p , но для определения поляризации необходимы соотношения Ex |
, Ey . |
23. (НТ1).(С ). Волне, указанной в левом столбике, соответствует следующее значение вектора Пойнтинга ( ) в заданном элементе пространства
А) Линейно поляризованная волна |
|
|
|
|
|
|
|
|
А) |
max |
const |
|
|
|
|
|
|
|
|
|
|
|
В) Волна с левой круговой поляризацией |
|
|
|
|
|
|
|
|
В) max sin2 t |
С) Волна с правой круговой поляризацией |
|
|
|
|
|
|
|
С) |
min max |
D) Эллиптически поляризованная волна |
|
|
|
|
|
|
|
|
D) 0,5 max (1 cos 2t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E) |
|
max |
cos2 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: А – В,D,E; |
|
B,C – A; |
D – C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ix , |
|
|
|
I y . |
24. (НТ1). Часто записывают интенсивность волны с E |
ex |
|
E |
ey |
Интенсивность волн от теплового источника равна : |
|
|
|
|
|
|
|
|
|
|
А) I Ix |
или I I y , причем Ix I y . ) I Ix |
I y , где Ix , I y |
|
могут иметь любые значения; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*С) I I |
|
I |
|
|
|
I |
|
|
D) I I 2 |
I 2 |
I |
|
|
|
|
I |
|
|
|
|
|
x |
y |
, а I |
x |
y |
; |
x |
2 |
, т.к. I |
x |
y |
|
|
|
|
|
|
|
|
|
|
x |
y |
|
|
|
|
|
|
|
|
|
|

25. (HТ2). (З). Если в спектре волнового поля имеют место частоты в интервале , то время когерентности k для наблюдения квазистационарной картины интерференции можно оценить по формуле… (Выбрать все неверные ответы)
А) |
|
|
|
|
|
1 |
; |
*B) |
|
|
|
; |
* C) |
|
|
|
; |
*D) |
|
|
|
|
. |
k |
|
|
|
k |
( )2 |
k |
|
2 |
k |
v |
ph |
2 |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
В этих формулах - интервал длин волн в спектре; ν – среднее значение частоты.
26.(HT1). (З). За время t наблюдения интерференции в точке М случайное отклонение сдвига фаз = /4. В этом случае интерференция:
A. не будет наблюдаться, т. к. t > tкогер; *B. будет наблюдаться, т. к. t < tкогер; C. не будет наблюдаться, т. к. t = tкогер; D. будет наблюдаться, т. к. t> tкогер.
27.(HT2). (З). За время наблюдения интерференции t в точке М случайное отклонение сдвига фаз волн δφ = (4/3)π. В этом случае в точке М интерференция:
A.будет наблюдаться, т. к. t<τ когер;
B.везде будет наблюдаться, т. к. t=τ когер; *C. не будет наблюдаться, т. к. t>τ когер;
D.не будет наблюдаться, т. к. t<τ когер.
28. (HТ1). (З). От двух когерентных источников электромагнитные волны попадают в точку «А» (рис.) . Условие максимума и минимума амплитуды колебаний в т. «А» имеет вид
E E1m E2m |
|
(N1 N2 )(r1 r2 ) m 0 |
|
|
|
|
А) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m 1 |
|
|
0 - длина волны в |
E | E |
|
|
E |
2m |
| |
(N N |
2 |
)(r r ) |
|
|
|
, где m 0, 1, 2,... |
|
|
|
|
|
1m |
|
|
|
1 |
|
|
|
|
1 |
|
|
2 |
|
|
2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вакууме; N - коэффициент преломления. |
|
|
|
|
|
|
E E1m E2m |
|
|
N1r1 N2r2 m 0 |
|
|
|
|
|
|
*В) E | E |
|
E |
|
| |
|
N r N |
|
r |
|
2m 1 |
, где |
m 0, 1, 2,... |
|
|
|
|
|
|
|
|
|
1m |
|
2m |
|
|
1 1 |
|
|
|
2 |
2 |
|
|
|
2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E E1m E2m |
|
|
|
N1r1 N2r2 m |
|
|
|
|
|
|
С) E | E |
E |
| |
|
|
N r N |
r |
2m 1 |
, где |
m 0, 1, 2,..., |
- длина волны в |
|
|
|
|
|
1m |
|
|
2m |
|
|
|
1 1 |
|
2 |
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рассматриваемой среде; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E E1m E2m |
|
|
|
r1 r2 m(1 2 ) |
|
|
|
|
|
|
D) |
|
|
|
|
|
|
|
|
|
2m 1 |
|
|
|
|
|
|
|
|
1, 2 - длины волн в |
E | E |
E |
| |
|
|
r r |
|
|
|
|
|
|
|
|
|
( ), где |
|
m 0, 1, 2,... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1m |
|
|
2m |
|
|
|
1 |
2 |
|
|
|
|
|
2 |
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
каждой из сред.
29. (HТ2).(С). Конструктивной и деструктивной интерференции двух когерентных волн с амплитудами в точке наблюдения E1m, E2m соответствует следующее соотношение между суммарной интенсивностью и амплитудой поля (левый столбик) и выражениями в правом столбике:
A) E1m E2m , |
|
|
| E1m E2m | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B) |
E2 |
E2 |
, |
|
| E2 |
E2 |
|
| |
|
А) интенсивность |
|
1m |
|
2m |
|
|
|
1m |
|
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I 2 I 2 , |
|
|
| I 2 I 2 |
|
|
|
|
|
|
|
C) |
|
|
| |
|
|
|
|
|
|
|
1 |
|
2 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D) ( I I |
2 |
)2 , ( I I |
2 |
)2 |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
В) амплитуда поля Ответ: А-D; B-A.
30. (HТ2). (З). В опыте Юнга на две щели падает монохроматический свет с длиной
волны λ и частотой ν от удалѐнного источника, для которого время когерентности τК. Наибольшее число максимумов на экране определяется формулой:
A) m ≤ τК ν; |
B) m ≤ 1/(τК ν); |
*C) m ≤ cτК/ λ; |
D) m ≤ λ /cτК. |
31. (HТ2). (З). В точку M приходят две волны y1 = Acos(ωt+kx) и y2 = Acos(ωt+kx+φ). В
этой точке наблюдается максимальная интенсивность, если:
A. φ = mπ/2; где m=0,1,2…; |
B. φ = (2m+1)π/2; где m=0,1,2…; |
C. *φ = 2mπ; где m=0,1,2…; |
D. φ = (2m+1)π; где m=0,1,2… . |
32. (HТ2). (З). Два синфазных источника находятся на раcстоянии “a” друг от друга и
излучают электромагнитные волны в направлении θ на удалѐнный приѐмник. Разность фаз между волнами в месте расположения приѐмника ∆φ равна:
|
A. ∆φ = (2π/λ) a cosθ; |
|
θ |
|
B. *∆φ = (2aπ/λ) sinθ; |
|
|
|
|
|
C. ∆φ = (2πλ/a) sinθ ; |
а |
|
D. ∆φ = mπθNa. |
|
|
|
|
|
|
|
33. (НT1). (З). Тонкая плѐнка одинаковой толщины освещается светом с частотами
ν1 и ν2 < ν1. В проходящем свете в точке М наблюдается максимум интенсивности волны с частотой только ν1. В точке К будет наблюдаться максимум интенсивности волны с частотой:
A. *ν = ν1 ; |
В)ν = ν2 ; С) ν 2 < ν < ν1 ; |
|
|
D) Зависит от расстояния КМ. |
● |
● |
|
|
|
|
К |
М |
34. (HТ3). (З). Две одинаковые радиомачты, удалѐнные друг от друга на расстояние d,
работают в противофазах на частоте ν. Максимумы излучения будут наблюдаться в
направлениях: |
|
*A. Sinθ = (2m-1)λ/2d; где m=1,2,3…; |
B. Sinθ = mλ/d; где m=1,2,3…; |
C. Sinθ = mλ/2d; где m=1,2,3…; |
D. Sinθ = (2m-1)λ/d; где m=1,2,3… . |
183
35. (HT3). (З). Параллельный пучок монохроматического света с длиной волны λ
падает на две щели шириной а и промежутком между ними b. Минимумы интенсивности света наблюдаются в направлениях:
A. |
*sinθ1 = λ(2m+1)/(2(a+b)); sinθ 2= λm/a; |
B. |
sinθ1 |
= mλ/(2b); |
sinθ2 = λ(2m+1)/(2a); |
C. |
sinθ1 |
= mλ/(a+b); |
sinθ2 = λ(2m+1)/(2a); |
D. |
только для sinθ = λm/a. |
36.(HТ1). (З). В закрытой с концов трубе длиной L заперт столб воздуха, в котором возбуждается стоячая волна основного тона. В трубе для смещения слоѐв среды возникнут:
*А. Одна пучность и два узла; В. Две пучности и один узел;
C.Две пучности и два узла;
D.Одна пучность и один узел.
37. (HТ1). (З). Если волновые функции бегущих навстречу волн
1 |
Acos(t kx), |
2 Acos(t kx) , то волновая функция стоячей волны имеет вид: |
|
A) Acos kx cos t; |
B) 2Acos kx sin t; |
|
*C) 2Acos kx cos t; |
D) 2Asin kx sin t. |
38. (HТ1). (З). Если волновые функции бегущих навстречу волн |
1 |
Asin(t kx), |
2 Asin(t kx) , то волновая функция стоячей волны имеет вид : |
|
A) Acos kx cos t; |
*B) 2Acos kx sin t; |
|
C) 2Acos kx cos t; |
D) 2Asin kx sin t. |
39. (HТ1). (З). Если волновые функции бегущих навстречу волн |
1 |
Acos(t kx), |
2 Acos((t kx) ) , то волновая функция стоячей волны имеет |
вид: |
|
|
|
|
A) Acos kx cos t; |
B) 2Acos kx sin t; |
C) 2Acos kx cos t; *D) 2Asin kx sin t.
40. (HТ2). (З). Электрическое поле стоячей электромагнитной волны описывается функцией Ex 2E0 cos kz cost . Соответствующее выражение для магнитного поля волны
имеет вид: |
|
|
*A) H y 2H0 sin kz sin t; |
B) Hz |
2H0 sin kz sin t; |
C) H y 2H0 sin kz cos t; |
D) H y |
2H0 cos kz sin t. |
41. (HТ2). (З). Электрическое поле стоячей электромагнитной волны описывается функцией Ex 2E0 cos kz sin t . Соответствующее выражение для магнитного поля волны
имеет вид: |
|
A) H y 2H0 sin kz sin t; |
B) Hz 2H0 sin kz sin t; |
*C) H y 2H0 sin kz cos t; |
D) H y 2H0 cos kz sin t. |
42. (HТ2). (З). Стоячая электромагнитная волна образуется при сложении двух встречных волн, электрические поля которых описываются функциями
E1x E0 sin(t kz), E2x E0 sin(t kz) . Соответствующие выражения для магнитных полей этих волн имеют вид:
A) B1y
*B) B1
C) B1y D) B1z
B0 cos(t kz), B2 y B0 cos(t kz);
yB0 sin(t kz), B2 y B0 sin(t kz);
B0 sin(t kz), B2 y B0 sin(t kz);
B0 sin(t kz), B2 z B0 sin(t kz).
43. (HТ2). (З). Стоячая электромагнитная волна образуется при сложении двух встречных волн, электрические поля которых описываются функциями
E1x E0 sin(t kz), E2x E0 sin(t kz) . Соответствующие выражения для магнитных полей этих волн имеют вид:
A) B1y |
B0 cos(t kz), |
B2 y |
B0 cos(t kz); |
B) B1y |
B0 sin(t kz), |
B2 y |
B0 sin(t kz); |
*C) B1y B0 sin(t kz), B2 y B0 sin(t kz); D) B1z B0 sin(t kz), B2 z B0 sin(t kz).
44. (HТ2). (З). В дальней зоне угловая ширина главных максимумов ( , при 1)во многолучевой интерференции N лучей равна
|
*A) |
2 |
; |
B) |
42 |
; |
C) |
2d |
; |
D) |
2 |
|
dN |
(dN )2 |
N |
dN 2 |
|
|
|
|
|
|
|
|
45. (HТ2). (З). Стоячая электромагнитная волна образуется при сложении двух встречных волн, электрические поля которых описываются функциями
E1x E0 cos(t kz), E2x E0 cos(t kz) . Соответствующие выражения для магнитных
полей этих волн имеют вид: |
|
*A) B1y B0 cos(t kz), |
B2 y |
B0 cos(t kz); |
B) B1y |
B0 sin(t kz), |
B2 y B0 sin(t kz); |
C) B1y |
B0 sin(t kz), |
B2 y |
B0 sin(t kz); |
D) B1z |
B0 sin(t kz), |
B2 z B0 sin(t kz). |
46. (HТ2). (З).Электрическое поле стоячей электромагнитной волны описывается функцией Ex 2E0 sin kz cos t . Соответствующее выражение для магнитного поля волны
имеет вид: |
|
A) H y |
2H0 sin kz sin t; |
B) Hz 2H0 sin kz sin t; |
C) H y |
2H0 sin kz cos t; |
* D) H y 2H0 cos kz sin t. |
47. (HТ1) (З). На рисунке изображѐн мгновенный
снимок электрического поля стоячей электромагнитной волны. Объѐмные плотности магнитной энергии в точках 1 и 2 в данный момент времени равны:
A.w1=wmax ; w2=0 ;
B.w2=wmax ; w1=0 ;
C.w1=w2=wmax ;
*D. w1=w2=0.
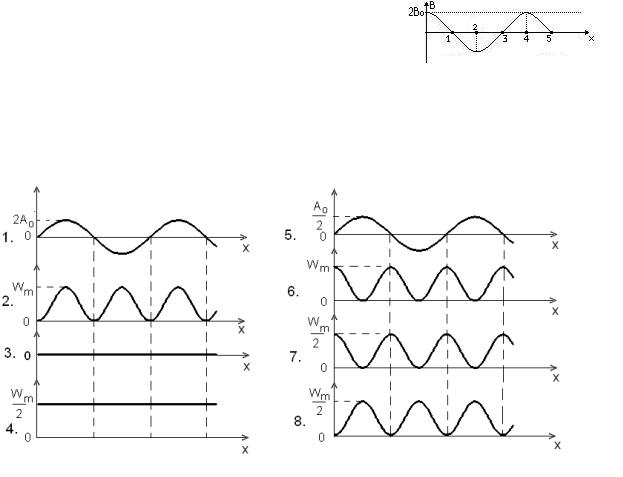
48. (HТ1). (З). На рисунке изображѐн мгновенный
снимок магнитного поля в стоячей электромагнитной волне. Пучности напряженности электрического поля в данный момент наблюдается в точках:
A.1, 3, 5;
B.0, 2, 4;
C.0, 4 ;
*D. E=0 при любых значениях Х.
Рисунок к вопросам № 49 - 53.
49. (HТ2). (О). На рис. 1 приведено распределение амплитуды электрического поля в стоячей волне в некоторый момент времени t . A0 - амплитуда поля в бегущей волне; Wm -
максимальная плотность энергии. Распределение плотности электрической и магнитной энергии в стоячей волне показано на рисунках:
Ответ: 2 и 3.
50. (HТ2). (О). На рис. 1 приведено распределение амплитуды магнитного поля в стоячей волне в некоторый момент времени t . A0 - амплитуда поля в бегущей волне; Wm -
максимальная плотность энергии. Распределение плотности электрической и магнитной энергии в стоячей волне показано на рисунках:
Ответ: 3 и 2.
51. (HТ2). (О). На рис. 3 приведено распределение амплитуды электрического поля в стоячей волне в некоторый момент времени t . A0 - амплитуда поля в бегущей волне; Wm -
максимальная плотность энергии. Распределение плотности электрической и магнитной энергии в стоячей волне показано на рисунках:
Ответ: 3 и 2
52. (HТ2). (О). На рис. 5 приведено распределение амплитуды магнитного поля в стоячей волне в некоторый момент времени t . A0 - амплитуда поля в бегущей волне; Wm -
максимальная плотность энергии. Распределение плотности электрической и магнитной энергии в стоячей волне показано на рисунках:

Ответ: 7 и 8
53. (HТ2). (О). На рис. 5 приведено распределение амплитуды электрического поля в стоячей волне в некоторый момент времени t . A0 - амплитуда поля в бегущей волне; Wm -
максимальная плотность энергии. Распределение плотности магнитной и плотности электрической энергии в стоячей волне показано на рисунках… Ответ: 7 и 8.
54. (HТ1). (З). На рисунке изображѐн мгновенный
снимок стоячей упругой волны. При этом соответствующие скорости колебаний частиц в точках B и C равны:
A.Vв=Vm ; Vc=0;
B.Vc=Vm ; Vв=0; *C. Vc=Vв=0;
D. Vc=Vв=Vm.
55. (HT1. (З). Волны E1Y=E0sin(ωt-kx) и E2Y=E0sin(ωt+kx) образуют электрическое
поле в стоячей электромагнитной волне. Амплитуда напряженности электрического поля имеет вид:
A.Em=|2E0cos(ωt-kx)|;
B.Em=|2E0sinkx|;
C.Em=const;
*D. Em=|2E0coskx|.
56.(HT1). (З). В трубе длиной L, открытой с одного конца возбуждаются стоячие
волны, соответствующие 2ой гармонике. Места, в которых кинетическая энергия частиц воздуха в трубе имеет наибольшее значение, соответствуют точкам:
*A. 2,4; B. 1,2,3,4; C. 1,3;
D. одинакова на всей протяжѐнности трубы.
57.(HT2). (З). На рисунке изображѐн мгновенный
снимок стоячей волны. При этом скорости колебательного движения в точках 1 и 2 равны:
A. V1=Vmax ; V2=0.5Vmax; *B. V1=V2=0;
C.V1=V2=Vmax;
D.V1=0 ; V2=0.5Vmax.
58. (HТ2). (З). Стоячая электромагнитная волна образуется при сложении двух
встречных волн, электрические поля в которых описываются функциями: E1X=E0cos(ωt-kz) и E2X=E0cos(ωt+kz). Магнитные поля в этих волнах должны описываться функциями:
*A. B1Y=B0cos(ωt-kz) и B2Y=-B0cos(ωt+kz);
B.B1Y=B0sin(ωt-kz) и B2Y=-B0sin(ωt+kz);
C.B1Z=B0cos(ωt-kz) и B2Z=B0sin(ωt-kz);

D. B1Z=B0cos(ωt-kz) и B2Z=-B0cos(ωt+kz).
59. (НT1). (З). На рисунке изображен мгновенный
снимок cтоячей волны. Разность фаз между колебаниями в точках 1 и 2 равна:
A. 0; |
B. π / 4 ; |
C. 2π / 3; |
*D. π. |
60.(HT1). (З). Волновая функция стоячей электромагнитной волны может иметь
вид:
A. EY=2E0coskx*cosωt ; BY=2B0coskx*cosωt B. EZ=2E0sinky*sinωt ; BY=2B0sinkz*sinωt *C. EX=2E0coskz*cosωt ; BY=2B0sinkz*sinωt D. EZ=2E0sinkx*sinωt ; BY=2B0cosky*cosωt
61.(HT1). (З). На рисунке изображен мгновенный
снимок стоячей волны. Разность фаз между колебаниями в точках 1 и 2 равна:
A.0;
B.π /4;
C.3π /4;
*D. 2π.
62.(HT2). (З). На рисунке изображен мгновенный
снимок магнитного поля в стоячей электромагнитной волне. Места, в которых энергия электрического поля
может принимать наибольшее значения соответствуют точкам:
*A. 2, 6, 10; B. 0, 2, 8;
C. 0, 2, 4, 6, 8, 10;
D. энергия электрического поля одинакова во всех точках.
63.(HT1). (З). Стоячая волна образуется при сложении 2-х волн:
A. y1=A1cos(ωt-kx) и y2=A2cos(ωt-kx+π/2;) B. y1=A1cos(ω1t-kx) и y2=A2cos(ω2t+kx);
C. z1=Acos(ωt-kx) и z2=Acos(ωt+ky); *D. y1=Acos(ωt-kx) и y2=Acos(ωt+kx+π).
64.(HТ2). (З). На рисунке изображен мгновенный снимок
упругой стоячей волны. Объѐмная плотность полной механической энергии (Р) в точках В и С в данный момент времени равна:
*A. PB=Pmax ; PC=0; B. PB=0 ; PC=Pmax; C. PB=PC=0;
D. PB=PC=Pmax
65. (HT1). (З). На рисунке изображен мгновенный
снимок электрического поля в стоячей

электромагнитной волне. Узлы магнитной индукции этой волны наблюдаются в точках:
A.1,3,5,7;
B.2, 6 ;
C.1, 2, 3, 4, 5, 6, 7; *D. 2, 4, 6.
66. (HT2). (З). На рисунке изображен мгновенный снимок
стоячей упругой волны, с амплитудой пучности 2А0 в момент времени t=0. График этой волны через четверть периода имеет вид:
C. D.
67. (HT1). (З). Расстояние между двумя точками стоячей
электромагнитной волны Х = λ /3. Разность фаз между колебаниями напряженности электрического поля этой
волны равна: |
|
A. Δφ = π /3; |
*B. Δφ = 0; |
C. Δφ = 2π /3; |
D. Δφ = π. |
68. (HT1). (З). В открытой с двух концов трубе длиной L
образовалась стоячая волна, соответствующая основному тону. Плотность потенциальной энергии принимает наибольшее
значение в точках (точке): |
|
|
A. 1, 5; |
B. 2, 4; |
*C. 3; |
D. 1, 3, 5 |
69. (HТ1). (З). При «падении» упругой волны на границу двух сред (из 1 в 2), ее отражение с потерей полуволны происходит при условии:.
A)) cs1 cs2 ; B) cs1 cs2 ; *C) 1cs1 2cs2 ; *D)z2 z1
70. (HТ1). (З). При падении упругой волны на границу среды с волновым сопротивлением z волна:
А) полностью отражается и на границе образуется пучность; *В) полностью отражается с потерей полуволны и на границе образуется узел;
С) полностью отражается без потери полуволны и на границе образуется узел; D) частично отражается с потерей полуволны и на границе поле существенно увеличивается (образуется пучность).
71. (HТ2) (З). При падении электромагнитной волны из среды с большим волновым
сопротивлением в среду с меньшим волновым сопротивлением фаза поля E при отражении от границы:

|
|
|
|
|
А) сохраняется (вектор E |
в падающей и отраженной волне имеет одинаковое |
направление); |
|
|
|
|
|
|
|
*В) происходит потеря полуволны ( E |
E |
); |
|
пад |
отр |
|
С) потеря полуволны наблюдается для H ; |
|
D) потеря полуволны происходит и для E |
и для H . |
72. (HТ1). (З). Если в точке наблюдения интерферируют N лучей, то амплитуда |
колебаний: |
|
|
|
|
А. не изменяется; |
|
*B. Увеличивается в N раз; |
С. Увеличивается в N2 раз; |
D. Уменьшается в N2 раз. |
73. (HТ1). (З). Если в точке наблюдения амплитуда колебаний увеличивается в N
раз, то число интерферирующих лучей равно:
A. 
 N ; *B. N; C. N 2; D. нельзя определить.
N ; *B. N; C. N 2; D. нельзя определить.
74. (HТ1). (З). Положение главных максимумов при многолучевой интерференции
определяется условием: |
|
|
|
A. Δφ =(π-1)m/2; |
B. Δφ =2π(m-1/2); |
*C. Δφ =2πm; |
D. Δφ =λm. |
Здесь Δφ – сдвиг фазы между соседними лучами. |
|
|
75. (HТ2). (З). Если в точке наблюдения интерферируют N лучей, то число |
минимумов интенсивности равно: |
|
|
A. N; |
*B. N-1; |
C. N/2; |
D. 2N. |
|
|
76. (HТ2). (З). Антенна состоит из 4-х синфазных когерентных источников,
расположенных на одной прямой на расстоянии а друг от друга. Разность фаз между волнами от соседних источников в направлении на первый минимум интенсивности
равна: |
|
|
|
А) π/8; |
В) π/4; |
* С) π/2; |
D) π. |
77. (HТ1). (З). Угoл, под которым виден первый минимум интерференции волн с длиной волны λ от N источников, расположенных на расстоянии d друг от друга на одной прямой, в дальней зоне, равен:
|
*A) sin |
|
; |
B) sin |
|
; |
C) sin |
N |
; |
D) 2 = |
|
; |
|
Nd |
dN 2 |
d |
Nd |
|
|
|
|
|
|
|
|
|
3.3.Задачи
1.(НТ2). (О). Электрическое поле электромагнитной волны в среде с 1 изменяется по закону E E0 cos(1,5 1014 t 106 x) . Диэлектрическая проницаемость среды равна:
Ответ: 4
2. (НТ1). (О). Дисперсионное уравнение имеет вид ak 2 bk , где a и b - const . Групповая скорость uгр равна:
*Ответ: 2ak+b












