vse_krome_dvukh_voprosov

2. Произведение неопределенности энергии частицы на неопределенность времени ее измерения не меньше постоянной Планка:

Постулаты Бора:

1. B устойчивом атоме электрон может двигаться лишь по особым, стационарным орбитам, не излучая при этом электромагнитной энергии

2.Излучение света атомом происходит при переходе атома из стационарного состояния с большей энергией

Ek в стационарное состояние с меньшей энергией Еn. Энергия излученного фотона равна разности энергий стационарных состояний:

Правило квантования орбит Бора:

На длине окружности каждой стационарной орбиты укладывается целое число n длин волн де Бройля,

соОтветствующих движению электрона

Физический смысл волновой функции

В координатном представлении волновая функция зависит от координат (или обобщѐнных координат) системы. Физический смысл приписывается квадрату еѐ

модуля , который интерпретируется как плотность вероятности (для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами в момент времени :

.

Тогда в заданном квантовом состоянии системы, описываемом волновой

функцией , можно рассчитать вероятность того, что частица будет обнаружена в любой области конфигурационного пространства конечного объема

Следует также отметить, что возможно измерение и разницы фаз волновой функции, например, в опыте Ааронова — Бома.

Условия регулярности волновой функции

Вероятностный смысл волновой функции накладывает определенные ограничения, или условия, на волновые функции в задачах квантовой механики. Эти стандартные условия часто называют условиями

регулярности волновой функции.

1. Условие конечности волновой функции. Волновая функция не может принимать бесконечных

значений, таких, что интеграл 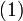станет расходящимся. Следовательно, это условие требует, чтобы волновая функция была квадратично интегрируемой функцией. В частности, в задачах с нормированной волновой функцией квадрат модуля волновой функции должен стремиться к нулю на бесконечности.

2.Условие однозначности волновой функции. Волновая функция должна быть однозначной функцией координат и времени, так как плотность вероятности обнаружения частицы должна определяться в каждой задаче однозначно. В задачах с использованием цилиндрической или сферической системы координат условие однозначности приводит к периодичности волновых функций по угловым переменным.

3.Условие непрерывности волновой функции. В любой момент времени волновая функция должна быть непрерывной функцией пространственных координат. Кроме того, непрерывными должны быть

также частные производные волновой функции , , . Эти частные производные функций лишь в редких случаях задач с идеализированными силовыми полями могут терпеть разрыв в тех точках пространства, где потенциальная энергия, описывающая силовое поле, в котором движется частица, испытывает разрыв второго рода.

Принцип суперпозиции квантовых состояний

Основная статья: Квантовая суперпозиция

Для волновых функций справедлив принцип суперпозиции, заключающийся в том, что если система может

пребывать в состояниях, описываемых волновыми функциями и , то она может пребывать и в состоянии, описываемом волновой функцией

при любых комплексных и .

Очевидно, что можно говорить и о суперпозиции (сложении) любого числа квантовых состояний, то есть о существовании квантового состояния системы, которое описывается волновой

функцией .

В таком состоянии квадрат модуля коэффициента 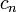определяет вероятность того, что при измерении система будет обнаружена в состоянии, описываемом волновой функцией .

Поэтому для нормированных волновых функций .

Операторы физических величин