
- •1.1. Определение волны. Механические и электромагнитные волны. Связь вида волн со свойствами среды и источника . Фронт волны. Понятие о скалярных и векторных волнах.
- •1.2. Монохроматические волны. Волновая поверхность, фазовая скорость. Длина волны, групповая скорость и ее физический смысл. Вектор Умова.
- •1.4 Волновое уравнение
- •2.1 «Поперечные бегущие волны, распространяющейся вдоль струны»
- •2.2 «Звуковые волны в газах»
- •3.1Вывод волнового уравнения для электромагнитного поля, фазовая скорость для электромагнитных волн
- •3.3 Поток энергии электромагнитной волны, вектор Пойнтинга
- •4.2 Явление интерференции, условие интерференции, перераспределение энергии, особенности интерференции в оптике
- •4.4. Примеры интерференции: двулучевая интерференция, интерференция при отражении от тонких пластинок, кольца Ньютона, многолучевая интерференция.
- •4.5. Дифракция света. Принцип Гюйгенса-Френеля.
- •2) Дифракция на круглом отверстии.
- •3)Дифракция на круглом экране(диске):
- •3. Опыт боте. Фотоэлектроны. Корпускулярно-волновой дуализм
- •3.Квантовая теория основные положения
- •6.Решение уравнения Шредингера для свободных микрочастиц с
- •6.Экспериментальное подтверждение гипотезы де Бройля. Опыт Дэвиссона и
- •7. «Частицы в бесконечной потенциальной яме. Квантовая энергия связанных частиц»
- •10.Атом водорода
3. Опыт боте. Фотоэлектроны. Корпускулярно-волновой дуализм





3.Квантовая теория основные положения
Тепловое излучение — электромагнитное излучение, испускаемое нагретыми телами за счет своей
внутренней энергии.
Абсолютно
черное тело —
тело,
поглощающее
всю энергию падающего на него излучения
любой частоты
при
произвольной температуре.
Энергия кванта излучения прямо пропорциональна частоте v излучения:
 где
h
= 6,6 • 10-34Дж
• с — постоянная Планка.
где
h
= 6,6 • 10-34Дж
• с — постоянная Планка.
Фотон — микрочастица, квант электромагнитного излучения.
Закон Стефана—Больцмана: Интегральная светимость абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры:
где σ = 5,67 • 10-8Вт/(м2 • К4) - постоянная Стефана—Больцмана.
Фотоэффект— явление вырывания электронов из твердых и жидких веществ под действием света.
Законы фотоэффекта
Фототок насыщения прямо пропорционален интенсивности света, падающего на катод.
Максимальная кинетическая энергия фотоэлектронов прямо пропорциональна частоте света и не зависит от его интенсивности.
Для каждого вещества существует минимальная частота света, называемая красной границей фотоэффекта, ниже которой фотоэффект невозможен.
Уравнение Эйнштейна для фотоэффекта:

Энергия фотона идет на совершение работы выхода и на сообщение вылетевшему фотоэлектрону кинетической энергии. Работа выхода— минимальная работа, которую нужно совершить для удаления электрона из металла.
Красная граница фотоэффекта
Корпускулярно-волновой дуализм — проявление в поведении одного и того же объекта как корпускулярных, так и волновых свойств. Корпускулярно-волновой дуализм — универсальное свойство любых материальных объектов.
Волновая теория правильно описывает свойства света при больших интенсивностях, т.е. когда число
фотонов велико.
Квантовая теория используется при описании свойств света при малых интенсивностях, т.е. когда число
фотонов мало.
Любой частице, обладающей импульсом р соответствует длина волны де Бройля:
В процессе измерения меняется состояние микрообъекта. Одновременное точное определение координаты и импульса частицы невозможно.
Соотношения неопределенностей Гейзенберга:
1. Произведение неопределенности координаты частицы на неопределенность ее импульса не меньше постоянной Планка:
2.
Произведение неопределенности энергии
частицы на неопределенность времени
ее измерения не меньше постоянной
Планка:
Постулаты Бора:

1. B устойчивом атоме электрон может двигаться лишь по особым, стационарным орбитам, не излучая при этом электромагнитной энергии
2.Излучение света атомом происходит при переходе атома из стационарного состояния с большей энергией
Ek в стационарное состояние с меньшей энергией Еn. Энергия излученного фотона равна разности энергий стационарных состояний:
Правило квантования орбит Бора:
На длине окружности каждой стационарной орбиты укладывается целое число n длин волн де Бройля,
Физический смысл волновой функции
В
координатном представлении волновая
функция
 зависит от координат (или обобщѐнных
координат) системы. Физический смысл
приписывается квадрату еѐ
зависит от координат (или обобщѐнных
координат) системы. Физический смысл
приписывается квадрату еѐ
модуля
 , который интерпретируется как плотностьвероятности
, который интерпретируется как плотностьвероятности
 (для дискретных спектров — просто
вероятность) обнаружить систему в
положении, описываемом координатами
(для дискретных спектров — просто
вероятность) обнаружить систему в
положении, описываемом координатами
 в момент времени
в момент времени :
:

.
Тогда в заданном квантовом состоянии системы, описываемом волновой
функцией
 , можно рассчитать вероятность
, можно рассчитать вероятность того, что частица будет обнаружена в
любой областиконфигурационного
пространства
конечного объема
того, что частица будет обнаружена в
любой областиконфигурационного
пространства
конечного объема


:  .
.
Следует также отметить, что возможно измерение и разницы фаз волновой функции, например, в опыте Ааронова — Бома.
Условия регулярности волновой функции
Вероятностный смысл волновой функции накладывает определенные ограничения, или условия, на волновые функции в задачах квантовой механики. Эти стандартные условия часто называют условиями
регулярности волновой функции.
1. Условие конечности волновой функции. Волновая функция не может принимать бесконечных
значений,
таких, что интеграл
 станет расходящимся. Следовательно,
это условие требует, чтобы волновая
функция была квадратично интегрируемой
функцией. В частности, в задачах с
нормированной волновой функцией квадрат
модуля волновой функции должен стремиться
к нулю на бесконечности.
станет расходящимся. Следовательно,
это условие требует, чтобы волновая
функция была квадратично интегрируемой
функцией. В частности, в задачах с
нормированной волновой функцией квадрат
модуля волновой функции должен стремиться
к нулю на бесконечности.
Условие однозначности волновой функции. Волновая функция должна быть однозначной функцией координат и времени, так как плотность вероятности обнаружения частицы должна определяться в каждой задаче однозначно. В задачах с использованием цилиндрической или сферической системы координат условие однозначности приводит к периодичности волновых функций по угловым переменным.
Условие непрерывности волновой функции. В любой момент времени волновая функция должна быть непрерывной функцией пространственных координат. Кроме того, непрерывными должны быть
также
частные производные волновой функции
 ,
, ,
, .
Эти частные производные функций лишь
в редких случаях задач с идеализированными
силовыми полями могут терпеть разрыв
в тех точках пространства, где потенциальная
энергия, описывающая силовое поле, в
котором движется частица, испытывает
разрыв второго рода.
.
Эти частные производные функций лишь
в редких случаях задач с идеализированными
силовыми полями могут терпеть разрыв
в тех точках пространства, где потенциальная
энергия, описывающая силовое поле, в
котором движется частица, испытывает
разрыв второго рода.
Принцип суперпозиции квантовых состояний

Для волновых функций справедлив принцип суперпозиции, заключающийся в том, что если система может
пребывать
в состояниях, описываемых волновыми
функциями
 и
и ,
то она может пребывать и в состоянии,
описываемом волновой функцией
,
то она может пребывать и в состоянии,
описываемом волновой функцией
 при
любых комплексных
при
любых комплексных
 и
и .
.
Очевидно, что можно говорить и о суперпозиции (сложении) любого числа квантовых состояний, то есть о существовании квантового состояния системы, которое описывается волновой
функцией
 .
.
В
таком состоянии квадрат модуля
коэффициента
 определяет вероятность того, что при
измерении система будет обнаружена в
состоянии, описываемом волновой функцией
определяет вероятность того, что при
измерении система будет обнаружена в
состоянии, описываемом волновой функцией .
.
Поэтому
для нормированных волновых функций
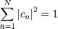 .
.


Операторы физических величин




5. Уравнение Шредингера. Стационарное уравнение Шредингера.
Отказавшись от описания движения частицы с помощью траекторий, получаемых из законов динамики, и определив вместо этого волновую функцию, необходимо ввести в
рассмотрение
уравнение, эквивалентное законам Ньютона
и дающее рецепт для нахождения
 в частных физических задачах. Таким
уравнением является уравнение Шрѐдингера.
в частных физических задачах. Таким
уравнением является уравнение Шрѐдингера.
Пусть волновая
функция задана в n-мерном
конфигурационном пространстве, тогда
в каждой точке с координатами
 ,
в определенный момент времениt
она будет иметь вид
,
в определенный момент времениt
она будет иметь вид
 .
В таком случае уравнение Шрѐдингера
запишется в виде:
.
В таком случае уравнение Шрѐдингера
запишется в виде:

где
 ,
, — постоянная Планка;
— постоянная Планка; — масса частицы,
— масса частицы,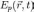 — внешняя по отношению к частице
потенциальная энергия в точке
— внешняя по отношению к частице
потенциальная энергия в точке в момент времени
в момент времени ,
, — оператор Лапласа (или лапласиан),
эквивалентен квадрату оператора набла
и вn-мерной
системе координат имеет вид:
— оператор Лапласа (или лапласиан),
эквивалентен квадрату оператора набла
и вn-мерной
системе координат имеет вид:

Стационарное уравнение Шрѐдингера
Форма уравнения
Шрѐдингера показывает, что относительно
времени его решение должно быть простым,
поскольку время входит в это уравнение
лишь через первую производную в правой
части. Действительно, частное решение
для специального случая, когда
 не является функцией времени, можно
записать в виде:
не является функцией времени, можно
записать в виде:

где функция
 должна удовлетворять уравнению:
должна удовлетворять уравнению:
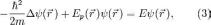
которое
получается из уравнения Шрѐдингера (1)
при подстановке в него указанной выше
формулы для
 (2).
Заметим,
что
это уравнение вообще не содержит времени;
в
связи с
этим оно называется стационарным
уравнением Шрёдингера (уравнение
Шрёдингера, не содержащее времени).
(2).
Заметим,
что
это уравнение вообще не содержит времени;
в
связи с
этим оно называется стационарным
уравнением Шрёдингера (уравнение
Шрёдингера, не содержащее времени).
