
Неопределенный интеграл. Основные понятия.
Первообразная
и неопределенный интеграл. Основные
свойства неопределенного интеграла.
Линейные свойства. Инвариантность
формулы интеграла. Таблица интегралов.
Вычисление интегралов, содержащих
квадратный трехчлен.
Интегрирование «по частям». Вычисление
интегралов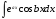 и
и

Замена переменной в неопределенном интеграле (подстановка). Интегрирование элементарных дробей.
Способы замены переменной
в неопределенном интеграле. Интегралы
вида
 .
Рациональная дробь. Элементарные дроби
типа,
I
типа,
III
типа,
V
типа. Интегрирование
элементарных дробей.
.
Рациональная дробь. Элементарные дроби
типа,
I
типа,
III
типа,
V
типа. Интегрирование
элементарных дробей.
Разложение рациональной дроби на элементарные. Интегрирование рациональных дробей.
Вычисление
интегралов вида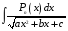 .
Определение коэффициентов разложения
(на примерах). Вычисление
интегралов вида
.
Определение коэффициентов разложения
(на примерах). Вычисление
интегралов вида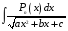 .
.
Геометрические приложения определенного интеграла. Несобственные интегралы.
Площадь плоской фигуры в прямоугольных и полярных координатах.
Площадь в прямоугольных координатах.
а) Пусть
криволинейная трапеция ограничена
двумя прямыми
 и
и
 осью
осью
 и
графиком непрерывной на
и
графиком непрерывной на
 функции
функции
 ,
которая
сохраняет знак на отрезке
,
которая
сохраняет знак на отрезке ).
).
Тогда площадь этой криволинейной трапеции определяется формулой:
 .
.
б) Если
функция задана в параметрической форме

(
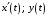 непрерывные
на отрезке
непрерывные
на отрезке
 функции),
то площадь криволинейной трапеции
определяется формулой:
функции),
то площадь криволинейной трапеции
определяется формулой:
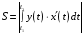 ,
где
,
где
 и
и
 определяются
соответственно из уравнений
определяются
соответственно из уравнений
 и
и
 и
(функции
и
(функции
 сохраняют
знак на отрезке
сохраняют
знак на отрезке
 ).
).
Замечание. Иногда площадь фигуры выражают в виде суммы или разности площадей участков, которые удовлетворяют указанным условиям.
Площадь в полярных координатах.
Пусть
криволинейный сектор ограничен дугой
кривой и
двумя полярными радиусами
и
двумя полярными радиусами
 и
и
 .
Пусть
.
Пусть непрерывна
на
непрерывна
на .
.
Тогда площадь криволинейного сектора выразится интегралом:
 .
.
Длина дуги в прямоугольных и полярных координатах.
Длина дуги в прямоугольных координатах.
а) Длина
дуги гладкой кривой
 ,
расположенной между двумя точками,
абсциссы которых равны
,
расположенной между двумя точками,
абсциссы которых равны
 и
и
 определяется формулой:
определяется формулой:
 .
.
б) Если
функция задана в параметрической
форме
 (
( и
и
 непрерывно
дифференцируемые на отрезке
непрерывно
дифференцируемые на отрезке
 функции),
то длина дуги кривой между точками,
абсциссы которых равны
функции),
то длина дуги кривой между точками,
абсциссы которых равны
 и
и
 определяется
формулой:
определяется
формулой:
 .
.
Длина дуги кривой в полярных координатах.
Пусть дуга
гладкой кривой задана в полярных
координатах уравнением от
от
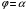 до
до
 .
Пусть
.
Пусть непрерывно
дифференцируема на
непрерывно
дифференцируема на .
.
Тогда длина дуги кривой выразится интегралом:
 .
.
Вычисление объема тела по площадям поперечных сечений.
Пусть дано
тело, у которого площадь
 любого
сечения, перпендикулярного оси, которую
принимают за ось
любого
сечения, перпендикулярного оси, которую
принимают за ось
 ,
является непрерывной функцией от
,
является непрерывной функцией от

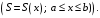
Тогда объем этого тела вычисляется по формуле:

Объем тела вращения.
Объем тела,
образованного вращением вокруг оси
 криволинейной трапеции, ограниченной
двумя прямыми
криволинейной трапеции, ограниченной
двумя прямыми
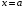 и
и
 ,
осью
,
осью
 и
графиком непрерывной на
и
графиком непрерывной на
 функции
функции
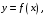 вычисляется по формуле:
вычисляется по формуле:

Площадь поверхности вращения.
Площадь
поверхности, образованной вращением
дуги гладкой кривой

 вокруг
оси
вокруг
оси
 ,
вычисляется по формуле:
,
вычисляется по формуле:

Несобственный
интеграл с бесконечным верхним
пределом.
Определение. Пусть
функция
 непрерывна
на интервале
непрерывна
на интервале
 .
Несобственным интегралом с бесконечным
верхним пределом называется предел
интеграла с переменным верхним пределом
(см. (1семестр) 15.6. 1.)), если
последний стремится к положительной
бесконечности:
.
Несобственным интегралом с бесконечным
верхним пределом называется предел
интеграла с переменным верхним пределом
(см. (1семестр) 15.6. 1.)), если
последний стремится к положительной
бесконечности:
 .
Допускается такая запись:
.
Допускается такая запись:

Если этот
предел конечный, то несобственный
интеграл сходится. Если этот предел
бесконечный или не существует, то
несобственный интеграл расходится.
Формула
Ньютона-Лейбница для сходящегося
несобственного интеграла бесконечным
верхним пределом.
Доказательство. где
где
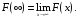 Сходимость
интеграла
Сходимость
интеграла


Несобственный
интеграл с бесконечным нижним
пределом.
Определение. Пусть
функция
 непрерывна
на интервале
непрерывна
на интервале
 .
.
Несобственным
интегралом с бесконечным нижним пределом
называется предел интеграла с переменным
нижним пределом, если последний стремится
к отрицательной бесконечности:
 .
(Возможен такой подход:
.
(Возможен такой подход:
 )
Несобственный интеграл
с двумя бесконечными пределами.
Определение.
Пусть функция
)
Несобственный интеграл
с двумя бесконечными пределами.
Определение.
Пусть функция
 непрерывна
на интервале
непрерывна
на интервале
 .
.
Несобственным
интегралом с двумя бесконечными
пределами называется сумма несобственных
интегралов:
 где
где
 любое
число.
Главное значение
несобственного интеграла.
Определение.
Главным значением
любое
число.
Главное значение
несобственного интеграла.
Определение.
Главным значением называется:
называется:
 .
Если этот предел существует, то он
называется главным значением, а интеграл
называется сходящим в смысле главного
значения.
.
Если этот предел существует, то он
называется главным значением, а интеграл
называется сходящим в смысле главного
значения.
Замечание.
Существуют расходящиеся интегралы,
которые сходятся в смысле главного
значения.
Геометрический
смысл сходящихся несобственных
интегралов.
Пусть функция
 непрерывна
на интервале а)
непрерывна
на интервале а)
 ;
б)
;
б)
 ;
в)
;
в)
 ,
тогда несобственный интеграл (если он
сходится) равен пределу площади
криволинейной трапеции с переменной
а) правой границей, б) левой границей,
в) обеими границами, которые стремятся
к бесконечности.
,
тогда несобственный интеграл (если он
сходится) равен пределу площади
криволинейной трапеции с переменной
а) правой границей, б) левой границей,
в) обеими границами, которые стремятся
к бесконечности.
Интегралы от разрывных функций. Интегралы, зависящие от параметра. Двойные интегралы.
Интегралы
от разрывных функций.
2.1.
1.Определение. Пусть функция
 имеет
на
имеет
на
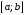 разрывы
1-го рода (устранимые и неустранимые)
(см. 6.2.2.1, 1семестр) в точках
разрывы
1-го рода (устранимые и неустранимые)
(см. 6.2.2.1, 1семестр) в точках
 ,
тогда
,
тогда
 .
.
Замечание.
Если в точке
 функция
не определена, ее доопределяют как
односторонний предел.
функция
не определена, ее доопределяют как
односторонний предел.
2.1. 2.
Определение. Пусть функция
 непрерывна
на
непрерывна
на
 и в точке
и в точке
 имеет
бесконечный разрыв. Несобственным
интегралом
имеет
бесконечный разрыв. Несобственным
интегралом
 называется предел интеграла с переменным
верхним пределом:
называется предел интеграла с переменным
верхним пределом:
 .
.
Интеграл сходится, если предел конечный.
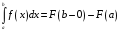 ,
где
,
где
 .
.
Пример.
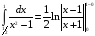 расходится,
так как
расходится,
так как
 .
.
2. 1. 3.
Определение. Пусть функция
 непрерывна
на
непрерывна
на
 и в точке
и в точке
 имеет бесконечный разрыв. Несобственным
интегралом
имеет бесконечный разрыв. Несобственным
интегралом
 называется предел интеграла с переменным
нижним пределом:
называется предел интеграла с переменным
нижним пределом:
 .
.
Интеграл сходится, если предел конечный.
 ,
где
,
где
 .
.
2.1. 4.
Определение. Пусть функция
 непрерывна
на
непрерывна
на
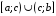 и в точке
и в точке
 имеет бесконечный разрыв.
Несобственным интегралом
имеет бесконечный разрыв.
Несобственным интегралом
 называется сумма несобственных
интегралов:
называется сумма несобственных
интегралов:
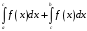 .
Интеграл сходится, если оба слагаемых
сходятся.
Интегралы,
зависящие от параметра.
2.2.1.
Определение. Пусть
функция
.
Интеграл сходится, если оба слагаемых
сходятся.
Интегралы,
зависящие от параметра.
2.2.1.
Определение. Пусть
функция
 определена
в прямоугольнике
определена
в прямоугольнике
Пусть
при каждом закрепленном
 из [c,d]
существует
из [c,d]
существует

Каждому
значению
 из [c,d]
будет отвечать свое, вполне определенное
зна-
из [c,d]
будет отвечать свое, вполне определенное
зна-
чение
этого интеграла. Следовательно представляет функцию переменной
представляет функцию переменной
 .
.
Введем
обозначение .
.
2.Случай,
когда пределы также зависят от параметра:
 .
Определение
и геометрический смысл двойного
интеграла.
Определение.
.
Определение
и геометрический смысл двойного
интеграла.
Определение.
Пусть
ограниченная функция
 задана в замкнутой ограниченной
области
задана в замкнутой ограниченной
области .
(См. 10.2.(ЭТАФ)) Разобьем эту область
на
.
(См. 10.2.(ЭТАФ)) Разобьем эту область
на
 частичных (непересекающихся)
областей с площадями
частичных (непересекающихся)
областей с площадями
 ,
где
,
где
 ,
возьмем в каждой частичной области
точку
,
возьмем в каждой частичной области
точку
 и составим интегральную сумму:
и составим интегральную сумму:

Обозначим
через
 наибольший диаметр частичных областей.
Двойным
интегралом
наибольший диаметр частичных областей.
Двойным
интегралом
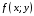 по области
по области
 называется
предел последовательности интегральных
сумм, при условии, что
называется
предел последовательности интегральных
сумм, при условии, что
 ,
если этот предел не зависит от способа
разбиения и выбора точек
,
если этот предел не зависит от способа
разбиения и выбора точек
 :
:
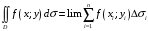
Геометрический смысл двойного интеграла.
2.3.2. 1.Определение. Цилиндрическим телом называется тело, ограниченное
а) замкнутой
областью
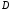 в
плоскости
в
плоскости ;
б) поверхностью
;
б) поверхностью
 где
функция
где
функция
 непрерывна и неотрицательна в
области
непрерывна и неотрицательна в
области
 ;
в) цилиндрической поверхностью,
у которой образующая параллельна оси
;
в) цилиндрической поверхностью,
у которой образующая параллельна оси
 ,
а направляющая является границей области
,
а направляющая является границей области
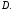
2.3.2. 2. Объем цилиндрического тела равен двойному интегралу:
2.3.2.3. Если
подынтегральная функция равна 1, то
двойной интеграл равен площади области
 :
:
 Свойства
двойного интеграла.
2.3.3.1.
Линейное свойство.
Свойства
двойного интеграла.
2.3.3.1.
Линейное свойство.

2.3.3.2. Если
область интегрирования
 разбита
на две области
разбита
на две области
 и
и без
общих внутренних точек
без
общих внутренних точек
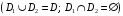 ,
то
,
то
 .
2.3.3.3.
Если во всех точках области
интегрирования
.
2.3.3.3.
Если во всех точках области
интегрирования
 функции
функции
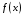 и
и удовлетворяют условию
удовлетворяют условию ,
то
,
то
Следствие. Если подынтегральная функция во всей области интегрирования не меняет знака, то двойной интеграл имеет тот же знак, что и функция.
2.3.3. 4.
Оценка двойного интеграла. Пусть
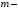 наименьшее
значение функции,
наименьшее
значение функции,
 наибольшее
значение непрерывной функции
наибольшее
значение непрерывной функции
 в области
в области
 ,
и пусть
,
и пусть
 площадь
области, тогда:
площадь
области, тогда: .
.
2.3.3.5.
Теорема о среднем (в двойном интеграле).
(Без доказательства) Если функция
 непрерывна в области
непрерывна в области
 ,
то существует точка
,
то существует точка
 ,
что
,
что
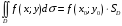 ,
где
,
где
 площадь
области
площадь
области
 .
Вычисление
двойного интеграла в декартовой системе
координат.
2.3.4.1. Определение.
Область
.
Вычисление
двойного интеграла в декартовой системе
координат.
2.3.4.1. Определение.
Область
 называется
правильной в направлении оси
называется
правильной в направлении оси
 ,
если она ограничена прямыми
,
если она ограничена прямыми
 и
и
 и кривыми
и кривыми
 ,
,
 (обе
функции непрерывны на отрезке
(обе
функции непрерывны на отрезке
 ,
и
,
и
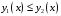 на
нем). (Любая прямая, параллельная оси
на
нем). (Любая прямая, параллельная оси
 пересекает
невертикальную границу области не
более, чем в двух точках.)
пересекает
невертикальную границу области не
более, чем в двух точках.)
2.3.4.2.
Определение. Область
 называется
правильной в направлении оси
называется
правильной в направлении оси
 ,
если она ограничена прямыми
,
если она ограничена прямыми
 и
и
 и кривыми
и кривыми
 ,
,
 (обе
функции непрерывны на отрезке
(обе
функции непрерывны на отрезке
 ,
и
,
и
 на
нем). (Любая прямая, параллельная оси
на
нем). (Любая прямая, параллельная оси
 пересекает
негоризонтальную границу области не
более, чем в двух точках.) (Самостоятельно
сделать схематический рисунок.)
пересекает
негоризонтальную границу области не
более, чем в двух точках.) (Самостоятельно
сделать схематический рисунок.)
2.3.4.3.
Теорема.
1) Пусть область
 является областью, правильной в
направлении оси
является областью, правильной в
направлении оси
 2)
2)
 3)
функция
3)
функция
 непрерывна
в области
непрерывна
в области
 4)
4)

Тогда
 (Без доказательства)
(Без доказательства)
2.3.4. 4.
Теорема
1) Пусть область
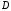 является областью, правильной в
направлении оси
является областью, правильной в
направлении оси
 2)
2) 3)
функция
3)
функция
 непрерывна
в области
непрерывна
в области
 4)
4)

Тогда

Вычисление
двойного интеграла в полярных
координатах.
Рассмотрим в
плоскости полярную систему координат
(см. 1.5. ан.геом.1семестр). Координатными
линиями будут линии
 и
и
 .
Первые представляют собой окружности
с центром в полюсе, а вторые- полупрямые
с началом в полюсе.
.
Первые представляют собой окружности
с центром в полюсе, а вторые- полупрямые
с началом в полюсе.
Частичная
область в полярных координатах
представляет криволинейный четырехугольник,
ограниченный полупрямыми
 и
и
 , а также дугами
, а также дугами
 и
и
 .
.
Тогда 

Так как второе слагаемое бесконечно малая более высокого порядка, чем первое, то
формула
для элемента площади:
 .
.
Поэтому
 ;
;
 .
.
Замечание .
1) Если полюс
не содержится внутри области интегрирования
 и
линии
и
линии пересекают
ее границу не более, чем в двух точках,
тогда
пересекают
ее границу не более, чем в двух точках,
тогда .
2) Если полюс содержится внутри области
интегрирования
.
2) Если полюс содержится внутри области
интегрирования
 и
линии
и
линии пересекают
ее границу в одной точке, тогда
пересекают
ее границу в одной точке, тогда
 Интеграл
Эйлера-Пуассона.
Интеграл
Эйлера-Пуассона.
 .
.
Замена переменных в двойном интеграле. Тройной интеграл.
Замена
переменных в двойном интеграле.
Формула
перехода: ,
где
,
где
 и
и
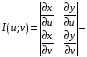 функциональный
определитель Якоби («якобиан»).
Определение
и
свойства тройного интеграла.
Определение.
Пусть функция
функциональный
определитель Якоби («якобиан»).
Определение
и
свойства тройного интеграла.
Определение.
Пусть функция
 трех
переменных
задана в
замкнутой ограниченной области
трех
переменных
задана в
замкнутой ограниченной области
 трехмерного
пространства.
Разобьем эту область сетью поверхностей
на конечное число (
трехмерного
пространства.
Разобьем эту область сетью поверхностей
на конечное число ( )
частичных (непересекающихся) областей
пространства с объемами
)
частичных (непересекающихся) областей
пространства с объемами
 где
где .
В каждой частичной области разбиения
возьмем произвольную точку
.
В каждой частичной области разбиения
возьмем произвольную точку
 и составим интегральную сумму:
и составим интегральную сумму:

Обозначим
через
 наибольший диаметр частичных областей.
Тройным
интегралом от функции
наибольший диаметр частичных областей.
Тройным
интегралом от функции
 по области
по области
 называется предел последовательности
интегральных сумм, при условии, что
называется предел последовательности
интегральных сумм, при условии, что
 ,
если этот предел не зависит от способа
разбиения и выбора точек
,
если этот предел не зависит от способа
разбиения и выбора точек
 :
:
 .
Свойства тройного
интеграла
2.3.3.1. Линейное
свойство.
.
Свойства тройного
интеграла
2.3.3.1. Линейное
свойство.

2.3.3.2. Если
область интегрирования
 разбита
на две области
разбита
на две области
 и
и без
общих внутренних точек
без
общих внутренних точек
 ,
то
,
то
 .
2.3.3.3.
Если во всех точках области
интегрирования
.
2.3.3.3.
Если во всех точках области
интегрирования
 функции
функции
 и
и удовлетворяют условию
удовлетворяют условию ,
то
,
то
Следствие.
Если подынтегральная функция во
всей области интегрирования не
меняет знака, то двойной интеграл
имеет тот же знак, что и функция.
3.4.1.2.
4. Оценка тройного интеграла
(Доказать
самостоятельно).
Пусть
 наименьшее
значение
функции,
наименьшее
значение
функции,
 наибольшее
значение
непрерывной функции
наибольшее
значение
непрерывной функции
 в области
в области
 ,
и пусть
,
и пусть
 объем
этой области, тогда:
объем
этой области, тогда: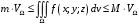 .
.
3.4.1.2.
5. Теорема
о среднем (для тройного интеграла) (Без
доказательства).
Если функция
 непрерывна в области
непрерывна в области
 ,
то существует точка
,
то существует точка
 ,
что
,
что
 .
.
3.4.1.2.
6. (
Доказать самостоятельно) Если
подынтегральная
функция равна 1,
то тройной
интеграл равен объему области
 :
:
 Вычисление
тройного интеграла в декартовых
координатах.
Пусть
область
Вычисление
тройного интеграла в декартовых
координатах.
Пусть
область
 ограничена сверху
и снизу
поверхностями:
ограничена сверху
и снизу
поверхностями:
 и
и
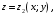 которые
проектируются
на плоскость
которые
проектируются
на плоскость
 в некоторую ограниченную область
в некоторую ограниченную область
 .
Кроме того, область
ограничена цилиндрической поверхностью,
образующие которой параллельны оси
.
Кроме того, область
ограничена цилиндрической поверхностью,
образующие которой параллельны оси
 .
Тогда
.
Тогда
 (без
доказательства)
(без
доказательства)
Если
область
 является
криволинейной трапецией правильной в
направлении оси
является
криволинейной трапецией правильной в
направлении оси
 (см.
2.3.4.1.)
(см.
2.3.4.1.)
то Замена
переменных в тройном интеграле.
Формула
перехода (без
доказательства):
Замена
переменных в тройном интеграле.
Формула
перехода (без
доказательства):
 ,
где
,
где
 и
и
 («якобиан»).
Тройной
интеграл в цилиндрических координатах.
(«якобиан»).
Тройной
интеграл в цилиндрических координатах.
Якобиан:
 .
.
Замечание.
Возможные значения для

Формула
перехода:

Тройной интеграл в сферических координатах. Криволинейный интеграл по плоским линиям .
Тройной
интеграл в сферических координатах.
Формула
перехода (см. 4.1.
1.) Криволинейный
интеграл первого рода по плоским линиям
(криволинейный интеграл по
длине).
Определение.
Пусть
в некоторой области
Криволинейный
интеграл первого рода по плоским линиям
(криволинейный интеграл по
длине).
Определение.
Пусть
в некоторой области
 задана
непрерывная функция двух переменных
задана
непрерывная функция двух переменных
 и
и
 гладкая
линия, целиком
расположенная в этой области. Разобьем
кривую
гладкая
линия, целиком
расположенная в этой области. Разобьем
кривую
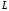 на
на
 участков. Пусть
участков. Пусть
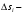 длина
дуги
длина
дуги
 го
участка кривой
го
участка кривой
 .
На каждом участке возьмем произвольную
точку
.
На каждом участке возьмем произвольную
точку
 и
построим интегральную сумму:
и
построим интегральную сумму: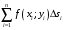
Криволинейным
интегралом первого рода (по длине) (по
линии
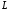 )
называется предел последовательности
интегральных сумм
)
называется предел последовательности
интегральных сумм
 при
условии, что наибольшая длина участка
разбиения стремится к нулю.
при
условии, что наибольшая длина участка
разбиения стремится к нулю.
 Свойства
криволинейных интегралов первого
рода.
4.2.2.3.
Свойства
криволинейных интегралов первого
рода.
4.2.2.3.
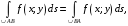 где
где
 и
и
 концы
линии
концы
линии
 .(Значение
криволинейного интеграла первого рода
не зависит от направления линии).
Криволинейный
интеграл второго
рода (по координатам)
по плоским линиям.
Определение.
Пусть в некоторой плоской области
.(Значение
криволинейного интеграла первого рода
не зависит от направления линии).
Криволинейный
интеграл второго
рода (по координатам)
по плоским линиям.
Определение.
Пусть в некоторой плоской области
 заданы непрерывные функции двух
переменных
заданы непрерывные функции двух
переменных
 и
и
 и
и
 гладкая
линия, целиком расположенная в этой
области. Разобьем кривую
гладкая
линия, целиком расположенная в этой
области. Разобьем кривую
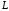 на
на
 элементарных участков:
элементарных участков:
 .
Проекции
.
Проекции
 того
участка на оси координат:
того
участка на оси координат:
 и
и .
Пусть на каждом участке произвольным
образом выбрана точка
.
Пусть на каждом участке произвольным
образом выбрана точка
 Составим интегральную сумму:
Составим интегральную сумму: .
.
Криволинейным
интегралом второго рода (по
координатам) (по линии
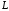 )
называется предел интегральной суммы
)
называется предел интегральной суммы
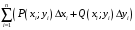 при условии, что наибольшая длина
участка разбиения стремится к нулю.
при условии, что наибольшая длина
участка разбиения стремится к нулю.
 Свойства
криволинейных интегралов второго
рода.
5.1. 2.4.
Свойства
криволинейных интегралов второго
рода.
5.1. 2.4.
 ,
где
,
где

