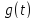Лекция, ЦОС, 30.09.2014

Лекция по ЦОС, 30.09.2014

Частотно-временное описание линейных непрерывных систем

Спектральное преобразование, которое мы использовали, можно приспособить к описанию линейных цепей.

Импульсной характеристикой (реакцией) g(t) линейной непрерывной системы называется ее отклик на единичный -импульс Дирака.

1

t

Известно, что любая линейная непрерывная система описывается во временной области импульсной характеристикой или комплексной частотной характеристикой , при этом любой сигнал на выходе линейной системы определяется как свертка этого сигнала с импульсной характеристикой.

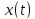
Ф

Из формулы (1.21) следует, что операция свертки имеет важное значение. Задавая различные импульсные характеристики, получаем на выходе по формуле (1.21) различные сигналы . Дальнейшую линейную систему, описываемую импульсной характеристикой, будем называть линейным непрерывным фильтром. Подбор такой оптимальной импульсной характеристики, при которой ошибка равна .

Переходной характеристикой фильтра 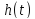называется ее отклик на единичное ступенчатое воздействие.

Очевидно, в соответствие с формулой (1.21) переходная характеристика будет равна:

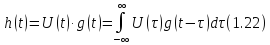
Комплексная частотная характеристика линейного фильтра определяется как преобразование Фурье от его импульсной характеристики.

Амплитудно-частотная характеристикой (АЧХ) линейного непрерывного фильтра будет равна:

Фазово-частотная характеристикой линейного непрерывного фильтра:

Пусть комплексная частотная характеристика фильтра известна, тогда спектр сигнала на его выходе описывается следующим выражением:

Полученная формула (1.26) непосредственно следует из свойства свертки (1.16). Спектр свертки равен произведению спектров.

Спектральная плотность мощности сигнала на выходе линейного фильтра равна:

, где – комплексно-сопряженное число.

Отсюда следует, что

Равенство Парсеваля для сигналов на выходе линейного фильтра в соответствии с формулой (1.16’):

Некоторые примеры комплексных спектров, СПМ и корреляционная функция

Линейный непрерывный фильтр называется физически реализуемым, если его импульсная характеристика имеет следующий вид:

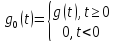
Фактически, условие физической реализуемости означает следующие требования:

Сигнал на выходе фильтра не может появиться раньше, чем он поступил на вход.

Так как будет линия задержки, кривая сместится вправо и будет выглядеть так: