12

Двойной интеграл. Задача об объеме цилиндрического тела.

z Рассмотрим тело, ограниченное

поверхностью z = f(x,y), цилиндрической

поверхностью с образующими,

параллельными оси oz и частью плоскости

f(P_i) xy (областью (D)). Такое тело называется

цилиндрическим (f(x,y) > 0).

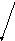у

x

∆σ_i P_i(ξ_i,η_i) (D)

Разобьем область (D) произвольным образом на n ячеек. Через границу каждой ячейки проведем цилиндрическую поверхность с образующими, параллельными оси oz и рассмотрим произведение f( P_i)∆σ_i = f(ξ_i , η_i)∙∆σ_i , где ∆σ_i - площадь ячейки.

Геометрически это произведение дает объем цилиндра основанием ∆σ_i и высотой f(P_i). Составим сумму

(*)

Эта сумма тем точнее характеризует истинный объем цилиндрического тела, чем меньше ∆σ_i. Поэтому за объем цилиндрического тела принимаем предел

(λ – наибольшая из хорд, стягивающих границы ячеек).

Если этот предел существует, если он не зависит от способа разбиения области (D) на частичные области и от выбора точек P_i, то он называется двойным интегралом от функции f(x,y) по области (D).

Очевидно,

Теорема существования.

Если функция f(x,y) непрерывна в области (D), то существует двойной интеграл от этой функции по области (D).

Вычисление двойного интеграла.

Вычислим , пользуясь тем, что Фиксируем x и проводим плоскость, перпендикулярную к оси ох.

Q(x) =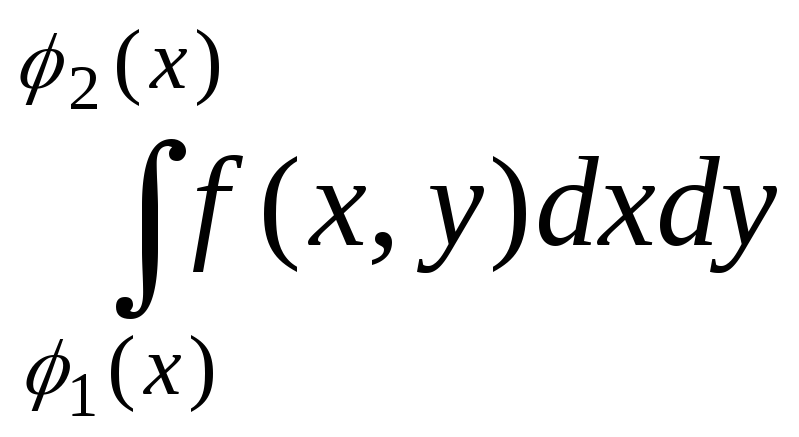. Тогда

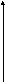
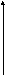
y y = φ₂(x) z z = f(x,y)

a x b x a y

y = φ₁(x) x

b

y = φ₂(x)

y = φ₁(x)

Пусть область (D) – правильная в направлении оси ox. Аналогично

y

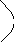
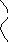
b

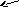
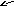x = φ₁(y) x = φ₂(y)

x

a

x

.

П р и м е р 1 . Вычислить где (D) область, ограниченная линиями y = x² и x = y². y y = x²

y x = y²

x = y²

y = x² y

y = x²

x

x x

x = y²

П р и м е р 2. Изменить порядок интегрирования

y

y = 2 2

y =

-4 x x 4 x

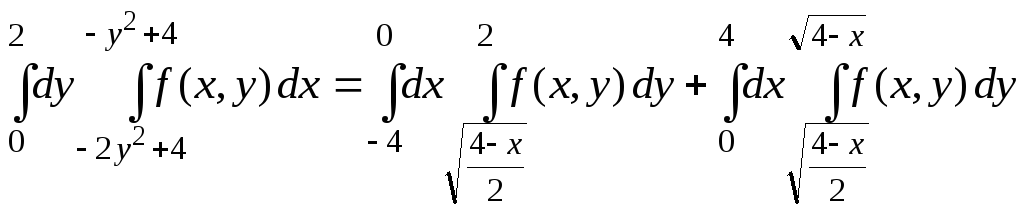
П р и м е р 3. Изменить порядок интегрирования.

5

1 y = x - 1

2 x 3

Свойства двойного интеграла.

1. Двойной интеграл суммы равен сумме двойных интегралов.

2. Постоянный множитель можно вынести за знак двойного интеграла.

3. Если область (D) разбита на две области (D₁) и (D₂) без общих внутренних точек, то

(D₁) (D₂)

П р и м е р . Свести двойной интеграл к двукратному.

(D): x = 2, y = x, xy = 1.

y

y = x 2

y = ¹/_{x x = y}

y x = 2

1 x 2 x 1

y x = 2

0.5 2 x

x = 1/y