Структура общего решения линейного однородного уравнения

Определение 5.Фундаментальной системойрешений линейного однородного дифференциального уравнения-го порядканазывается любая системалинейно независимых решений этого уравнения.

Теорема 3 (структура общего решения линейного однородного уравнения).Пусть функцииобразуют фундаментальную систему решений линейного однородного дифференциального уравнения-го порядка. Тогда функция

, (8)

где произвольные постоянные, является общим решением этого уравнения.

▲ Нужно проверить, что (8) удовлетворяет определению общего решения 7. При любых значениях постоянных ,эта функция, согласно свойству 3. решений линейного однородного дифференциального уравнения, является решением уравнения.

Теперь проверим второе условие определения 7: зададим в точке произвольные начальные условия,, …,и покажем, что постоянныеможно подобрать так, чтобы функция (8) удовлетворяла этим начальным условиям. Имеем:

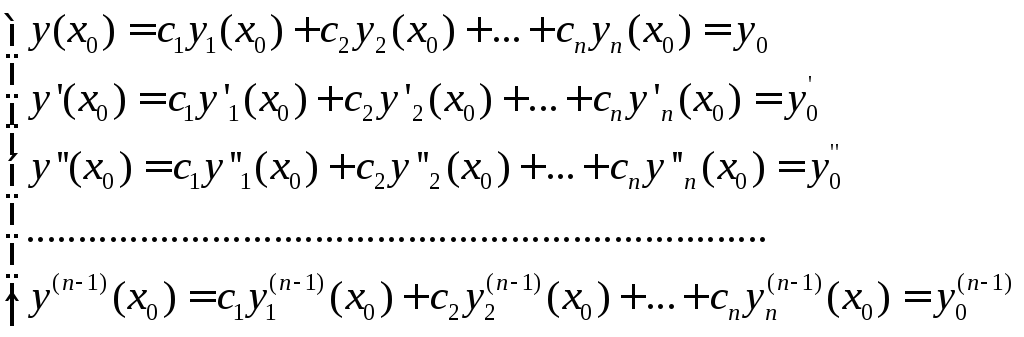. (9)

(9) является системой линейных уравнений снеизвестными. Определитель этой системы – это определитель, составленный из коэффициентов при неизвестных, т.е. определитель Вронского, который отличен от 0 в силу линейной независимости функций. Но тогда система (9), как системалинейных уравнений сnнеизвестными и определителем, не равным 0, имеет единственное решение. ■

Таким образом, для нахождения общего решения уравнения (1) нужно знать фундаментальную систему его решений. Однако в общем случае методов нахождения такой фундаментальной системы не существует.

Ниже будет описан способ нахождения фундаментальной системы решений для одного класса уравнений вида .

Линейные однородные уравнения с постоянными коэффициентами

В этом параграфе будет рассматриваться оператор вида

, (10)

где ,постоянные действительные числа, и уравнение вида,, или

. (11)

Уравнение (11) можно разделить на , поэтому к нему применимы предыдущие рассуждения, и общее решение (11) ищется по формуле (8):гдепроизвольные постоянные, афундаментальная система решений.

Для нахождения последней будем искать решения (11) в виде , гденекоторое число. Подставляяв (11) и учитывая, что, имеем:, или

. (12)

Т.е. функцияявляется решением уравнения (11) тогда и только тогда, когда числоявляется корнем уравнения (12).

Определение 6.Уравнение (12) называетсяхарактеристическим уравнениемдля дифференциального уравнения (11).

Характеристическое уравнение (12) получается из дифференциального уравнения (11) заменой производной на,(под нулевой производной функции понимается сама эта функция).

Определение 7.Левую часть характеристического уравнения (12) назовемхарактеристическим многочленоми обозначим.

Уравнение (12), как и всякое алгебраическое уравнение степени , имеет ровнокорней с учетом их кратности. Рассмотрим следующие 4 случая:

1. Все корни характеристического уравнения действительные и различные

Пусть эти корни. Этим корням соответствуютрешений уравнения (11):,, …,. Эти функции линейно независимы (см. пример выше), значит, они образуют фундаментальную систему решений уравнения (11), и общее решение этого уравнения задается формулой (8).

Пример. Решить дифференциальное уравнение .

Решение.

Характеристическое уравнение имеет вид: . Решаем это уравнение:Этим трем действительным различным корням соответствуют три решения из фундаментальной системы решений:, и общее рашение исходного уравнения имеет вид:.

2. Корни характеристического уравнения разные, но среди них есть комплексные

Так как в предыдущих рассуждениях нигде не использовалось, что корни характеристического уравнения и коэффициенты в решениях видадействительные числа, то все результаты пункта 1. справедливы и в случае таких комплексных чисел, однако в фундаментальной системе решений часть функций окажется тогда комплекснозначной. Чтобы от таких функций перейти к функциям с действительными значениями, поступим следующим образом.

Пусть корень характеристического уравнения (12) кратности 1. Так как это уравнение с действительными коэффициентами, тотоже корень уравнения (12) кратности 1. Этим корням соответствуют следующие решения уравнения (11):

и

.

Так как любая линейная комбинация (даже с комплексными коэффициентами) решений линейного однородного уравнения тоже является решением этого уравнения, то решениями (11) будут и функции

и.

Покажем, что если в фундаментальной системе решений заменитьина такие их линейные комбинации, то система останется фундаментальной. Для этого, согласно определению фундаментальной системы решений 5, достаточно доказать, что функции новой системы будут линейно независимыми. Приравняем к 0 линейную комбинацию таких функций:

.

Тогда

.

Так как линейно независимы, то все коэффициенты их линейной комбинации, равной 0, будут равны 0, т.е.;;;…;. Складывая и вычитая два первых равенства, имееми,, что и требовалось доказать.

Так же можно поступить с любой другой парой комплексно сопряженных корней кратности 1 уравнения (12).

Пример. Решить дифференциальное уравнение .

Решение.

Запишем характеристическое уравнение: . Комплексные корни этого уравненияимеют кратность 1, и общее решение дифференциального уравнение пишется в виде

.

3. Среди корней характеристического уравнения есть действительные кратные

Пусть действительный корень характеристического уравнения (12) кратности. Согласно предыдущему, ему соответствует решение уравнения (11). Но чтобы сохранить количество решенийв фундаментальной системе, этому корню должно соответствоватьрешений.

Оказывается, что такими решениями будут функции

,,, …,.

1) Эти функции являются решениями уравнения (11).

Проверим это в случае , т.е. при,,,…,.

В этом случае характеристическое уравнение (12) имеет вид

, где, или

, где,

тогда соответствующее дифференциальное уравнение (11) имеет вид

,,

и, очевидно, что все наши функции удовлетворяют этому уравнению, так как все встречающиеся в нем производные этих функций равны 0.

Случай сводится к случаюпутем замены, гденовая неизвестная функция. Рассмотрение такой замены, однако, требует достаточно громоздких выкладок, которые мы здесь приводить не будем.

2) Теперь проверим, что полученные решения линейно независимы. Приравняем к 0 (тождественно на любом конечном или бесконечном промежутке) произвольную линейную комбинацию этих решений и докажем, что все коэффициенты этой линейной комбинации обязательно равны 0. Имеем:

(последний переход уже был разобран выше).

Так же можно поступить с любым другим действительным кратным корнем характеристического уравнения. Можно проверить, что вся полученная таким образом система решений будет линейно независимой.

Пример. Решить дифференциальное уравнение .

Решение.

Характеристическое уравнение имеет вид: . Решаем это уравнение:;;;,. В соответствии с изложенным выше, общее решение дифференциального уравнения имеет вид.

4. Среди корней характеристического уравнения есть комплексные кратные

Так как в рассуждениях пункта 3. не использовалась действительность корней характеристического уравнения и коэффициентов в решениях вида, то результаты 3. справедливы и в случае комплексных чисел, однако при этом часть функций в фундаментальной системе решений окажется комплекснозначными. Чтобы от них перейти к функциям с действительными значениями, поступим аналогично пункту 2. и получим новую фундаментальную систему решений:

и, .

Пример. Решить дифференциальное уравнение .

Решение.

Характеристическое уравнение имеет вид: , или. Корни этого уравнения:,. В соответствии с результатами пункта 4, общим решением дифференциального уравнения будет функция.

Подведем итог: Общее решение уравнения

имеет вид

,

где произвольные постоянные, афундаментальная система решений уравнения, которая ищется следующим образом:

составляем характеристическое уравнение

Это уравнение имеет ровно корней (с учетом кратности). Этим корням соответствуют следующиефункций в фундаментальной системе решений:

1. Каждому действительному корню кратности 1 соответствует решение.

2. Каждой паре комплексно сопряженных корней и, кратности 1 каждый, соответствуют два решенияи.

3. Каждому действительному корню кратностисоответствуютрешений,,, …,.

4. Каждой паре комплексно сопряженных корней икратностикаждый, соответствуетрешений,,,,…,,.