4.4. Дисперсия: способы ее расчета, виды дисперсии, правило сложения дисперсии.

Моменты распределения

Дисперсия обладает рядом математических свойств, позволяющих упростить ее расчет.

Первое свойство заключается в том, что если из всех вариант вычесть какое-то постоянное число, то дисперсия от этого не изменится. Оно позволяет рассчитывать дисперсию не по отклонениям вариант от средней (часто имеющей дробное значение), а по отклонениям от целого числа. Второе свойство позволяет все варианты разделить на какое-то постоянное число, например на значение интервала, и исчислить дисперсию уменьшенных вариант, а полученную величину умножить на квадрат этого числа.

, .

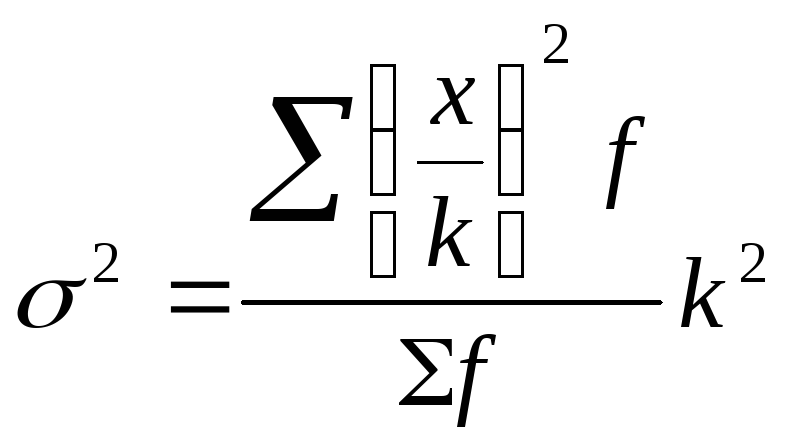где: ²_x – дисперсия отклонений вариантов от средней арифметической;

–дисперсия отклонений вариантов от произвольной величины А.

1. На этих свойствах основан расчет дисперсии способом отсчета от условного нуля или способ моментов, который заключается в нахождении вариант, уменьшенных на условно постоянную величину А и в k раз, где k – интервал, т.е. х₁=(х – А)/k, и последующем расчете дисперсии по формуле:

способ отсчета от условного нуля: ;

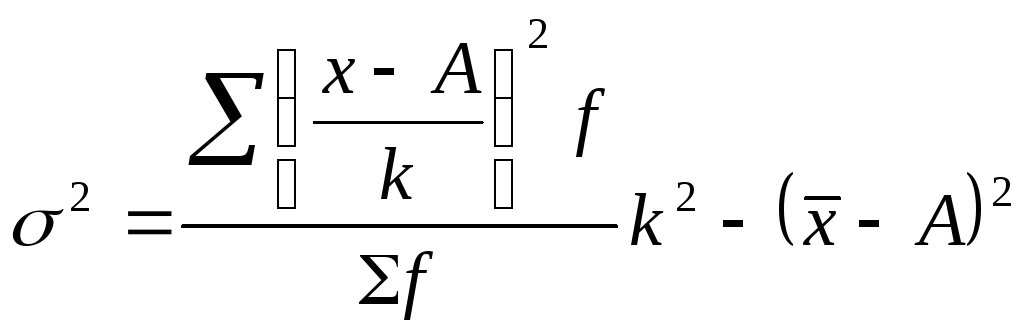способ моментов: , где

условный момент первого порядка: ;

условный момент второго порядка: ,

2. Дисперсия равна среднему квадрату значений признака за вычетом квадрата среднего значения признака:

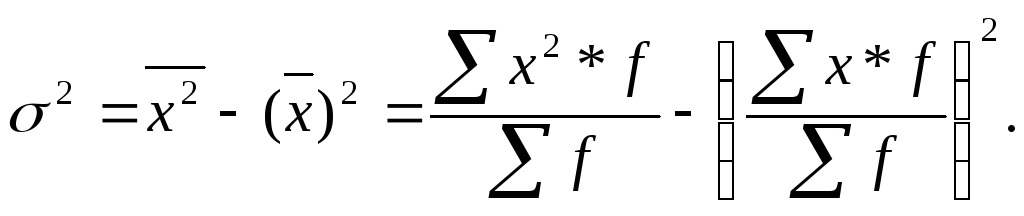
Расчеты дисперсии различными способами дают одинаковые результаты, что позволяет исследователю выбрать наиболее эффективный способ.

В ряде случаев изучают не среднюю величину признака, а долю единиц, обладающих тем или иным признаком. Например, доля междугородных телефонных соединений (разговоров), предоставленных с ожиданием до 1 часа. Это примеры альтернативных вариаций, когда имеются лишь два взаимоисключающих варианта: наличие или отсутствие признака у данной единицы совокупности (1 наличие признака, 0 отсутствие). В таких случаях определяется дисперсия альтернативного признака. Пусть доля единиц, обладающих данным признаком, равна р, а доля единиц, не обладающих этим признаком, 1–р, тогда

Естественно, средняя постоянная величины р есть сама эта величина, а дисперсия равна:

Средняя и дисперсия это частные случаи более широкого понятия обобщающих характеристик любого распределения моментов.

Момент распределения – это средняя арифметическая тех или иных степеней отклонений вариантов х от некоторой постоянной величины А:

_z = .

Порядок момента определяется величиной z, т.е. степенью, в которую возводится отклонение вариант. В зависимости от принятой величины А различают три вида моментов:

начальные (при А=0): ; центральные (при А=): ;

условные (при А≠0, А≠): .

Начальный момент первого порядка представляет собой среднюю арифметическую: ;

центральный момент второго порядка – дисперсию: . Центральный момент первого порядка ₁ всегда равен нулю (сумма отклонений вариант от средней равна нулю); центральный момент третьего порядка равен нулю в симметричном распределении.

Условные моменты самостоятельного значения не имеют, ими пользуются для упрощения вычисления центральных моментов: ₂ = m₂ – m²₁; ₃ = m₃ – 3m₁ m₂ + 2m³₁; ₄ = m₄ – 4m₃ m₁ + 6m₂ m²₁ – 3 m⁴₁.

Для исчисления условных моментов используется условная величина:

; ; ; ; где

В этом случае центральные моменты корректируются на величину k^z:

₂ = (m₂ – m₁²)k²; 3 = (m₃ – 3m₁ m₂ + 2m₁³)k³;

₄ = (m₄ – 4m₃ m₁ + 6m₂ m²₁ – 3 m⁴₁₎k⁴.

Наряду с изучением вариации признака по всей совокупности в целом часто возникает необходимость проследить количественные изменения признака по группам, на которые разбита вся совокупность, а также и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных дисперсий: общей, межгрупповой, внутригрупповой и средней из внутригрупповых дисперсий.

Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловливающих эту вариацию:

.

Межгрупповая дисперсия характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки:

, где

- соответственно средние и численности по отдельным группам,

- средняя всей совокупности.

Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основу группировки:

, где

- варианты групп, - численность группы,- средняя группы

Средняя из внутригрупповых дисперсий определяется по формуле:

.

Общая дисперсия определяется как сумма средней из внутригрупповых дисперсий и межгрупповой дисперсии:

.

Данная сумма называется правилом сложения дисперсий.

Согласно этому правилу общая дисперсия, возникающая под влиянием всех факторов, равна сумме дисперсий, возникающих под влиянием прочих факторов, и дисперсии, возникающей за счет группировочного признака.

На основании правила сложения дисперсий можно определить показатель тесноты связи между группировочным (факторным) и результирующим признаками. Он называется эмпирическим корреляционным отношением и рассчитывается как корень квадратный из отношения межгрупповой дисперсии к общей дисперсии:

.

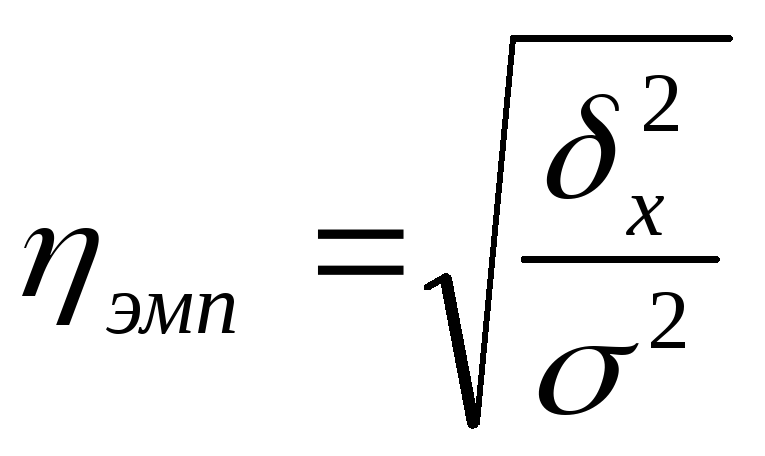Отношения межгрупповой дисперсии к общей дисперсии называется эмпирическим коэффициентом детерминации и показывает долю группировочного признака в общей вариации:

.