Правило Лопиталя (1661- 1704, Франция).
Пусть при нахождении предела имеем
неопределенность вида
Докажем это правило для неопределенности 0/0.
П р и м е р .
П р и м е р ы.
Сравнение быстроты роста функций.
1.
Вывод.
Логарифмическая функция растет
медленнее, чем любая степенная с
положительным показателем, а любая
степенная – медленнее, чем показательная
с основанием, большим единицы.
Функции многих переменных.
Изучение различных законов природы приводит к понятию функции многих переменных. Например, объем параллелепипедаV=xyz, т.е. является функцией трех переменных.
Определение. Переменная z называется функцией от переменных x и у, если каждой паре значений х и у по некоторому правилу или закону ставится в соответствие определенное значение z. z=f(x,y).
Уравнение z=f(x,y) определяет в пространстве поверхность, которая является графиком функции.Например, z = x2 + y2. Графиком является параболоид вращения.
С
овокупность
пар значенийх и у, в которых
функция имеет смысл, называютобластью
определения функции. Если каждую
пару (х,у) изображать точкой плоскостиOxy, то область определения
функцииz=f(x,y)
изобразится как некоторая совокупность
плоскости.Например
y
x
Функция f(x,y) называется непрерывной
в точке х = х0,у = у0,
если она определена в этой точке и
Частные производные.
f(x + ∆x,y)
–f(x,y)
= ∆xz– частное приращение функции по х.
Найдем
Аналогично определяется частная производная по у.
f(x,y+
-
частное приращение по у.
Полное приращение и полный дифференциал функции.
∆z=f(x+ ∆x,y+ ∆y) –f(x,y) – полное приращение
(x+ ∆x,y+ ∆y)
функции.
ρ
. (х, у)
х
Можно
показать, что полное приращение функции
отличается от полного дифференциала
на бесконечно малую высшего порядка,
чем ρ =
.
Повторное дифференцирование.
Рассмотрим функциюz=f(x,y).
Найдем
От этих производных можно также найти производные
Аналогично находятся производные более высоких порядков.
Например, z=x3– 4x2y+ 5y2,
Теорема.
Если
функция z
= f(x,
y) и ее
частные
производные f′x , f′y, f′′xy, f′′yx непрерывны в точке (х,у)
то 
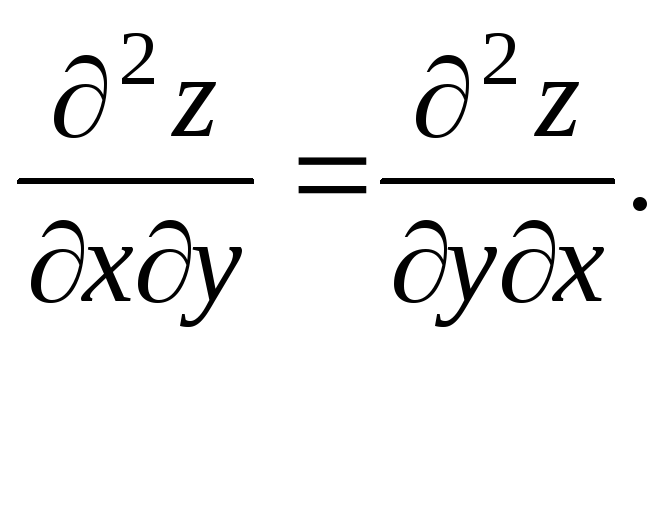
Из этой теоремы вытекает, что
