Геометрическая иллюстрация.

Свозрастаниемхtgα=f′(x) убывает, иf′′(x) < 0 .

С возрастанием х tgα=f′(х) возрастает, иf′′(x) > 0.

Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.

Необходимое условие точки перегиба. Если х = х₀ является абсциссой точкиперегиба, то f′′(х₀) либо равна нулю, либо не существует ( обращается в бесконечность)

Достаточное условие точки перегиба.

Если f ′′(x) при переходе через точку (x₀,f(x₀)) в направлении возрастания x меняет знак, то эта точка является точкой перегиба кривой y = f(x).

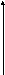
f(x₀)

x₀

x<x₀,f ′′(x) < 0, y = f(x) выпуклая.

x > x₀,f ′′(x) > 0, y = f(x) вогнутая.

Точка (x₀,f(x₀)) – точка перегиба.

Асимптоты кривой.

y y y

x x x

Асимптотой называется прямая, к которой кривая неограниченно приближается при удалении точки в бесконечность.

Наклонные асимптоты.

δ→ 0 при х→ ∞. Ищем уравнение асимптоты в видеy = kx + b.

δ = y_A –y_K = kx + b – f(x) →0 приx→∞. Отсюдаf(x) = kx + b – δ. Найдем

δ = kx + b – f(x) → 0, т.е.

Если хотя бы один из пределов kилиbне существует, то наклонных асимптот нет. Еслиk = 0, то имеем горизонтальную асимптоту.

Вертикальные асимптоты. Уравнение ищем в видеx = a,

Для рациональных функций – вертикальные асимптоты проходят в тех точках, которые обращают в нуль знаменатель.Пример.

Формула Тейлора (1685 − 1731, Англия).

Рассмотрим функцию f(x), имеющую в точкеx = a производные любого порядка. Возникает вопрос, нельзя ли эту функцию приближенно представить в виде многочлена по степенямx – a. Например, y= cos x.

y = 1

-3 3

√2 π /2

y = cos x

Построим многочлен P_n (x)такой, что

P_n(a) = f(a), P_n′(a) = f ′(a), ..., P_n⁽ⁿ⁾(a) = f ⁽ⁿ⁾(a) (*)

Пусть

P_n(x) = a₀ + a₁ (x – a) +a₂ (x - a)² + ...+ a_n (x – a)ⁿ. _.

Подберем коэффициенты этого многочлена так. чтобы удовлетворялись соотношения (*).

P_n′(x) = a₁ + 2a₂(x – a) +3a₃(x – a)² ... + n a_n(x – a)^{n – 1}, ,

P_n′′(x) = 2a₂ + 2∙3a₃ (x – a) + ... + n(n − 1) a_n (x – a)^{n – 2} ,

P_n′′′(x) = 2∙3a₃ + ... + n(n – 1)(n – 2) a_n(x – a)^{n – 3},

...........................................................................

P_n⁽ⁿ⁾(x) = n(n – 1)(n – 2)....(n – (n – 1))a_n,

P_n(a) = a₀ = f(a), a₀ = f(a),

P_n′(a) = a₁ = f ′(a), a₁ =

Обозначим f(x) – P_n(x) = R _n. Отсюда

f(x) = P_n(x) + R _nили

f(x) = +R _n(**)

Формула (**) называется формулой Тейлора. R _n–остаточный членформулы Тейлора. Можно показать, что

ξ – некоторое число между x и a.Остаточный член указывает на величину ошибки при замене функцииf(x)многочленомР_n (x).

Формула Тейлора переходит в бесконечный ряд Тейлора.

Если a = 0, то

П р и м е р ы .

1. y = e ^x. y′ = y′′ = .... = y⁽ⁿ⁾ = e^x.y(0) = y′(0) = y^′′(0) =.... = y⁽ⁿ⁾(0) = 1. Отсюда