
- •Определение производной
- •Производные тригонометрических функций.
- •Дифференциал функции.
- •Возрастание и убывание функции.
- •Геометрическая иллюстрация.
- •Экстремумы функции
- •Второе достаточное условие экстремума.
- •Выпуклость и вогнутость графика функции.
- •Достаточное условие выпуклости и вогнутости кривой.
- •Геометрическая иллюстрация.
- •Правило Лопиталя (1661- 1704, Франция).
- •Сравнение быстроты роста функций.
- •Функции многих переменных.
- •Полное приращение и полный дифференциал функции.
- •Повторное дифференцирование.
Дифференциал функции.
Дифференциалом аргумента называется его приращение dx = ∆x.
Дифференциалом функции называется произведение производной на приращение аргумента dy = f′(x)∙∆x или dy = f′(x)∙dx.
Замечание:
![]()
Сравнение дифференциала с приращением.
Пусть
![]()
![]()
![]() ∆y
и ∆xодного порядка
малости.
∆y
и ∆xодного порядка
малости.
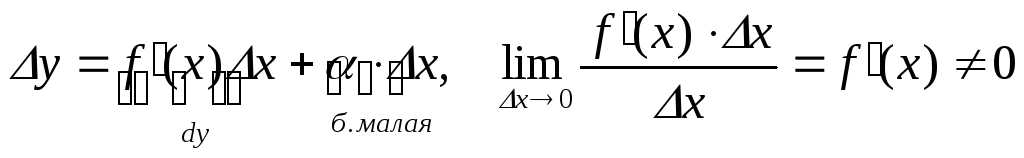 .dyи ∆xодного
порядка малости,
т. е.dyи ∆yодного порядка
малости.
.dyи ∆xодного
порядка малости,
т. е.dyи ∆yодного порядка
малости.
![]() α∙∆x– бесконечно малая
более высокого порядка малости, чем
∆x.
α∙∆x– бесконечно малая
более высокого порядка малости, чем
∆x.
![]() .Дифференциал есть главная часть
приращения функции.
.Дифференциал есть главная часть
приращения функции.
Дифференциал функции отличается от приращения функции на бесконечно малую
более высокого порядка, чем приращение аргумента.
Геометрический смысл дифференциала функции.
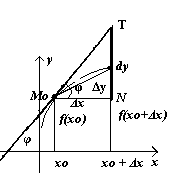 dy
=f′(x)∙∆x=tgφ∙∆x=NT.
dy
=f′(x)∙∆x=tgφ∙∆x=NT.
Дифференциал равен приращению ординаты касательной.
Свойства дифференциала.
Дифференциал суммы равен сумме дифференциалов.
d(u + v) = du + dv.
Дифференциал произведения d(u v) = du∙ v + u dv.
Дифференциал сложной функции.
y = f(u), u = φ(x), dy = y′x
dx =![]()
dy = f ′(u) du – инвариантность формы дифференциала.
Дифференциалы высших порядков.
dy = f
′(x)∙dx,
отсюда
![]()
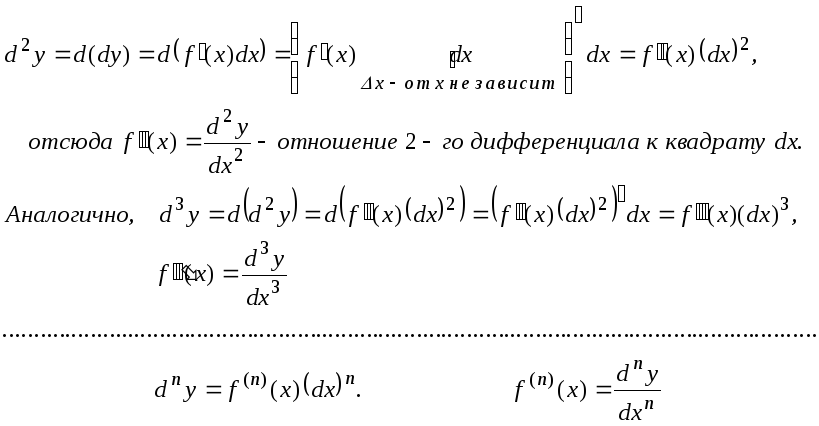
Гиперболические функции.
Во многих приложениях математического анализа встречаются комбинации показательных функций.
Определения.
![]()
Из определений гиперболических функций следуют соотношения:
ch2x–sh2x= 1,sh2x= 2shx∙chx,ch2x=ch2x+sh2x,sh(α±β) =shαchβ±chαshβ.Производные от гиперболических функций.
![]()
Теорема Ролля.
Если функция f(x) определена и непрерывна на замкнутом промежутке [a, b], имеет производную во всех внутренних точках этого промежутка и принимает на концах промежутка равные значения, то внутри промежутка найдется, по крайней мере, одна такая точка x = ξ, что f ′(ξ) = 0.
Геометрический смысл.
 y
y 

 f(a)
= f(b),
kкас= 0.
f(a)
= f(b),
kкас= 0.

 A C
A C B На
гладкой дуге [a,
b] найдется такая
точка
B На
гладкой дуге [a,
b] найдется такая
точка
 f(a) f(b) С,
в которой касательная параллельна
хорде.
f(a) f(b) С,
в которой касательная параллельна
хорде.
a ξ b x
Теорема Лагранжа (1736-1813, Франция).
Если функция определена и непрерывна на замкнутом промежутке [a,b] и имеет производную во всех внутренних точках этого промежутка, то внутри этого промежутка найдется, по крайней мере, одна такая точка х = ξ, что f(b) – f(a) = f′(ξ)∙(b – a).
Геометрический смысл теоремы Лагранжа.
И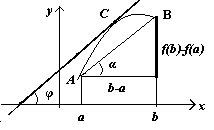 меем
гладкую дугу АВ.
меем
гладкую дугу АВ.
![]()
На гладкой дуге АВ найдется такая точка С, в которой касательная параллельна хорде АВ.
Доказательство. Рассмотрим функциюF(x) = f(x) – λx. Подберем λ так, чтобы выполнялись условия теоремы Ролля.
F(x) – определена и непрерывна на [a, b], т.к. определена и непрерывна функцияf(x),.
F′(x)= f ′(x) – λ − существует,
Подберем λ так, чтобы выполнялись условия F(a) = F(b), т.е.f(a) – λa = f(b) – λb,
![]()
По теореме Ролля найдется такая точка x =ξЄ (a, b), чтоF′(ξ) = 0, т.е.
Возрастание и убывание функции.
Функция называется возрастающей, если большему значению аргумента соответствует большее значение функции.
Функция называется убывающей, если большему значению аргумента соответствует меньшее значение функции.



 y y
y y

 f(x1)
f(x1)

 f(x1) f(x2)
f(x2)
f(x1) f(x2)
f(x2)
x1 x2 x x1 x2 x
x1 < x2, f(x1) < f(x2) x1 < x2, f(x1) > f(x2)
возрастающая функция, убывающая функция.
Признаки возрастания и убывания.
Если f′(x) > 0 для всех x, принадлежащих интервалу (a, b), то f(x) возрастает на этом интервале.
Если f′(x) < 0 всех x, принадлежащих интервалу (a, b), то f(x) убывает на этом интервале.
Доказательство.
![]() .
.
Причем x1<x2. По теореме Лагранжа имеемf(x2) –f(x1) =f′(ξ)(x2 – x1) > 0. Отсюдаf(x2) >f(x1) – функция возрастает на (a, b)
Аналогично для убывающей функции.
