19

Дифференциальное исчисление.

Понятие производной связано с понятиями скорости различных процессов.

Определение производной

Рассмотрим функцию f(x). ∆x– приращение аргумента, ∆у – приращение функции.

-

(справа и слева)

- производная функции f(x).

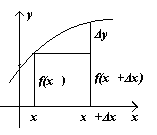
Обозначение производной:

Производной называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Дифференцирование – это нахождение производной.

Замечание: для существования производной необходимо, чтобы ,т.е. функция должна бытьнепрерывной.

Задача о касательной.

О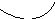пределение касательная есть предельное положение секущей, проведенной через две точки кривой при неограниченном сближении этих точек. М₁→ М₀, М₀М₁→ М₀Т.

T

М₁ М₁ .

М₁

Гладкая кривая Негладкая кривая.

(в каждой точке можно провести одну касательную)

В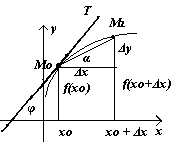ыясним геометрический смысл производной функцииy=f(x) в точке х = х_0.

Пусть М₁ → М₀, М₀М₁→М₀Т, tgα→tgφ,

Производная равна угловому коэффициенту касательной.

Основные правила дифференцирования.

1. Производная постоянной равна нулю. (с)′ = 0.

2. Производная суммы равна сумме производных (u + v)′ = u′ + v′.

3. Производная произведения (uv)′ = u′v + uv′. Следствия.

1.Постоянный множитель можно вынести за знак производной (сu)′ = cu′.

2. (uvw)′ = u′vw + uv′w + uvw′.

4. Производная частного

5. Производная степенной функции (xⁿ)′ =n∙x^n-1

П р и м е р ы. 1. y=x³,y′ = 3x².

2.

3. y = ¹/_x , y′ =

4. x′ = 1.

6. Производная сложной функции. y = f(u), u =φ(x), y– сложная функция х.y = f(φ(x)).Примеры.

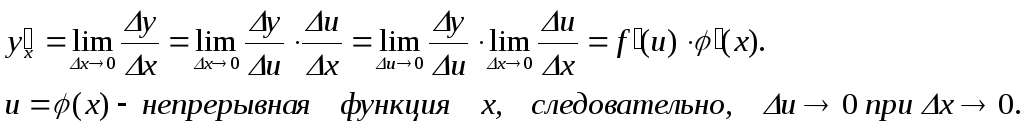
П р и м е р ы.

1. 

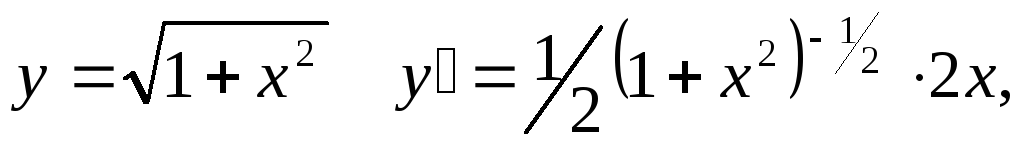
2. y = ¹/_3x+2, y′ = -1∙(3x + 2)^-2∙3.

Важные частные случаи (нужно помнить).

Производные тригонометрических функций.

1. y = sin x,

(sin x)′ = cos x

2. Аналогично (cos x)′ = -sin x.

3. 

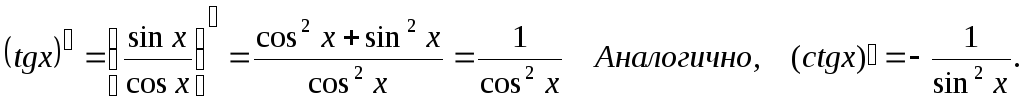
Производные логарифмических функций.

Производные неявных функций.

Определение: у есть неявная функция х, если уравнение, связывающее х и у, не решено относительно у.

F(x,y) = 0. (*)

П р и м е р .

1. x² + y² = 1,

2. sin(x + y) + xy = 0

Правило. Чтобы найти производную у′ от функции, заданной неявно, нужно почленно продифференцировать уравнение (*) по х, учитывая, что у есть функция от х. Полученное уравнение решить относительно у′.

1. 2х + 2у∙у′ = 0, y′ = -^x/_y .

2. cos(x + y) ∙(1 + y′) +y +xy′ = 0,

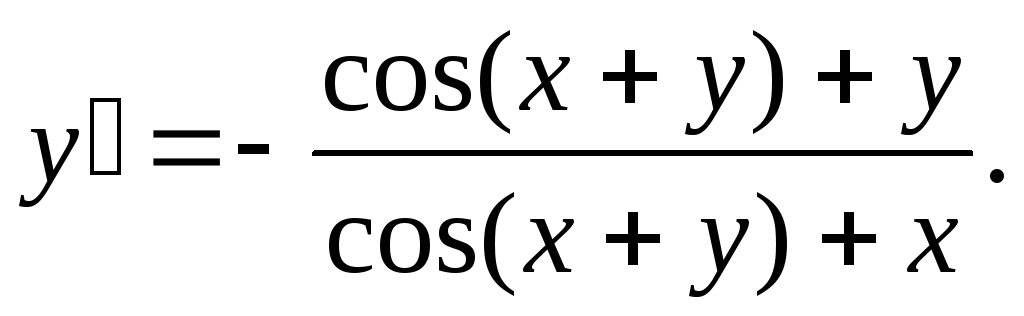
Производная показательной функции.

y=a^x,lny=x∙lna,¹/_yy′ =lna,y′ =a^x∙lna (a^x)′ = a^x∙lna (e^x)′ = e^x∙lna

Производная степенной функции

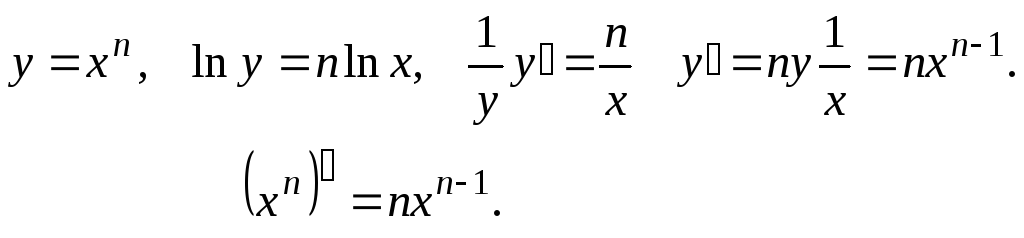
Логарифмическое дифференцирование.

y= (u(x))^v(x)П р и м е р .y = (x² + 1)^{cos x}, lny = cosx ln(x² + 1),

¹/_y y′ = −sin x∙ ln(x² + 1) + cos x∙ .

Производные обратных тригонометрических функций.

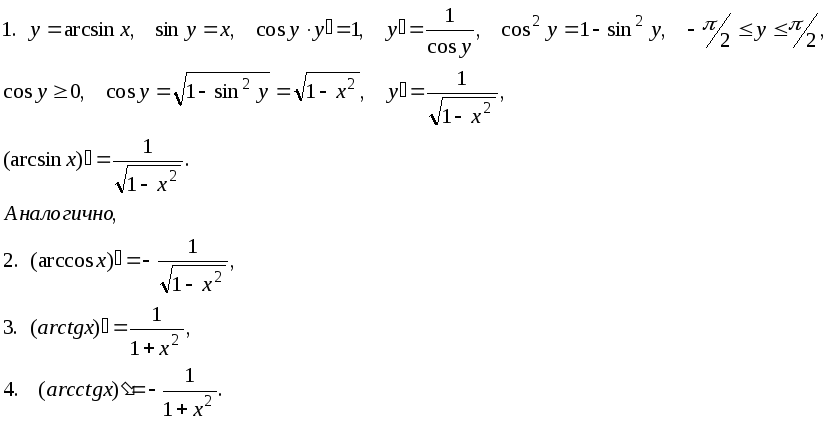
Производные высшего порядка.

y =f(x), y′ = f′(x), y′′ = f′′(x), y′′′ = f′′′(x), ….

2-я производная – это производная от первой производной и т.д.

Другие обозначения:

П р и м е р ы.

1. y = x⁴, y′ = 4x³, y′′ =12x², y′′′ =24x, y^1V =24, y^V = 0.

2. y = e^kx, y′ =ke^kx, y′′ =k²e^kx, y′′′ = k³e^kx, …. y⁽ⁿ⁾ = kⁿe^kx.

Параметрическое задание функций.

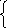
x = φ(t), Совместно эти уравнения определяют функцию или кривую, заданную

y=ψ(t) параметрически.y

Пр и м е р.

1. Окружность.x = a φ(t), x

y = a ψ(t). tt x

Точка М обегает окружность, если tпроходит интервал длиной 2π.

2. Эллипс. x=a φ(t), Если исключитьt, то получится каноническое уравнение

y = b ψ(t). эллипса. .

3. Циклоида. x = a(t – sin t), y = a(1 – cos t). 0

πa 2πа x

Производные функций, заданных параметрически.

x=φ(t),φ(t) и ψ(t) – непрерывны, следовательно, ∆xи ∆y→ 0 при ∆t→ 0,

y= ψ(t)t- промежуточная переменная.

y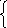′_x = y′_t∙ t′_x , y′_t = ψ′(t), 1 = φ′(t)∙t′_x, t′_x= ¹/_φ′(t).

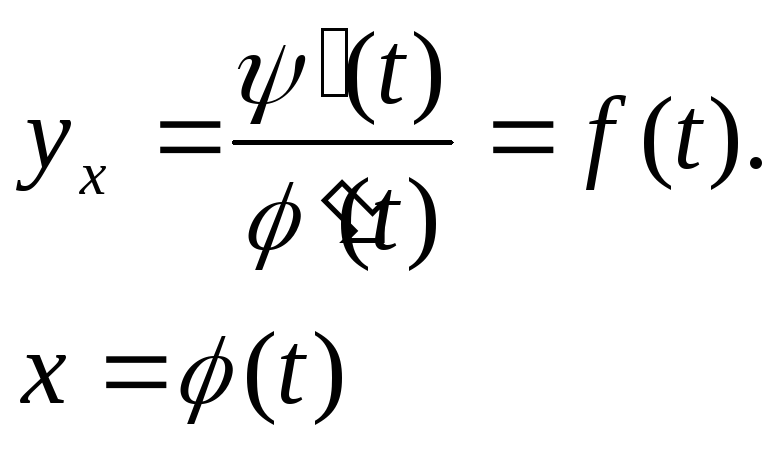
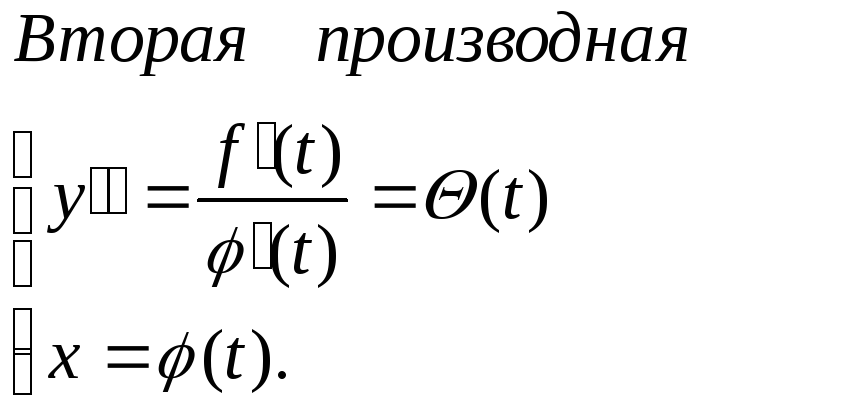
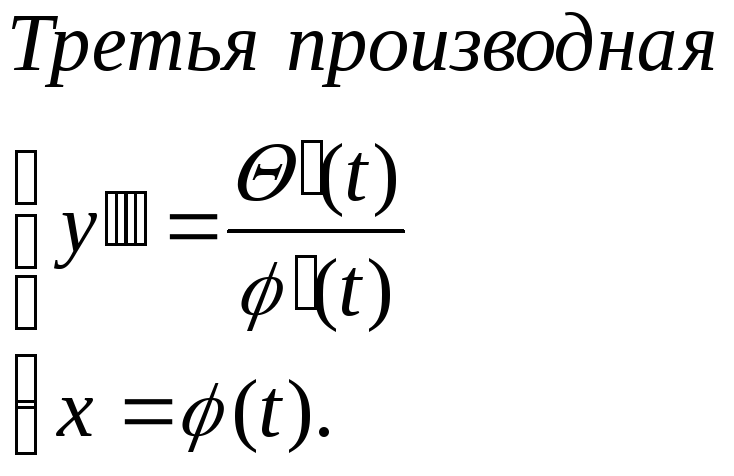П р и м е р .