ТЭЦ 12 вариант

ОСНОВЫ ТЕОРИИ ЦЕПЕЙ

Контрольная работа.

Вариант 12.

N0=2

N1=1

Задача 1.1. Линейный резистивный элемент имеет сопротивление R_Л = 1050 Ом.

Нелинейный резистивный элемент характеризуется вольт-амперной характеристикой вида

i = a₁ u + a₂ u² + a₃ u³, (0  u  10 В)

a₁ = 4,2 мА/В, а₂ = –0,35 мА/В² а₃ = –0,001 мА/В³

Рассчитайте вольт-амперную характеристику эквивалентного соединения нелинейного и линейного резистивных элементов при их параллельном и последовательном соединении.

Решение.

а) последовательное соединение

i

R_Л R_Н

U_Л U_Н

U

напряжение на соединении равно сумме напряжений на каждом резисторе, ток через соединение равен току через каждый резистор.

I, мА	0	3,849	6,992	9,423	11,136	12,125	12,384	11,907	10,688	8,721	6
Uн, В	0	1	2	3	4	5	6	7	8	9	10
Uл, В	0	4,041	7,342	9,894	11,693	12,731	13,003	12,502	11,222	9,157	6,3
U, В	0	5,04	9,34	12,89	15,69	17,73	19,00	19,50	19,22	18,16	16,3

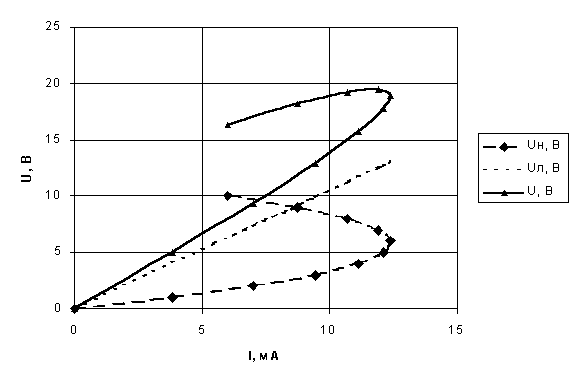
Рис. 1.1. Вольт-амперная характеристика эквивалентного соединения нелинейного и линейного резистивных элементов при их последовательном соединении.

б) параллельное соединение

i

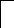i_Н i_Л

u

R_Н R_Л

ток на соединении равен сумме токов на каждом резисторе, напряжение на соединении равно напряжению на каждом резисторе.

U, В	0	1	2	3	4	5	6	7	8	9	10
Iн, мА	0	3,849	6,992	9,423	11,136	12,125	12,384	11,907	10,688	8,721	6
Iл, мА	0	0,952	1,905	2,857	3,810	4,762	5,714	6,667	7,619	8,571	9,524
I, мА	0	4,80	8,90	12,28	14,95	16,89	18,10	18,57	18,31	17,29	15,52

Рис. 1.2. Вольт-амперная характеристика эквивалентного соединения нелинейного и линейного резистивных элементов при их параллельном соединении.

Задача 1.2. На рисунке изображена электрическая схема.

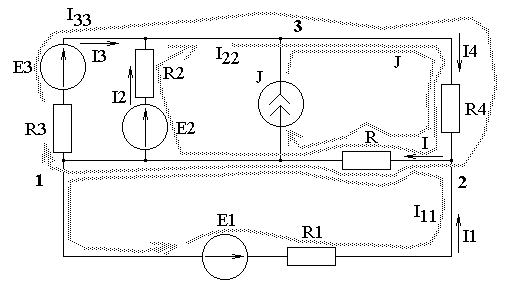
Рис. 2.1. Электрическая схема.

Параметры схемы заданы в таблице.

E1, В	E2, В	E3, В	J, А	R1, Ом	R2, Ом	R3, Ом	R4, Ом	R, Ом
18	28	32	2,3	30	25	40	60	20

Задание:

- определить токи во всех ветвях схемы методом контурных токов;

- определить токи во всех ветвях схемы методом узловых напряжений;

- результаты расчета токов, выполненного двумя методами, сравнить между собой;

- рассчитать значение тока в ветви с элементом R, используя метод эквивалентного генератора напряжения (тока);

- составить баланс мощностей.

Решение.

Выберем положительные направления токов, как указано на схеме рис. 2.1.

Число ветвей N_в=6, число узлов N_у=3, число источников тока N_T=1.

Число независимых уравнений по методу контурных токов:

K = N_в – N_у + 1 – N_Т = 6 – 3 + 1 – 1 = 3

Число независимых уравнений по методу узловых напряжений:

У= N_у – 1 = 3 – 1 = 2

Выбираем (рис.2.1) контуры и составляем для этих контуров уравнения:

I₁₁ (R₁ + R) + I₂₂ R + I₃₃ R + JR = E₁

I₂₂ (R₂ + R₄ + R) + I₁₁ R + I₃₃ (R₄ + R) + J (R₄ + R) = E₂

I₃₃ (R₃ + R₄ + R) + I₁₁ R + I₂₂ (R₄ + R) + J (R₄ + R) = E₃

50 I₁₁ + 20 I₂₂ + 20 I₃₃ + 46 = 18

20 I₁₁ + 105 I₂₂ + 80 I₃₃ + 184 = 28

20 I₁₁ + 80 I₂₂ + 120 I₃₃ + 184 = 32

25 I₂₂ – 40 I₃₃ = –4

I₂₂ = –0,16 + 1,6 I₃₃

50 I₁₁ + 20*(–0,16 + 1,6 I₃₃) + 20 I₃₃ + 46 = 18

50 I₁₁ + 52 I₃₃ = –24,8

I₁₁ = –0,496 – 1,04 I₃₃

20*(–0,496 – 1,04 I₃₃) + 80*(–0,16 + 1,6 I₃₃) + 120 I₃₃ + 184 = 32

227,2 I₃₃ = –129,28

I₃₃ = –0,569 А

I₁₁ = –0,496 – 1,04 I₃₃ = 0,096 А

I₂₂ = –0,16 + 1,6 I₃₃ = –1,07 А

I₁ = I₁₁ = 0,096 А

I₂ = I₂₂ = –1,07 А

I₃ = I₃₃ = –0,569 А

I₄ = J + I₂₂ + I₃₃ = 0,661 А

I_R = J + I₁₁ + I₂₂ + I₃₃ = 0,757 А

Определение токов методом узловых напряжений. Обозначаем узлы 1, 2, 3. Соединяем узел 1 с землей, тогда V₁=0. Тогда значения токов в ветвях можно записать как

I₁ = Y₁ (E₁ – V₂)

I₂ = Y₂ (E₂ – V₃)

I₃ = Y₃ (E₃ – V₃)

I₄ = Y₄ (V₃ – V₂)

I = Y V₂,

где

Y₁ = 1/R₁ = 0,0333

Y₂ = 1/R₂ = 0,04

Y₃ = 1/R₃ = 0,025

Y₄ = 1/R₄ = 0,0167

Y = 1/R = 0,05.

Запишем уравнения для узлов по первому закону Кирхгофа:

I = I₁ + I₄

I₂ + I₃ + J = I₄

Подставим узловые потенциалы:

Y V₂ = Y₁ (E₁ – V₂) + Y₄ (V₃ – V₂)

Y₂ (E₂ – V₃) + Y₃ (E₃ – V₃) + J = Y₄ (V₃ – V₂)

Приведем подобные слагаемые:

(Y+Y₁+Y₄) V₂ – Y₄V₃ = Y₁E₁

Y₄V₂ – (Y₂+Y₃+Y₄) V₃ = –Y₃E₃ – Y₂E₂ – J

Подставим численные значения:

0,1 V₂ – 0,0167 V₃ = 0,6

0,0167 V₂ – 0,0817 V₃ = –4,22

V₂ – 0,167 V₃ = 6

V₂ – 4,9 V₃ = –253,2

4,733 V₃ = 259,2

V₃ = 54,761 В

V₂ = 6 + 0,167 V₃ = 15,127 В

Подставим эти значения в выражения для токов в ветвях:

I₁ = Y₁ (E₁ – V₂) = 0,0333*(18 – 15,127) = 0,096 А

I₂ = Y₂ (E₂ – V₃) = 0,04*(28 – 54,761) = –1,07 А

I₃ = Y₃ (E₃ – V₃) = 0,025*(32 – 54,761) = –0,569 А

I₄ = Y₄ (V₃ – V₂) = 0,0167*(54,761 – 15,127) = 0,661 А

I = Y V₂ = 0,05*15,127 = 0,756 А.

Таблица 1. Результаты расчетов.

Ток	Значение по методу контурных токов, А	Значение по методу узловых потенциалов, А
I1	0,096	0,096
I2	–1,07	–1,07
I3	–0,569	–0,569
I4	0,661	0,661
I	0,757	0,756

Вывод: оба метода расчета дают одинаковые результаты с точностью до ошибки счета.

Определение тока в резисторе R методом эквивалентного источника.

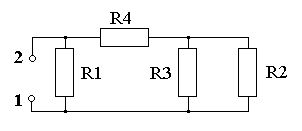
Для определения тока в ветви R необходимо эту ветвь разомкнуть (рис. 2.2), а часть цепи, подключенную к этой ветви, заменить эквивалентным источником с э.д.с. Е_экв и внутренним сопротивлением R_экв (рис. 2.3).

Е_экв равно напряжению на зажимах разомкнутой ветви (напряжение холостого хода) Е_экв = U₂₁ = V₂ – V₁. R_экв равно входному сопротивлению пассивной цепи относительно зажимов (пассивная цепь получается из данной исключением источников, причем э.д.с. замыкаются накоротко, а источники тока разрываются-удаляются)

Тогда по закону Ома I_R = U₂₁ /(R_экв + R)

Рис. 2.2. Развернутая схема эквивалентного источника в режиме холостого хода.

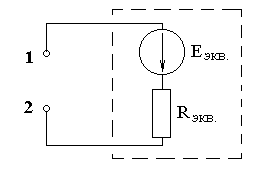
Рис. 2.3. Эквивалентная схема источника.

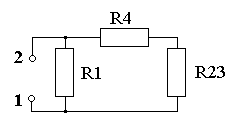
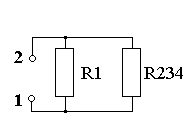
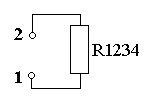
Рис. 2.4. Пассивная цепь	Рис. 2.5.	Рис. 2.6.	Рис. 2.7.

Последовательность преобразования пассивной цепи для расчета R_экв. = R₁₂₃₄ (рис. 2.4 – 2.7).

R₂₃ = R₂ R₃ /(R₂ + R₃) = 40*25/(40+25) = 15,38 Ом

R₂₃₄ = R₂₃ + R₄ = 15,38 + 60 = 75,38 Ом

R_экв. = R₁₂₃₄ = R₁ R₂₃₄ /(R₁ + R₂₃₄) = 30*75,38 /(30+75,38) = 21,46 Ом

Определяем U₂₁ методом контурных токов

I₁₁ (R₁ + R₃ + R₄) + I₂₂ R₃ + JR₃ = E₁ – E₃

I₂₂ (R₂ + R₃) + I₁₁ R₃ + JR₃ = E₂ – E₃

130 I₁₁ + 40 I₂₂ + 92 = –14

65 I₂₂ + 40 I₁₁ + 92 = –4

I₁₁ = (–96 – 65 I₂₂) / 40 = –2,4 – 1,625 I₂₂

130*(–2,4 – 1,625 I₂₂) + 40 I₂₂ + 92 = –14

–171,25 I₂₂ = 206

I₂₂ = –1,203 А

I₁₁ = –2,4 – 1,625 I₂₂ = –0,445 А

E_экв = U₂₁ = E₁ – I₁₁R₁ = 18 + 0,445*30 = 31,35 В

I_R = E_экв /(R_экв + R) = 31,35 / (21,46 + 20) = 0,756 А.

Баланс мощностей.

P_нагр. = I₁²R₁ + I₂²R₂ + I₃²R₃ + I₄²R₄ + I_R²R = 0,096²*30 + 1,07²*25 + 0,569²*40 + 0,661²*60 + + 0,756²*20 = 79,5 Вт

P_ист. = E₁I₁ + E₂I₂ + E₃I₃ + V₃J = 18*0,096 – 28*1,07 – 32*0,569 + 54,761*2,3 = 79,51 Вт

Мощность, выделяемая в резисторах, с точностью до погрешности вычислений, равна мощности, отбираемой от источников.

Задача 1.3. В цепи (рис. 3.1) действует независимый источник напряжения с ЭДС Е = 50 мкВ и зависимый источник тока J = H I₂ , где H = 0,45. Рассчитать напряжение U₄₅ .

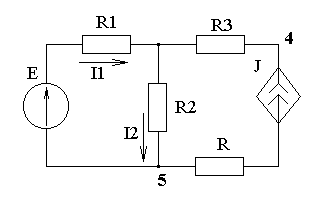
Рис. 3.1. Схема цепи.

E, мкВ	R, Ом	R1, Ом	R2, Ом	R3, Ом
50	10	10	10	30

Решение.

По правилам Кирхгофа,

I₁R₁ + I₂R₂ = E

I₁ + 0,45 I₂ = I₂

I₁ = 0,55 I₂

10*0,55 I₂ + 10*I₂ = 50

15,5*I₂ = 50

I₂ = 3,226 мкА

Напряжение U₄₅ = I₂R₂ + JR₃ = 3,226*10 + 0,45*3,226*30 = 75,8 мкВ.

Задача 1.4. Задан двухполюсник (рис. 4.1). Параметры: R=5 Ом, L= 50 мкГн, C= 0,1 мкФ. На входе двухполюсника действует источник гармонической ЭДС u(t) = U_m * cos ( w t + y).

U_m = 4 В, f = 180 кГц , y = –30.

1. Записать комплексные сопротивления Z₁, Z₂, Z₃ и рассчитать эквивалентное комплексное сопротивление Z_эк.

2. Используя комплексные числа, рассчитать комплексные токи I, I₁, I₂ и комплексные напряжения на всех элементах цепи.

3. На комплексной плоскости привести векторную диаграмму токов I, I₁, I₂.

4. Записать выражения для мгновенных значений токов i(t) , i₁(t) , i₂(t) и напряжения на резисторе u_R(t).

5. Построить график зависимости от времени i(t) и u(t).

6. Рассчитать баланс активной и реактивной мощностей.

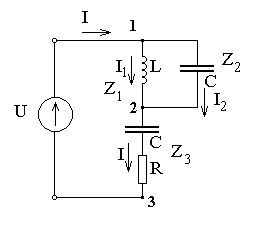
Рис. 4.1. Схема включения двухполюсника.

Решение.

Считаем, что данное значение U_m – действующее.

Определяем круговую частоту: w = 2pf = 2 * 3,14 * 180 * 10³ = 1,131 * 10⁶ рад/сек.

X_C = 1/(wC) = 1/(1,131*10⁶*0,1*10^–6) = 8,84 Ом

X_L = wL = 1,131*10⁶*50*10^–6 = 56,55 Ом

Z₁ = j X_L = j*56,55 = 56,55 e ^{j 90°} Ом

Z₂ = –j X_C = –j*8,84 = 8,84 e ^{–j 90°} Ом

Z₃ = R – j X_C = 5 – j*8,84 = 10,16 e ^{–j 60,5°} Ом

Z_эк (входное сопротивление) – сопротивление между точками 1 и 3:

Z₁₂ = ( Z₁ *Z₂ )/( Z₁ + Z₂ ) = j*56,55*(–j*8,84) / (j*56,55 – j*8,84) = –j*10,48 = 10,48 e ^{–j 90°} Ом

Z_эк = Z_вх = Z₁₃ = Z₁₂ + Z₃ = –j*10,48 + 5 – j*8,84 = 5 – j*19,32 = 19,96 e ^{–j 75,5°} Ом

Запишем входное напряжение в комплексной форме:

y = –30°

U = U₁₃ = U_m e ^jy = 4 e ^{–j 30°} В.

I = U₁₃ / Z_эк = 4 e ^{–j 30°} / 19,96 e ^{–j 75,5°} = 0,2 e ^{j 45,5} А

U₂₃ = I * Z₃ = 0,2 e ^{j 45,5} * 10,16 e ^{–j 60,5°} = 2,036 e ^{–j 15} В

U₁₂ = I * Z₁₂ = 0,2 e ^{j 45,5} * 10,48 e ^{–j 90°} = 2,1 e ^{–j 44,5} В

I₁ = U₁₂ / Z₁ = 2,1 e ^{–j 44,5} / 56,55 e ^{j 90°} = 0,037 e ^{–j 134,5} А

I₂ = U₁₂ / Z₂ = 2,1 e ^{–j 44,5} / 8,84 e ^{–j 90°} = 0,237 e ^{j 45,5} А

Напряжения на элементах цепи:

U_L = U_С1 = U₁₂ = 2,1 e ^{–j 44,5} В

U_С2 = I * Z_C = 0,2 e ^{j 45,5} * 8,84 e ^{–j 90°} = 1,772 e ^{–j 44,5} В

U_R = I * R = 0,2 e ^{j 45,5} * 5 = 1,002 e ^{j 45,5} В

Мгновенные значения напряжений и токов:

u_вх(t) = U_m cos (wt + y) = 5,657 cos (1,131·10⁶ t – 30°) В.

i(t) = i₃(t) = |I| cos (wt + y₃) = 0,283 cos (1,131·10⁶ t + 45,5°) А.

i₁(t) = |I₁| cos (wt + y₁) = 0,052 cos (1,131·10⁶ t – 134,5°) А.

i₂(t) = |I₂| cos (wt + y₂) = 0,335 cos (1,131·10⁶ t + 45,5°) А.

u_R(t) = |U_R| cos (wt + y_R) = 1,417 cos (1,131·10⁶ t + 45,5°) В.

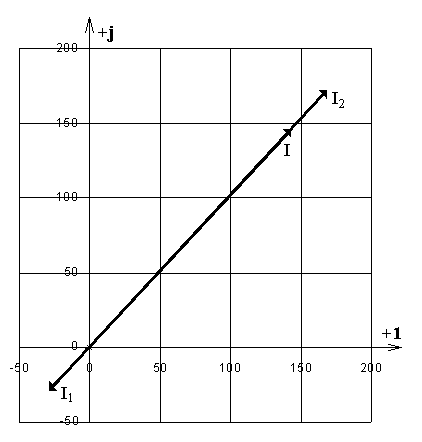
Рис. 4.2. Векторная диаграмма токов (I – в мА).

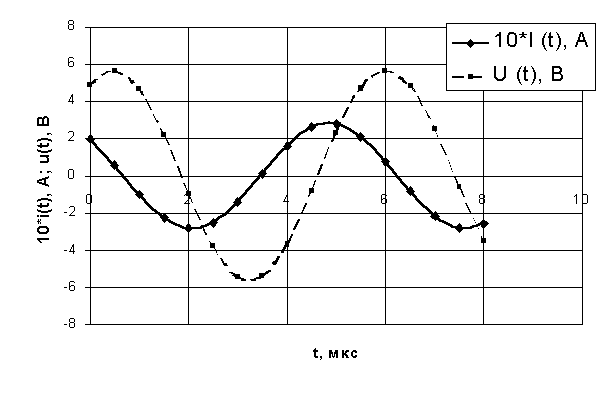
Рис. 4.3. Графики i(t), u_вх(t).

Комплексная мощность, потребляемая от источника:

S = U I^* = 4 e ^{–j 30°}· 0,2 e ^{–j 45,5} = 0,802 e ^{–j 75,5} Вт = 0,201 – 0,776 j

Активная мощность:

Р = Re ( S ) = 0,201 мВт

Проверка – на резисторе выделяется Р_R = I² R = 0,2² * 5 = 0,2 Вт

Реактивная мощность от источника:

Q = Im ( S ) = –0,776 Вт

Реактивные мощности приемников:

Q_L = I₁² * X_L = 0,037² * 56,55 = 0,077 Вт

Q_С1 = I₂² * X_С = 0,237² * 8,84 = 0,497 Вт

Q_С2 = I² * X_С = 0,2² * 8,84 = 0,354 Вт

Q = Q_L1 – Q_С1 – Q_С2 = –0,774 Вт.

Баланс активных и реактивных мощностей выполняется с точностью до ошибки вычислений.

Задача 1.5. Задана схема, показанная на рис. 5.1.

Параметры: Х_м=30 Ом, i(t) = 10 cos ( t – 190) мА

R₁ = 40 Ом, R₂ = 50 Ом, Х_L = 90 Ом, Х_C = 80 Ом.

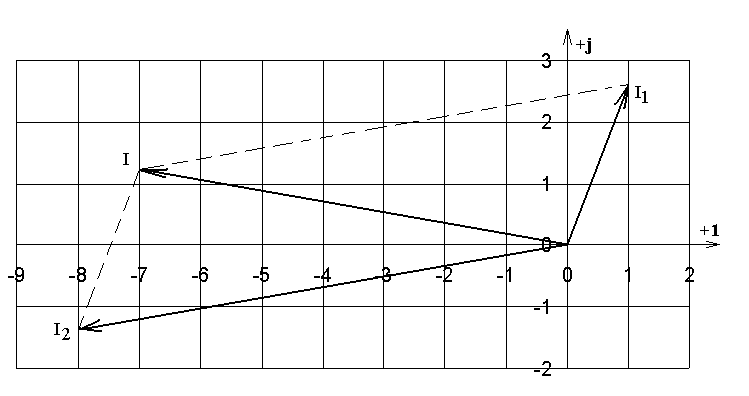
1. Вычислить комплексные значения токов всех ветвей схемы. Показать эти значения на векторной диаграмме.

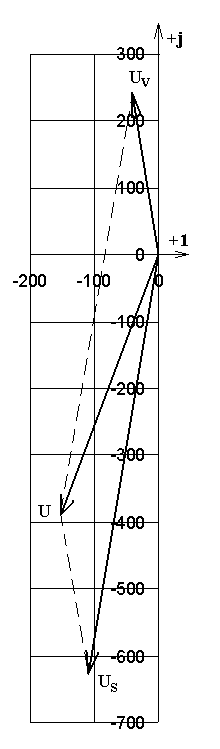
2. Рассчитать комплексные значения напряжения на индуктивном элементе, примыкающем к источнику тока. Построить векторную диаграмму напряжения на индуктивности, примыкающей к источнику тока. На диаграмме должны быть показаны отдельно векторы всех составляющих напряжения (самоиндукции и взаимной индукции) индуктивности и вектор результирующего напряжения на этом элеменете.

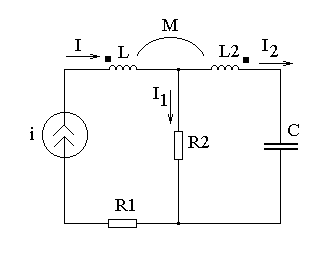
Рис. 5.1. Схема цепи.

Решение.

I = (10/)·e ^{– j 190} = 7,071 e ^{j 170} мА.

Выберем предполагаемые направления токов в ветвях. Составляем уравнения по законам Кирхгофа:

I = I₁ + I₂

U_R2 = U_L2 + U_C

Напряжение на индуктивности складывается из напряжения самоиндукции и напряжения взаимоиндукции, поскольку катушки включены противонаправленно, напряжения складываются:

U_L = j X_L I – j X_M I₂

U_L2 = j X_L2 I₂ – j X_M I

Тогда система уравнений для определения токов I₁ и I₂ приобретает вид:

I₁ + I₂ = I

R₂ I₁ = j X_L2 I₂ – j X_M I – j X_C I₂

Подставим заданные числовые значения:

I₁ + I₂ = 7,071 e ^{j 170}

50 I₁ = j 90 I₂ – j 212,13 e ^{j 170} – j 80 I₂

50*(7,071 e ^{j 170} – I₂) = j 90 I₂ – j 212,13 e ^{j 170} – j 80 I₂

50 I₂ + j 10 I₂ = 353,55 e ^{j 170} + j 212,13 e ^{j 170}

50,99 e ^{j 11,3} I₂ = 412,31 e ^{–j 159}

I₂ = 8,086 e ^{–j 170,3} мА.

I₁ = I – I₂ = 7,071 e ^{j 170} – 8,086 e ^{–j 170,3} = –6,964 + j 1,228 + 7,97 + j 1,362 = 1,006 + j 2,59 = = 2,779 e ^{j 68,8} мА.

Напряжение самоиндукции на индуктивности, примыкающей к источнику тока (левой)

U_S = j X_L I = j 90 * 7,071 e ^{j 170} = 636,39 e ^{–j 100} мВ.

Напряжение взаимоиндукции на индуктивности, примыкающей к источнику тока (левой)

U_V = –j X_M I₂ = –j 30 * 8,086 e ^{–j 170,3} = 242,58 e ^{j 99,7} мВ.

U_L = j X_L I – j X_M I₂ = 636,39 e ^{–j 100} + 242,58 e ^{j 99,7} = –110,51 – j 626,71 – 40,87 + j 239,11 = = –151,38 – j 387,6 = 416,1 e ^{–j 111,3} мВ.

Рис. 5.2. Векторная диаграмма токов.
	Рис. 5.3. Диаграмма напряжений на индуктивном элементе, примыкающем к источнику тока.

12