§3.3. Преобразование интервалов длины, времени и скоростей.

В пункте 3.2. были получены преобразования Лоренца. С их помощью можно получить и обратные выражения:

Рассмотрим изменение пространственного интервала вдоль оси .

Пусть стержень расположен вдоль оси и неподвижен.

Координаты в системе можно определять в различные моменты времени, так как стержень неподвижен. Для определения длины стержня, координаты надо определять в один и тот же момент времени:

Определим значения временного интервала между двумя событиями, при переходе в другую систему отсчета.

Пусть временной интервал определяется часами, которые неподвижны.

Тогда интервал времени определяется часами и будет равен: (в системе), и( в системе).

Определим проекцию :

;

Определим :

§3.4. Релятивистская динамика.

Уравнение движения материальной точки в классической динамике, имеет вид:

(сила действующая на точку, а- ее импульс)

Предполагается, что не зависит от скорости.

В теории относительности, уравнение движения точки имеет такой же вид, но при этом учитывается, что масса точки зависит от скорости.

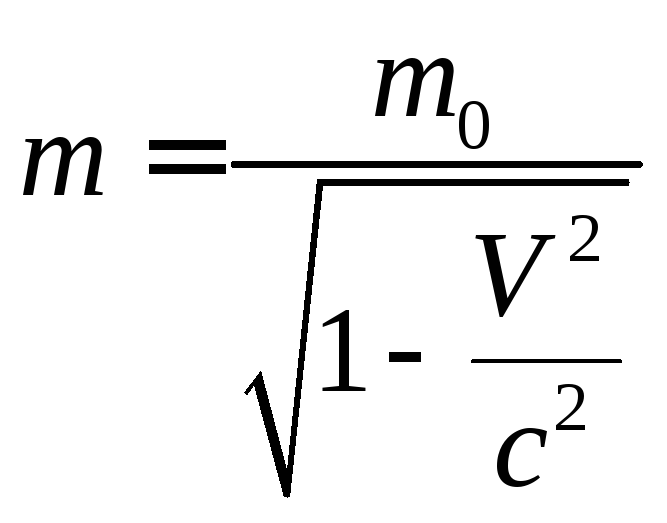, где- скорость точки, а- масса точки при.

Рассмотрим частицу, скорость которой :

Пусть ее скорость изменяется от 0 до , тогда.

Если потенциальной энергии нет, то на такую же величину измененится .

Известно, что , тогда:

В правой части равенства, стоит величина, которая не зависит от выбора системы отсчета, отсюда следует, что в левой части равенства стоит такая же величина.

Где- импульс и энергия частицы в системе, а- импульс и энергия частицы в системе.

§3.5 Четырех - векторы.

В классическом приближении, радиус-вектор и т. д., принято считать векторами. В этом приближении, длина этих векторов не зависит от выбора системы отсчета. На самом деле, длина этих векторов будет изменяться.

В этом легко убедиться, вычислив:

Это означает, что радиус вектор материальной точки вектором не является.

Легко убедиться, что:

Такая квадратичная форма не зависит от выбора системы отсчета и ее можно рассмотреть как квадрат модуля некоторого вектора, проекции которого на оси координат будут . Так как таких проекций – четыре, то оказывается, вектор находится в четырехмерном пространстве и его принято называть – четырех - вектор радиус-вектор.

В четырехмерном пространстве, система вращается относительно системы, вокруг их общего начала.

Таким образом, из преобразований Лоренца следует, что векторами можем пользоваться только в четырехмерном пространстве, а в трехмерном – приближенно.

Отсюда возникло предположение, что наше пространство четырехмерное. Как оказалось впоследствии – это так.

Эйнштейн предположил, что любое тело, с достаточно большой массой искривляет пространство, что приводит к изменению траектории движения.

При переходе из одной системы отсчета в другую, проекции любого вектора должны преобразовываться по одинаковым правилам.

Преобразования радиус-вектора, при переходе из одной системы отсчета – преобразования Лоренца.

;;;

В пункте 3.4 было показано, что не зависит от выбора системы отсчета, отсюда следует, что ее можно рассматривать как квадрат длины некоторого четырех – вектора с проекциями, где- четырех – вектор импульса.

Очевидно, что он будет преобразовываться по тем же самым формулам.