
- •По теме: механика, магнитостатика, электродинамика.
- •Глава 3. Специальная теория относительности.
- •Часть II
- •Глава 1. Электростатика
- •Глава 2. Магнитостатика
- •Глава 3. Электродинамика.
- •Часть 1. Механика.
- •Глава 1. Кинематика.
- •§ 1.1 Кинематика материальной точки.
- •2) Векторное произведение (вектор, направленный перпендикулярно к каждому из векторов)
- •§ 1.2 Кинематика твердого тела.
- •Глава 2. Динамика.
- •§ 2.1 Динамика материальной точки. Понятие массы и силы.
- •§ 2.2 Импульс. Закон сохранения импульса. Центр масс.
- •§2.3 Момент импульса. Закон сохранения момента импульса.
- •§2.4 Работа и энергия.
- •§2.5 Динамика твердого тела, закрепленного на оси.
- •§2.6 Кинетическая энергия вращающегося тела. Теорема Штейнера - Гюйгенса.
- •§ 2.7. Динамика твердого тела с неподвижной точкой. Уравнение Эйлера.
- •§ 2.8. Динамика произвольного движения твердого тела.
- •§2.9. Явление прецессии. Гироскопы.
- •Глава 3. Специальная теория относительности.
- •§ 3.1. Принцип относительности.
- •§3.2. Преобразования Лоренца.
- •§3.3. Преобразование интервалов длины, времени и скоростей.
- •§3.4. Релятивистская динамика.
- •§3.5 Четырех - векторы.
- •§3.6 Преобразование силы.
- •§ 1.2 Теорема Остроградского-Гаусса
- •§1.3 Электрический потенциал.
- •§ 1.4 Энергия электростатического поля
- •§ 1.5 Электрическое поле диэлектрика
- •§ 1.6 Электрическое поле на границе двух диэлектриков
- •§ 1.7 Проводники в электростатическом поле.
- •§ 1.8 Ёмкость конденсатов
- •§ 1.9 Электрический ток в уравнении непрерывности
- •§ 1.10 Закон электрического тока.
- •Глава II Магнитостатика.
- •§2.1 Силы Лоренца и Ампера
- •§2.2 Магнитное поле прямого проводника с током.
- •2.3 Закон полного тока. Теорема о циркуляции.
- •§2.4 Плотность источника магнитного поля.
- •§2.5 Закон Био-Савара-Ласпласа.
- •Глава III Электродинамика
- •§3.1 Преобразование полей
- •§3.2 Электромагнитная индукция.
- •§3.3 Взаимная индукция. Самоиндукция. Индуктивность.
- •§ 3.4Уравнение Максвелла.
§ 1.5 Электрическое поле диэлектрика
Рассмотрим систему зарядов
![]() ,
которая отличается осиOв небольшой области пространства.
,
которая отличается осиOв небольшой области пространства.
Поместим в эту область начало
системы отсчёта и определим потенциал
в точке.
![]()
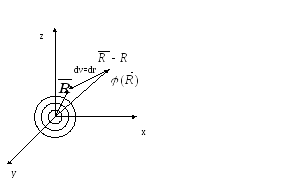

![]()
* * *
![]()
a>>x
![]()
* * *
Так как R0>>R, то подынтегральную функцию мы можем переставить в виде степенного ряда.
![]()

![]()
Т.о. первый член ряда определяет потенциал по форме точечного заряда. Второй член ряда на много меньше 1го и его вклад будет несущественным, за исключением того случая, когда общий заряд системы q=0, и тогда потенциал будет определяться 2-ым членом ряда, который называется-дипольный момент.
![]()
Пример: Определим дипольный момент заряда

![]()
Диэлектриком называют тела, заряды которых связаны между собой в неразрывные цепи
Рассмотрим неполимерный диэлектрик.
В таком диэлектрике отрицательный заряд
атома расположен сферически, симметрично
относительно ………………………
 В отсутствии внешних полей диэлектрик
дипольный момент такого атома равен
0, так как
В отсутствии внешних полей диэлектрик
дипольный момент такого атома равен
0, так как![]()
Если диэлектрик поместить в электрическое поле, то симметрическа картина нарушиться.
 В этом случаи у атома появляется
дипольный момент
В этом случаи у атома появляется
дипольный момент![]()
![]() ,
который совпадает с направление вектора
,
который совпадает с направление вектора![]() и диэлектрик становиться поляризованным.
и диэлектрик становиться поляризованным.
Полярные диэлектрики
Отрицательные и положительные
заряды атома располагаютсянесимметрично и каждый атом обладает
дипольным моментом. Но в отсутствии
внешнего поля![]() разряд
атомов расспологаеться хаотически и
разряд
атомов расспологаеться хаотически и![]()
Если поместить диэлектрик во внешние
электрическое поле, то дипольный моменты
орентир. Вдоль поля и диэлектрик
становиться поляризованным. Для
характеристики полеризированного
диэлектрика вводят вектор «поляризированность»
![]() ,
который равен суммарному дипольному
моменту единиц объёма проводника.
,
который равен суммарному дипольному
моменту единиц объёма проводника.
Для определения этого вектора разобьём весь диэлектрик на вdv. Определим суммарный дипольный момент в каждом из этих объёмов, тогда векторполяризизированности
![]()
Процесс возникновения дипольного момента у диэлектрика называется померид
Рассмотри плоскую поверхность dsвнутри диэлектрика. Поместим……в электрическое поле и определим какой положительный заряд был перенесён через эту поверхность приполяризации диэлектрика

При померизации диэлектрика через
поверхность dsпройдут
заряды только тех диполей, которые до
поляризации находил внутри объёма
параллельно объём, которыхds*decos![]()
Если в единицу объема диэлектрика
было к диполей, а заряд каждого диполя
q, то через поверхностьdsбудет перенесён заряд![]() cos
cos![]() =
=![]()
![]()
Так как вектор поляризациовонность
![]() то
заряд, поляризации будет перенесён
черезds
то
заряд, поляризации будет перенесён
черезds
![]()
Рассмотрим объём Vвнутри диэлектрика, который ограниченно замкнут поверхностьюS. Определённый заряд, который есть внутри объёма М при потери диэлектрика.
Для этого разобьём по SнаdS/ Вычислим заряд
перенесённый через каждый участок по
формуле![]() , и затем сложим тогда внутри объёмаVост. Заряд Ур. Знака
, и затем сложим тогда внутри объёмаVост. Заряд Ур. Знака
![]() - Этот заряд
называется поляризованным. Его можно
за……
- Этот заряд
называется поляризованным. Его можно
за……
![]()
![]() -
плотность поляризованных зарядов
-
плотность поляризованных зарядов
![]()
![]()
Так как это рав выю для любого V, то
![]()
Пусть в диэлектрике находиться другой заряд(сторонний) кроме зарядов самого диэлектрика
Пусть пл. стор. Зряда –q0тогда

![]() -
вектор электрического смещения или
вектор электрического индукции
-
вектор электрического смещения или
вектор электрического индукции
![]()
Мы будем рассматривать только
такие диэлектрики для которых вектор
![]() пропорционален вектор
пропорционален вектор![]()
![]()
H- диэлектрическая восприимчивость
![]()
![]() ;
диэлектрическая проницаемость
;
диэлектрическая проницаемость
Вычислим поток
![]() через произвольную замкнутую поверхность
через произвольную замкнутую поверхность
![]()
q0- сумма всех сторон зарядов, которые находиться внутри поверхности
Энергетическая система зарядов определённых по форме
![]() (§1.4)
(§1.4)
Если заряды находиться в диэлектрике то :
![]()

