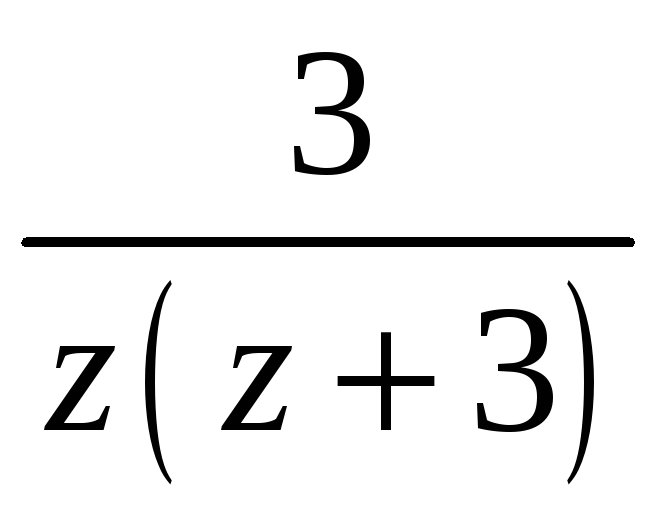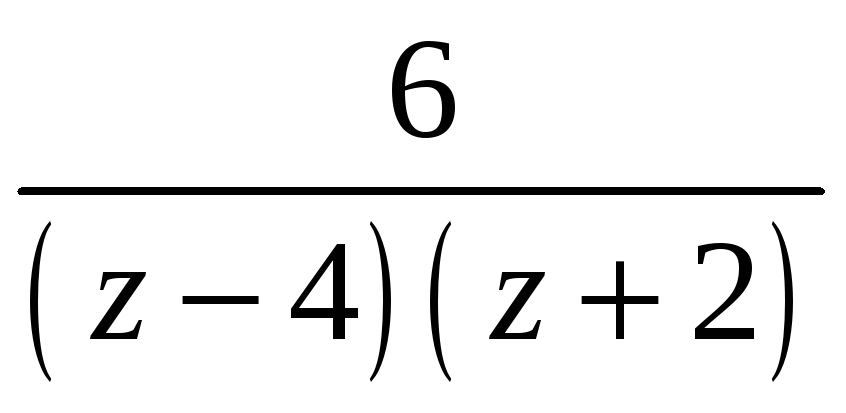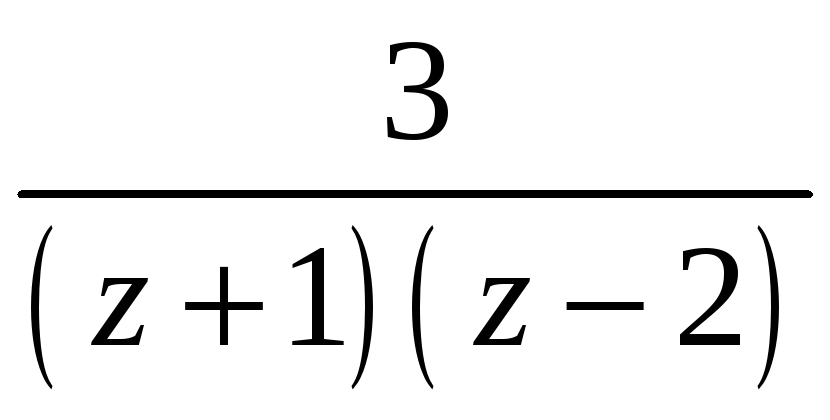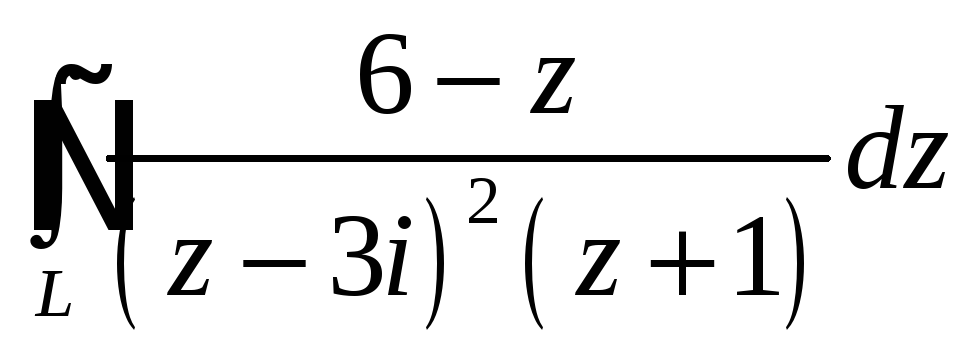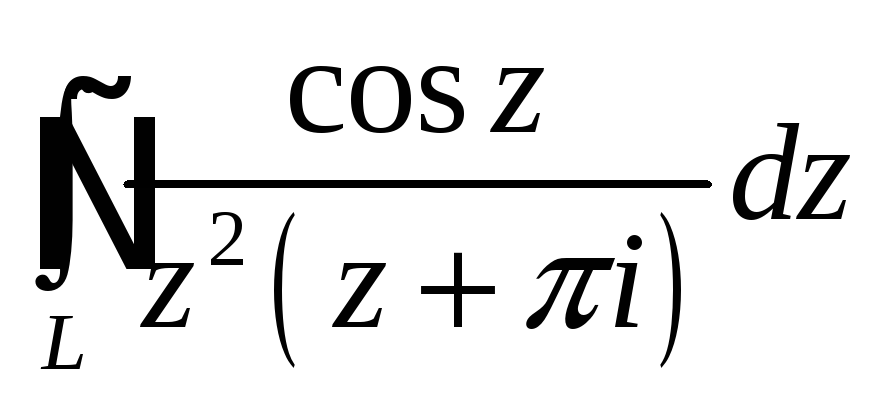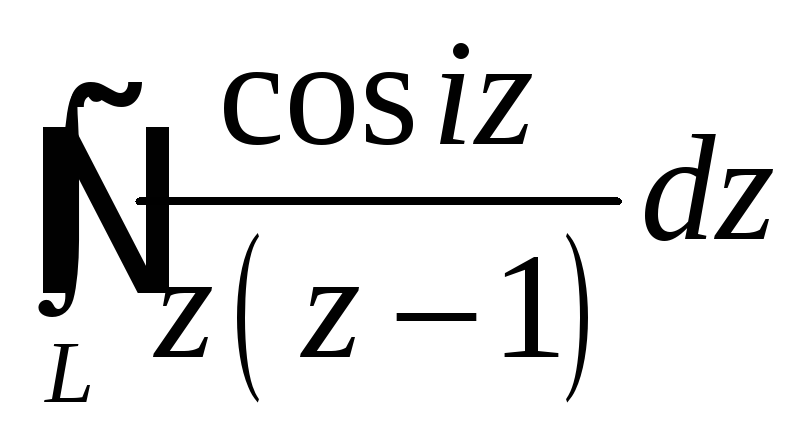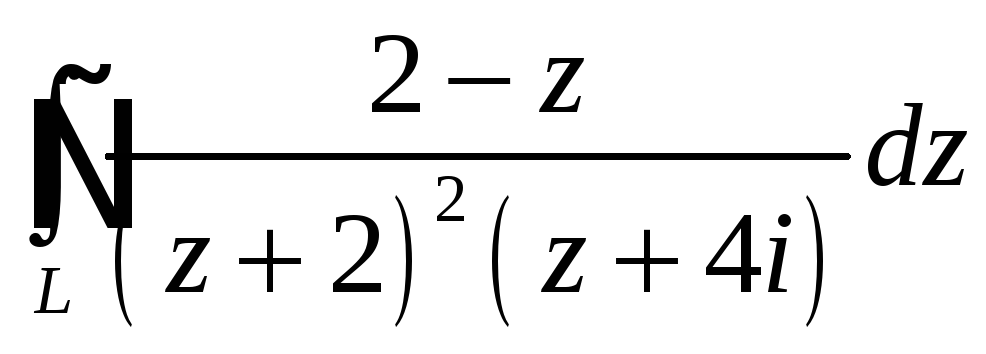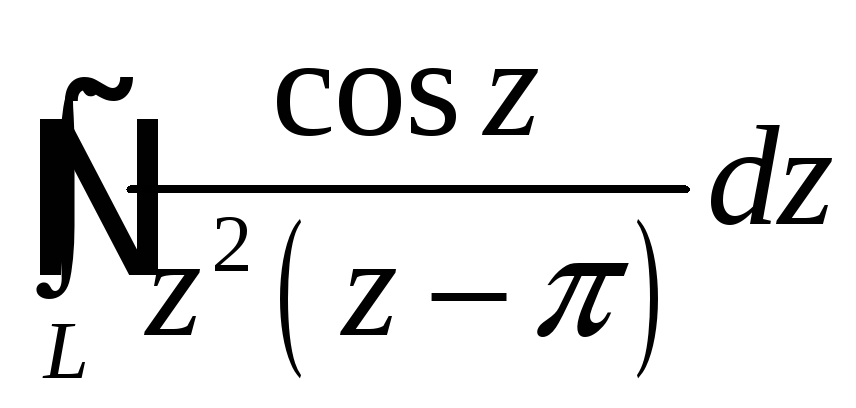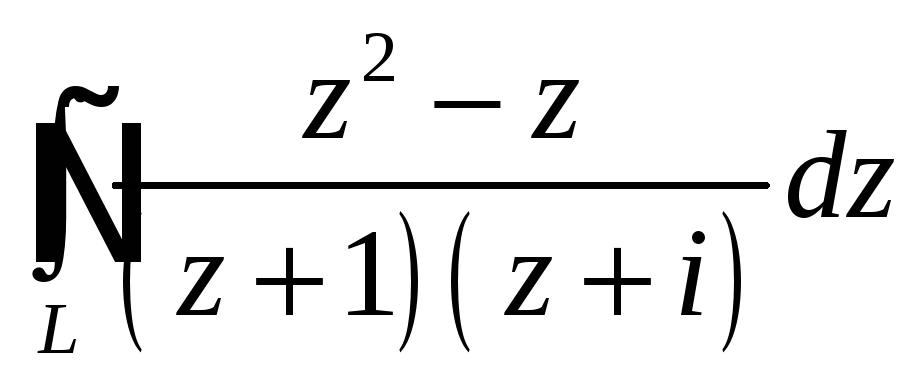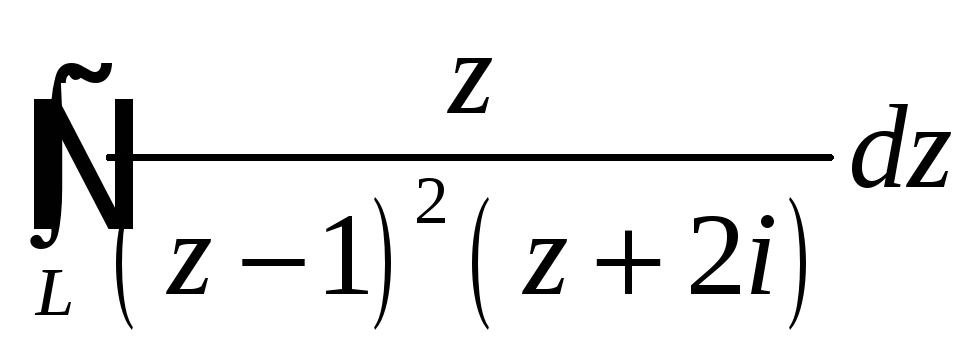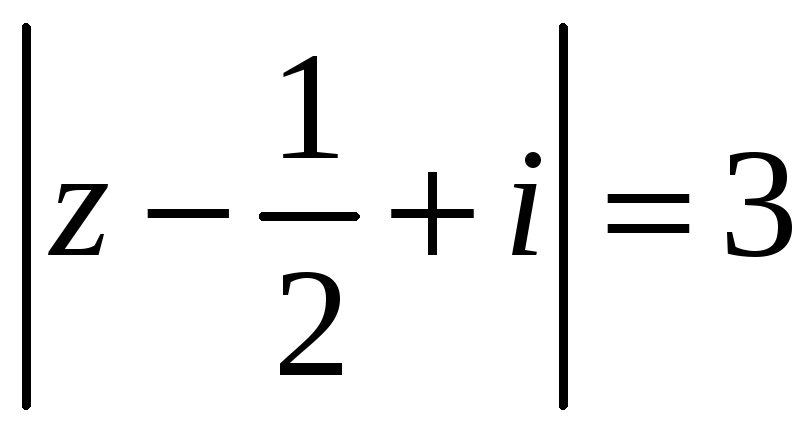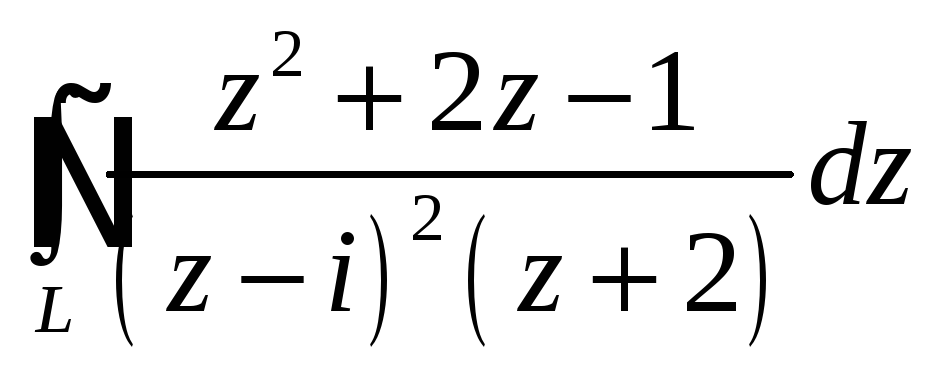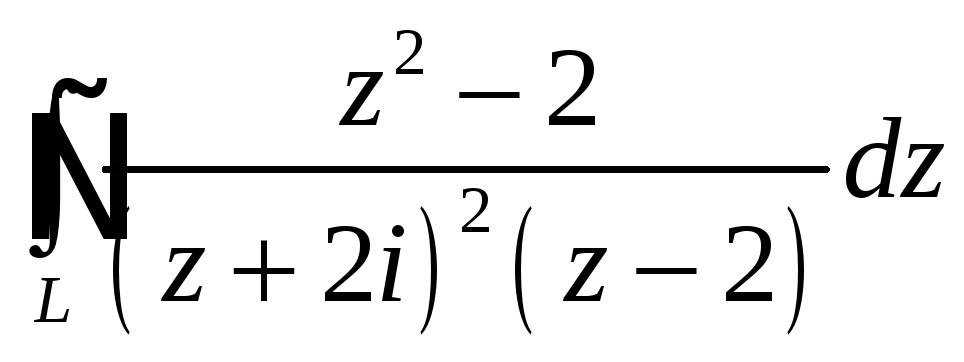Задача 4 Варианты 00–19

Разложить функцию в ряд Тейлора в окрестности заданной точки и определить область существования полученного разложения.

Вари- анты	Функция		Вари- анты	Функция
00			10
01			11
02			12
03			13
04			14
05			15
06			16
07			17
08			18
09			19

Варианты 20–29

Определить область (круг) сходимости данного ряда и исследовать его сходимость (расходится, сходится условно, сходится абсолютно) в точках , и .

Вари- анты	Ряд
20
21
22
23
24
25
26
27
28
29

Задача 5

При помощи теоремы о вычетах вычислить данный интеграл по контуру .

Вари- анты	Интеграл	Контур
00
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

9