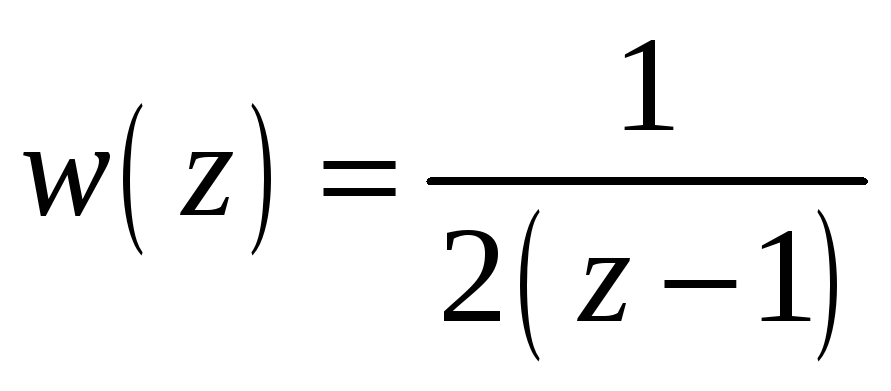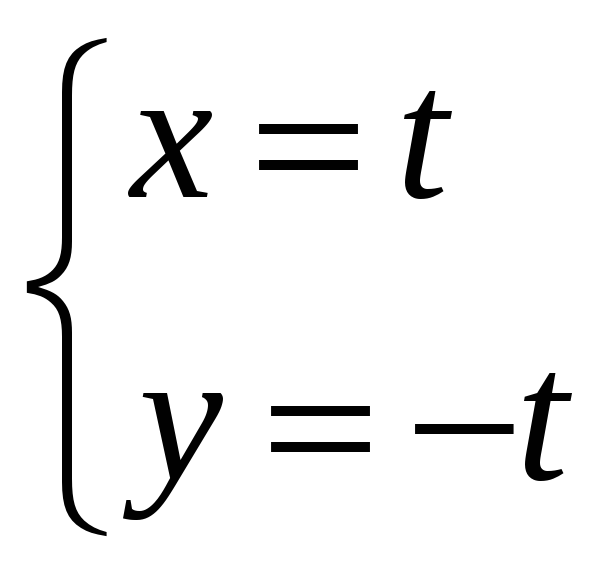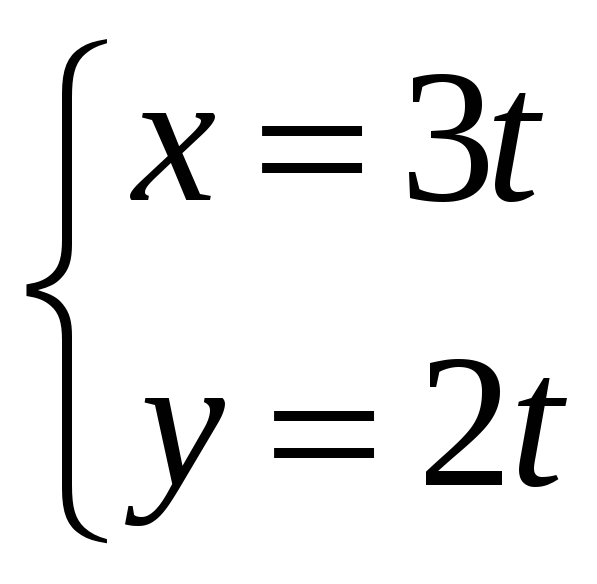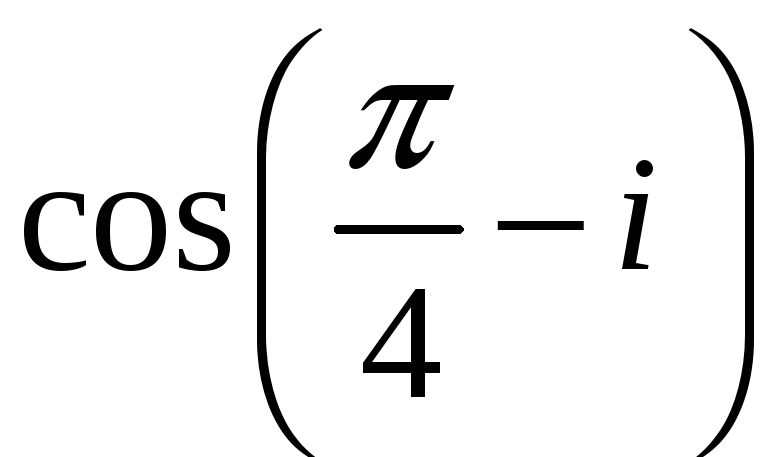Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:Задачи ТФКП.doc
Задания для самостоятельного решения Задача 1
В плоскости
![]() дано уравнение линии
дано уравнение линии
![]() .
На какую линию плоскости
.
На какую линию плоскости
![]() она отображается функцией
она отображается функцией
![]() ?
Привести поясняющие чертежи.
?
Привести поясняющие чертежи.
|
Вари- анты |
Уравнение
линии
|
Функция
|
Вари- анты |
Уравнение
линии
|
Функция
|
|
00 |
|
|
15 |
|
|
|
01 |
|
|
16 |
|
|
|
02 |
|
|
17 |
|
|
|
03 |
|
|
18 |
|
|
|
04 |
|
|
19 |
|
|
|
05 |
|
|
20 |
|
|
|
06 |
|
|
21 |
|
|
|
07 |
|
|
22 |
|
|
|
08 |
|
|
23 |
|
|
|
09 |
|
|
24 |
|
|
|
10 |
|
|
25 |
|
|
|
11 |
|
|
26 |
|
|
|
12 |
|
|
27 |
|
|
|
13 |
|
|
28 |
|
|
|
14 |
|
|
29 |
|
|
Задача 2 Варианты 00–13
Выделив в данной
функции
![]() действительную и мнимую части, выяснить,
аналитическая ли она. Вычислить значение
действительную и мнимую части, выяснить,
аналитическая ли она. Вычислить значение
![]() (выделить действительную и мнимую части)
при данном значении аргумента
(выделить действительную и мнимую части)
при данном значении аргумента
![]() .
.
|
Вари- анты |
Функция
|
|
Вари- анты |
Функция
|
|
|
00 |
|
|
07 |
|
|
|
01 |
|
|
08 |
|
|
|
02 |
|
|
09 |
|
|
|
03 |
|
|
10 |
|
|
|
04 |
|
|
11 |
|
|
|
05 |
|
|
12 |
|
|
|
06 |
|
|
13 |
|
|
Соседние файлы в предмете Теория функций комплексного переменного