Тема 6 . Статистические методы изучения взаимосвязи между явлениями. Корреляционно-регрессионный анализ.
Цель занятия: Ознакомится с различными видами корреляционного и регрессионного анализа.
6.1. Парная корреляция
Наиболее простая аналитическая
связь между результативным и факторным
признаками может описываться уравнением
прямой: 
a0 +
a1x .
Определение параметров уравнения регрессии:
; 
.
Определение линейного коэффициента корреляции:
Задача 6.1 По данным о доходах и прибыли построить уравнение связи, измерить тесноту связи между прибылью и доходами, провести полный корреляционно- регрессионный анализ связи.
Исходные данные и расчеты Таблица 6.1
-
№
Доходы, млрд. руб.
Прибыль, млрд. руб.
Х2
ХУ
У2
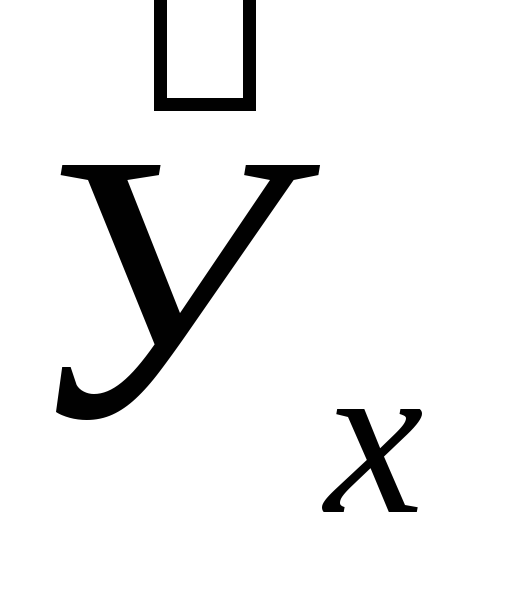
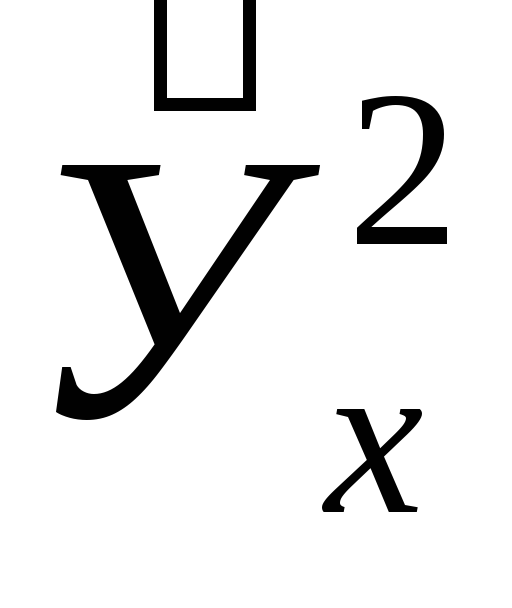
1
5
2
25
10
4
2,116
4,480
2
13
5
169
65
25
4,747
22,534
3
24
7
576
168
49
8,364
69,953
4
18
6
324
108
36
6,391
40,845
5
20
8
400
160
64
7,049
49,683
6
30
12
900
360
144
10,337
106,845
7
32
10
1024
320
100
10,994
120,872
142
50
3418
1191
422
49,998
415,212
Уравнение прямой:
a0+ a1x. 
0,4726
+ 0,3288х
Параметры уравнения:
;
.
С увеличением доходов (х) на 1 млрд. руб. прибыль (у) в среднем увеличивается на 0,3288 млрд. руб.
Линейный коэффициент корреляции:
=
Связь прямая, сильная.
Коэффициент эластичности:
С
увеличением доходов (х) на 1% прибыль (у)
в среднем увеличивается на 0,9338%.
β-коэффициент:
-коэффициент показывает, что на 0,9464 среднего квадратического отклонения σу
изменяется результативный признак у при изменении фактора на величину его среднего
квадратического отклонения σх.
Значимость линейного коэффициента корреляцииопределяется по
t – критерию Стьюдента:
tкрит.
определяется по таблице «Значение t
– критерия Стьюдента при уровне
значимости 
=
0,05 и степени свободы 
равно 2,574.
Соотношения: tрасч > tкрит выполняется, значит линейный коэффициент корреляции значим.
Измерение тесноты связи через корреляционное отношение эмпирических и теоретических значений (у):
.
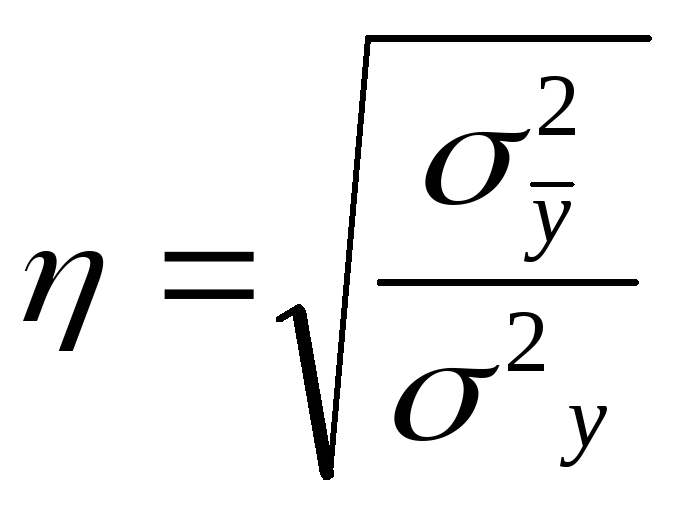
Связь прямая, сильная.
Используется при любой форме связи, прямолинейной и криволинейной.
Коэффициент детерминации R2 = 0,94642 = 0,8957,
показывает, что 89,57% вариации результативного показателя объясняется вариацией факторного показателя.
Существует связь между
линейным коэффициентом
корреляции r
и коэффициентом регрессии ai
: 
.
Уравнение прямой можно получить по диаграмме, построенной с помощью электронной таблицы.
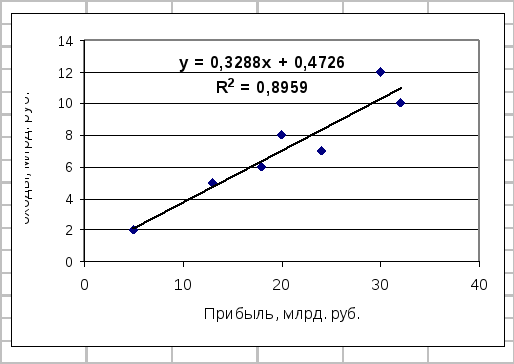
Рис. 6.1 Зависимость прибыли от доходов.
а) Определить изменение прибыли, если объем доходов увеличится на 2 млрд. руб.
в) Определить величину прибыли, если объем доходов достигнет 40 млрд. руб.
0,4726
+ 0,3288х
а) Прибыль при увеличении объем доходов увеличится на 2 млрд. руб. увеличится на
657,6 млн. руб.
∆Yx = 0,3288x*2 = 0,6576
в) Величина прибыли, если объем доходов достигнет 40 млрд. руб.
будет равна 13,625 млрд. руб. Yx =0,4726+ 0,3288*40 = 13,625
Задача 6.2 Определить тесноту связи между чистой прибылью и объемом продаж, используя коэффициент корреляции рангов (коэффициент Спирмена).
Исходные данные и расчеты Таблица 5.2
|
№ п/п
|
Объем продаж, млн. руб.
|
Чистая прибыль тыс. руб.
|
Ранжирование
|
Сравнение рангов
|
Разница рангов
|
Квадраты разниц рангов
| ||||
|
|
Xi |
Yi |
X |
Nx |
Y |
Ny |
Rx |
Ry |
di |
di² |
|
1 |
1,8 |
80 |
1,3 |
1 |
20 |
1 |
2 |
4 |
-2 |
4 |
|
2 |
2,3 |
75 |
1,8 |
2 |
42 |
2 |
3 |
3 |
0 |
0 |
|
3 |
8,6 |
200 |
2,3 |
3 |
75 |
3 |
10 |
9 |
1 |
1 |
|
4 |
1,3 |
20 |
3,5 |
4 |
80 |
4 |
1 |
1 |
0 |
0 |
|
5 |
3,5 |
107 |
3,7 |
5 |
107 |
5 |
4 |
5 |
-1 |
1 |
|
6 |
3,8 |
125 |
3,8 |
6 |
125 |
6 |
6 |
6 |
0 |
0 |
|
7 |
4,5 |
140 |
4,5 |
7 |
140 |
7 |
7 |
7 |
0 |
0 |
|
8 |
5,8 |
175 |
5,8 |
8 |
175 |
8 |
8 |
8 |
0 |
0 |
|
9 |
3,7 |
42 |
6,5 |
9 |
200 |
9 |
5 |
2 |
3 |
9 |
|
10 |
6,5 |
210 |
8,6 |
10 |
210 |
10 |
9 |
10 |
-1 |
1 |
|
∑ |
|
|
|
|
|
|
|
|
|
16 |
Коэффициент Спирмэна:
Связь между приведенными показателями сильная, прямая.