Тема 4 Абсолютные и относительные величины

Относительный показатель динамики I_п = П_i100/П_i-1, %.

Относительный показатель структуры d_i=Пi100/П_i %, где П_i – абсолютный уровень структурной части объекта или явления.

Задача 4.1 По исходным данным о затратах за 2010 и 2012 г.г. объяснить их изменение

за три года.

Затраты, млн. руб.	Период		Динамика, %	Структура. %
	2010 г.	2012 г.		2010 г.	2012 г.
Фонд оплаты труда	4200	4980	118,57	42,67	45,97
Отчисления на социальные нужды	1490	1290	86,58	15,14	11,91
Амортизационные отчисления	150	165	110,00	1,52	1,52
Материальные затраты	1970	2240	113,71	20,01	20,68
Электроэнергия для производственных нужд	90	96	106,67	0,91	0,89
Транспортные расходы	74	82	110,81	0,75	0,76
Прочие расходы	1870	1980	105,88	19,00	18,28
	9844	10833	110,05	100,00	100,00

Все показатели в денежном выражении являются абсолютными величинами.

Доля затрат по статьям в общей сумме затрат увеличивается, если их рост за анализируемый период выше среднего уровня по предприятию (110,05%).

Это - фонд оплаты труда, материальные затраты, транспортные расходы.

Доля затрат по статьям в общей сумме затрат уменьшается, если их рост за анализируемый период ниже среднего уровня по предприятию (110,05%)

Это - отчисления на социальные нужды, электроэнергия для производственных нужд, прочие расходы.

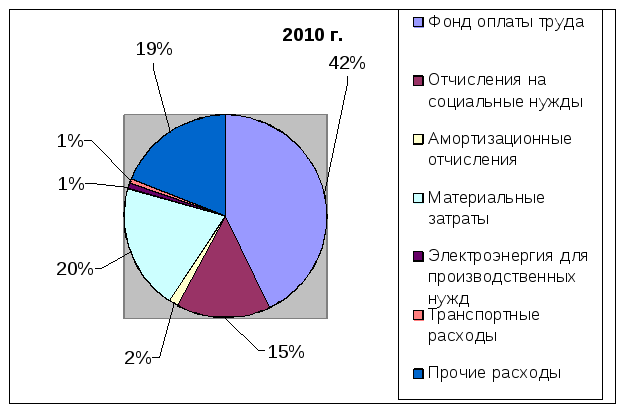
Рис. 4.1 Структура затрат в 2010 году.

Тема 5. Выборочное наблюдение

Цель занятия: Ознакомится с различными видами и способами выборочного наблюдения, а также показателями, характеризующими репрезентативность выборки.

Основные формулы для расчета показателей, характеризующих

выборочную совокупность Таблица 5.1

Показатели	обозначение	Способ выборки
		Повторный	бесповторный
Средняя ошибка выборки - для количественного признака - для доли	µх µw	или
Предельная ошибка выборки - для количественного признака - для доли
Относительная ошибка выборки - для количественного признака - для доли	βх βw
Необходимый объём выборки - для количественного признака - для доли	nx nw

Задача 5.1. Выборочное обследование длительности междугородных телефонных соединений дало следующее распределение:

Продолжительность соединения, мин.	3	5	7	9	11	13	15	17
Число обследованных, чел.	35	30	70	20	15	15	10	5

Вычислить: среднюю длительность соединения; среднюю, предельную и относительную ошибки данной выборки с вероятностью ρ = 0,997. Выборка повторная.

Решение

Расчетная таблица Таблица 5.2

	3	5	7	9	11	13	15	17	∑
	35	30	70	20	15	15	10	5	200
	105	150	490	180	165	195	150	85	1520
	740,6	202,8	25,2	39,2	173,4	437,4	547,6	441,8	2608

Средняя длительность соединения: мин.

Средняя ошибка выборки при повторной выборке:

дисперсия: , .

Предельная ошибки выборки:  = t*,

при ρ = 0,997 t = 3  = 3*,,765 мин.

Относительная ошибки выборки: %, .

Доверительные интервалы для генеральной средней:

(от 6,835 до 8,365).

Задача 5.2. По данным о междугородных телефонных соединениях, предоставленных с ожиданием свыше 1 часа, определить:

- долю соединений, предоставленных с ожиданием свыше 1 часа;

- ошибку данной выборки с вероятностью ρ = 0,95.

Выборка бесповторная.

Генеральная совокупность междугородных телефонных соединений 1250 ед.

Выборочная совокупность 570 ед., в том числе с ожиданием свыше 1 часа 45 ед.

Решение

Определяется доля единиц, обладающая признаком (с ожиданием свыше 1 часа):

W = m / n W = 45 / 570 = 0,079 или 7,9 %.

Определяется предельная ошибка выборочной доли при бесповторной выборке:

, при ρ = 0,95 t = 2.

или 1,66%

Пределы доли признака в генеральной совокупности:

, т.е. в пределах от 6,56 до 9,56%.

Определяется относительная ошибка выборочной доли: %

. Относительная ошибка выборочной доли велика, значит объем выборочной совокупности недостаточен.

Задача 5.3 Сколько работников надо обследовать в порядке случайной выборки для определения средней заработной платы, чтобы с вероятностью ρ = 0,955 можно было бы гарантировать ошибку не более 50 руб., если среднее квадратическое отклонение зарплаты – 200 руб. Выборка повторная. При ρ = 0,955 t = 2.

Определить объем выборки, если ошибку выборки а) увеличить в 2 раза, в) уменьшить в 2 раза.

Решениее

Для случайного повторного отбора: ; чел.

а) если ошибку выборки увеличить в 2 раза: чел.

в) если ошибку выборки уменьшить в 2 раза: чел.

Вывод:Необходимо обследовать 64 чел. При увеличении ошибки выборки в 2 раза объем выборки уменьшается в 4 раза, при уменьшении ошибки выборки в 2 раза объем выборки увеличивается в 4 раза, т. е. происходит изменение в квадрат раз.

Типическая выборка

При определении ошибки типической выборки в случае пропорционального отбора для расчета предельной ошибки выборки применяется формула случайной выборки, в которой применяется средняя из групповых дисперсий . ∆ = t*µ

для выборки: повторной - 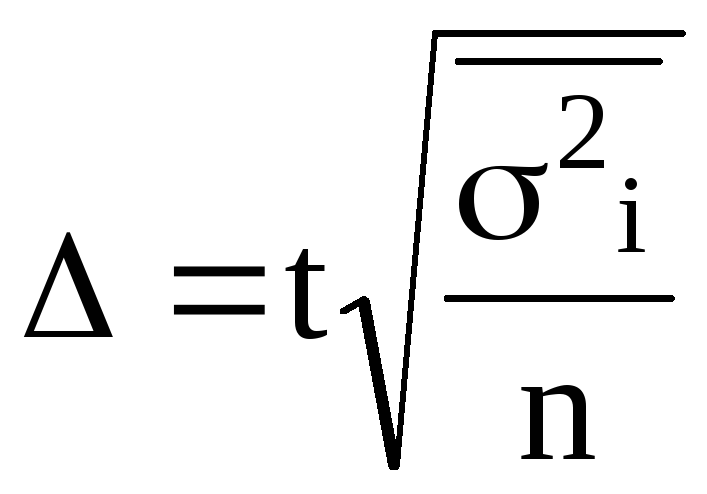; бесповторной - .

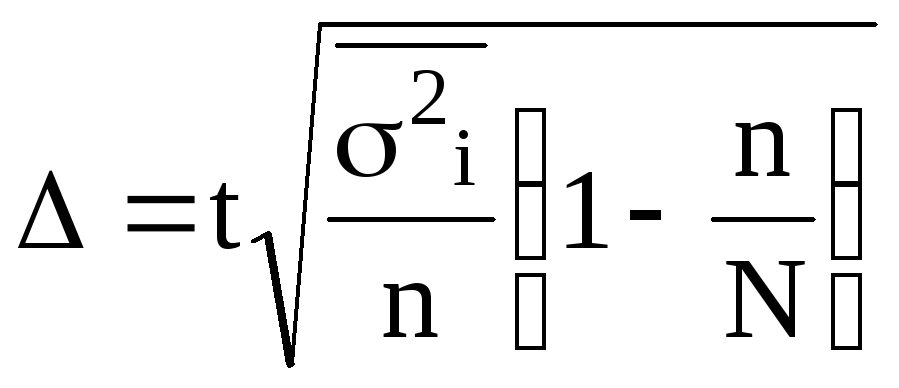Отбор единиц в типическую выборку производится пропорционально объему типических групп: ,

При определении ошибки типической выборки в случае отбора по дифференциальному признаку для расчета предельной ошибки выборки применяется формула случайной выборки, в которой применяется внутригрупповые дисперсии ²_i. ∆ = t*µ или для выборки:

повторной - 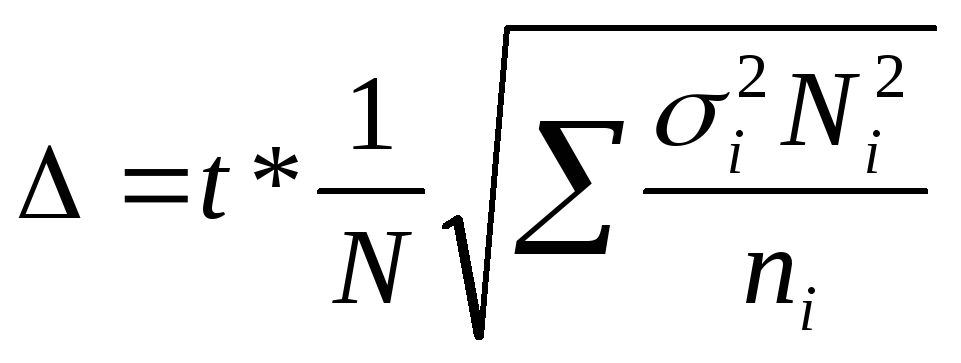; бесповторной - .

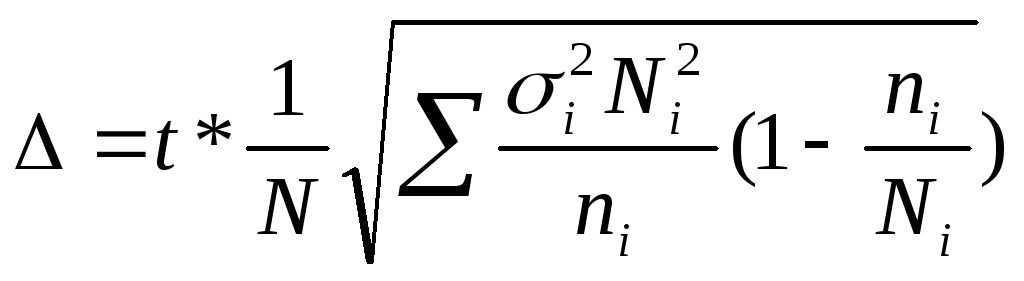Если отбор единиц в типическую выборку производится пропорционально дифференциальному признаку - среднему квадратическому отклонению , то объем типических групп определяется по формуле: .

Задача 5.4. Проведён 20% - ный повторный типический отбор переданных операторами телеграмм пропорционально объему и дифференцированному признаку. С вероятностью 0,955 определить пределы генеральной средней бракованных телеграмм. По каждому оператору имеется средняя и дисперсия бракованных телеграмм. Рассчитать относительную ошибку выборки.

Исходные данные Таблица 5.3

Операторы	Передано телеграмм, ед.	Телеграммы с браком
		средняя	дисперсия
1	2500	24	64
2	3000	32	49
3	1500	18	25

Расчетная таблица Таблица 5.4

Операторы	Передано телеграмм, единиц Ni	По телеграммам с браком получены		Обследовано пропорционально, ni
		средняя	дисперсия	oбъему	дисперсии
1	2500	24	64	500	577
2	3000	32	49	600	606
3	1500	18	25	300	217
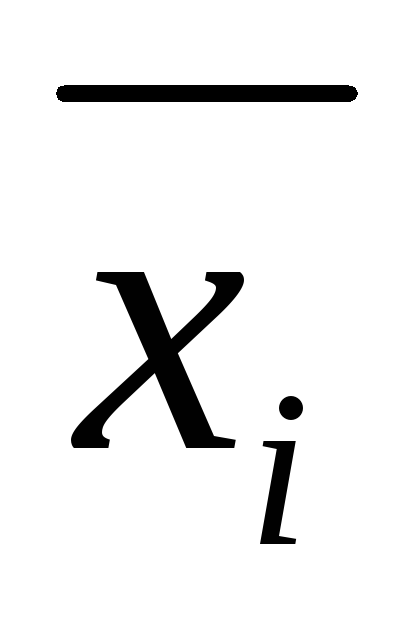
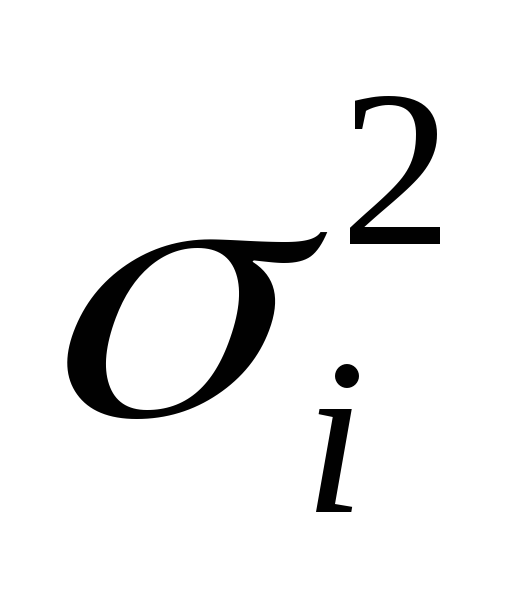
	7000 N			1400	n 1400

1. Отбор единиц в типическую выборку пропорционально объему типических групп: :

n = 0,2 * 7000 = 1400; ед.; или 0,2*2500 ед. или 0,2*3000;

ед. или 0,2*1500

2. Определяем среднюю бракованных телеграмм по всем операторам:

3. Определяем среднюю дисперсию по всем операторам:

4. Определяем предельную ошибку выборки: При р = 0,955 t = 2.

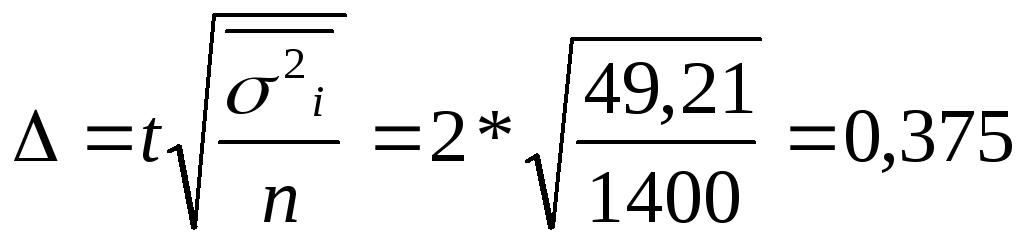
С вероятностью 95,5% можно утверждать, что среднее количество бракованных телеграмм по генеральной совокупности будет находится в пределах:

, т. е от 25,765 до 26,515 ед.

Относительная ошибка выборки при этом способе отбора составит:

.

5. Отбор единиц в типическую выборку производится пропорционально дифференцированному признаку () :

, ,

Предельная ошибка выборки будет равна:

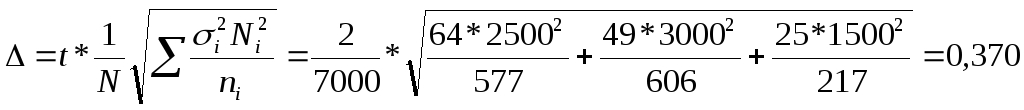
Относительная ошибка выборки при этом способе отбора составит:

.

С вероятностью 95,5% можно утверждать, что среднее количество бракованных телеграмм по генеральной совокупности будет находится в пределах:

, т. е от 25,77 до 26,51 ед.

Таким образом, отбор единиц в типическую выборку пропорционально дифференцированному признаку дает более точные результаты с меньшей и предельной и относительной ошибками выборки.

Cерийная выборка

При серийном (гнездовом) отборе в случайном порядке отбираются не единицы, а группы единиц (серии, гнезда). Серии, или группы, единиц отбираются по принципу случайного отбора или механическим способом, внутри отобранных серий (гнезд) обследованию подвергаются все единицы. Если общее число серий в генеральной совокупности обозначить через R, а число отобранных серий – r, то средняя ошибка выборки может быть определена по формулам:

_x = 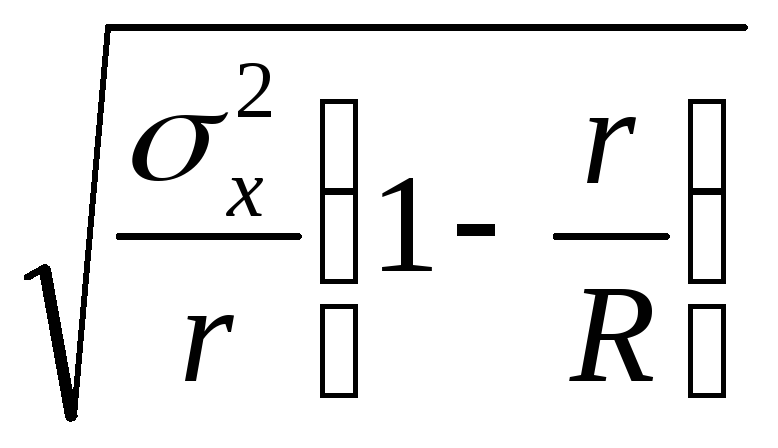для бесповторной выборки, _x = , повторной выборки,

где – межсерийная (межгрупповая) дисперсия.

Объём серийной выборки определяется по формуле: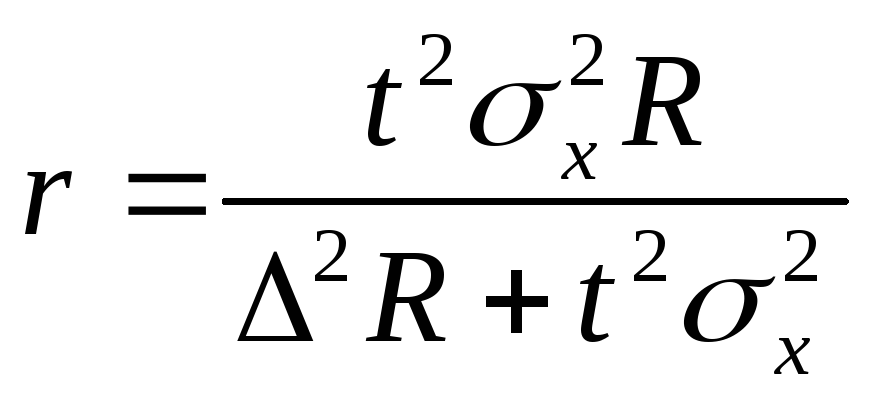

Задача 5.5. На склад фирмы поступило 100 ящиков изделий по 80 штук. Для установления среднего веса изделия следует провести серийную выборку изделий методом механического отбора так, чтобы с вероятностью р = 0,954 ошибка выборки не превышала 2 г. Из предыдущих обследований известно, что дисперсия серийной выборки равна 4. Определить необходимый объем выборки.

Объём серийной выборки определяется по формуле: .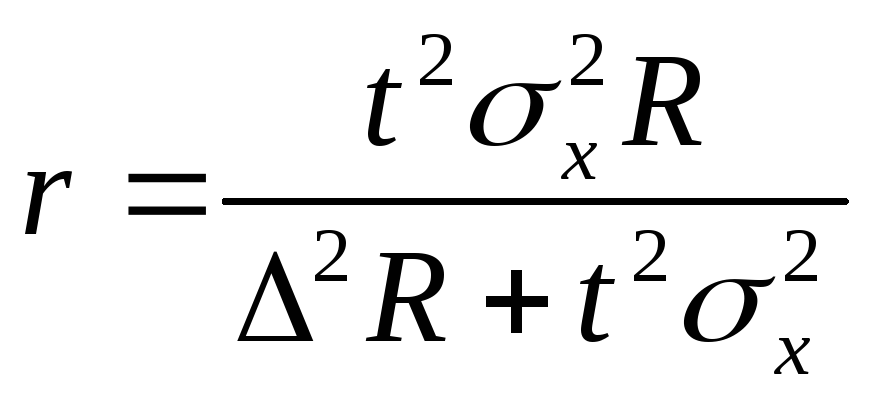

При р = 0,954 t = 2, ∆² = 2, R = 100, =4.

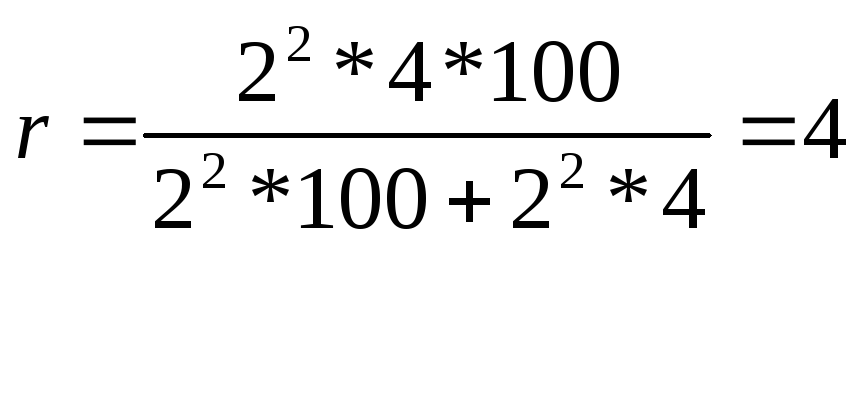ящика или 320 (4*80) изделий.

Малая выборка

Малойназывают выборку, объем которой находится в пределах 5...30 ед.

Результаты малой выборки оцениваются по закону распределения вероятностей Стьюдента.

Для определения возможных пределов ошибки пользуются так называемым критерием Стьюдента, определяемым по формуле :

,

где - мера случайных колебаний выборочной средней в малой выборке. Величина вычисляется на основе данных выборочного наблюдения:

_.

Распределение Стьюдента имеет параметр «число степеней свободы»:

На практике пользуются таблицами распределения Стьюдента S(t*), в которых для различных n и t* приведены вероятности Р(t*). В табл. 5.6 даны значения доверительной вероятности Р(t*), рассчитанные для различных t* и k (k – число степеней свободы, равное n–1).

Доверительная вероятность Р(t*) Таблица 5.6

t*	Степени свободы k
	4	5	6	7	8	9	10	15	20	
2,0 2,5 3,0	0,844 0,933 0,960	0,898 0,946 0,970	0,908 0,953 0,976	0,914 0,959 0,980	0,919 0,963 0,983	0,923 0,966 0,985	0,927 0,969 0,987	0,936 0,976 0,991	0,941 0,979 0,993	0,954 0,988 0,997

По этой таблице определяется двусторонний критерий, т.е. вероятность того, что фактическое значение t* по случайным причинам не будет больше табличного по абсолютной величине.

Средняя ошибка малой выборки рассчитывается по формуле:

_мв =или .

Предельная ошибка малой выборки равна: _мв = t*∙ _мв.

Доверительные интервалы для генеральной средней:

Задача 5.6.Определить среднюю величину срока службы 10 отобранных радиоламп и доверительные интервалы для генеральной совокупности с вероятностью 96,6 %. Сроки службы 10 отобранных радиоламп представлен в таблице 5.7.

Срок службы 10 радиоламп, час. Таблица 5.7

1	2	3	4	5	6	7	8	9	10
1450	1370	1250	1400	1360	1420	1400	1320	1300	1430

Решение

Средняя ошибка малой выборки: _мв = .

Предельная ошибка малой выборки : _мв = t*∙ _мв.

Расчетная таблица Таблица 5.8

№ п/п	1	2	3	4	5	6	7	8	9	10	∑
Срок горения	1450	1370	1250	1400	1360	1420	1400	1320	1300	1430	13700
(х-ẋ)2	6400	0	14400	900	100	2500	900	2500	4900	3600	36200

Средняя величина срока службы радиолампы:

Дисперсия выборки:

Средняя ошибка малой выборки: _мв =

Предельная ошибка малой выборки : _мв = t*∙ _мв. = 2,5*20 = 50 час.

t* = 2,5 при р = 0,966 и

Доверительные интервалы для генеральной средней: :

(от 1320 до 1420 час.).

Вывод:Средний срок службы радиолампы будет находится в пределах от 1320 до 1420 час. и разница между средней выборочной и генеральной средней не превысит 50 час. с вероятностью 96,6 %.