7. Относительные показатели вариации

Задача 3.3. По расчетным данным задач 2.3 и 3.1 (средняя величина =21,594, размах вариации = 23,9, среднее линейное отклонение = 4,429, среднее квадратическое отклонение = 5,393) рассчитать относительные показатели вариации.

1. Коэффициент осцилляции:

2. Линейный коэффициент вариации:

3. Коэффициент вариации:

Совокупность можно считать однородной, т. к.

8. Расчет асимметрии и эксцесса.

1. Асимметрия: 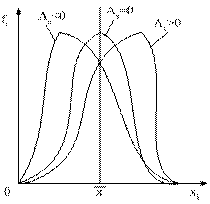а)

б)

в)

Центральный момент третьего порядка: ₃ = (m₃ – 3m₁ m₂ + 2m₁³)·i³ ₌

[(-6,6354)-3∙( -0,6354) ∙3,6354+2 ∙ (-0,6354³)] ∙3³ = -5,904

Вывод: асимметрия левосторонняя, слабосмещенная.

2. Эксцесс:

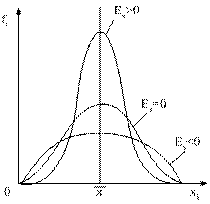
Центральный момент четвёртого порядка: ₄ = (m₄ – 4m₃ m₁ + 6m₂m₁² - 3m₁⁴)·i⁴

[33,6354 – 4*(-6,6354)*(-0,6354) + 6*3,6354*(-0,6354²) - 3*(-0,6354⁴)]*3⁴ ₌ 2032,152.

Вывод: низковершинное распределение.

9. Определения близости эмперического и теоретического распределений

Под выравниванием вариационных рядов понимается подбор теоретического распределения, близкого к фактическому (эмпирическому) распределению и определение существенности расхождения между ними с использованием критериев согласия (Колмогорова, Пирсона, Романовского).

В основу теоретического распределения положено нормальное распределение, которое описывается формулой:

,

где: Y – ордината кривой нормального распределения;

- нормальные отклонения, т.е. отклонения вариантов от , выраженные в единицах среднего квадратического отклонения σ.

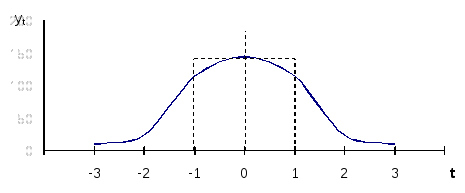
-3σ -2σ - σ + σ +2σ -3σ

Рис. 4.3 Кривая нормального распределения

При выравнивании вариационного ряда по кривой нормального распределения теоретические частоты ряда определяются по формуле:

,

где: N = ∑f - сумма всех частот вариационного ряда;

h = i – величина интервала в группах;

- постоянный множитель, характеризующий данный вариационный ряд.

Величина (значение функции) табулирована.

Задача 4.9. По имеющимся данным о количестве работников компании и их заработной плате определить эмпирическое и теоретическое распределения и определение существенности расхождения между ними с использованием критериев согласия (Колмогорова, Пирсона, Романовского).

Таблица 3.3

Расчетная таблица определения близости эмперического и теоретического распределений

Группа по зарплате тыс. руб	Численн. работников, чел.	Средняя интервала			f(t)	φ(t)	Кумулятивные частоты фактич. теоретич. ∑φ ∑f		Разность ∑f -­ ∑φ
10,1 - 13	7	11,5	-10,094	-1,87	0,0694	3,7	7	3,7	3,3
13,1 - 16	9	14,5	-7,094	-1,32	0,1669	8,9	16	12,6	D 3,4
16,1 - 19	14	17,5	-4,094	-0,76	0,2989	16,0	30	28,6	1,4
19,1 - 22	19	20,5	-1,094	-0,20	0,3910	20,9	49	49,5	-0,5
22,1 - 25	22	23,5	1,906	0,35	0,3752	20,0	71	69,5	1,5
25,1 - 28	13	26,5	4,906	0,91	0,2637	14,1	84	83,6	0,4
28,1 - 31	8	29,5	7,906	1,47	0,1354	7,2	92	90,8	1,2
31,1 - 34	4	32,5	10,906	2,02	0,0519	2,8	96	93,6	2,4
k = i = 3,0	96					93,6

продолжение таблицы

Группа по зарплате тыс. руб	Число работников fТ	fэ – fТ	(fэ – fТ)² / fТ
10,1 - 13	4	3	2,25	713,222
13,1 - 16	9	0	0	452,924
16,1 - 19	16	-2	0,25	234,652
19,1 - 22	21	-2	0,190	22,740
22,1 - 25	20	2	0,2	79,922
25,1 - 28	14	-1	0,071	312,895
28,1 - 31	7	1	0,143	500,039
31,1 - 34	3	1	0,333	475,763
	94		3,438	2792,156

Решение

1. Расчёт средней заработной платы:

2. Расчёт среднеквадратического отклонения:

.

2. Расчет теоретических частот ряда :

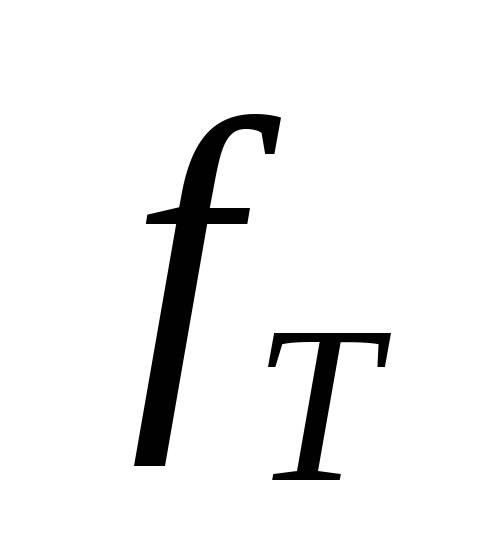2. Расчет критерия согласия.

Критерий Колмогорова ():

По таблице значений P(λ) P(λ=0,347)=0,9997

С вероятностью 99,97% можно утверждать, что расхождения между эмпирическим (фактическим) и теоретическим распределением имеют случайный характер.

находится по таблице, близко к 1,0.

Число работников
фактическое	теоретическое
7	4
9	9
14	16
19	21
22	20
13	14
8	7
4	3
96	94

Вывод: расхождения между эмпирическим и теоретическим рядами распределения не существенны и носят случайный характер.

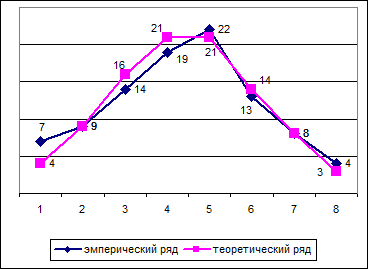
Рис. 4.4 Эмпирический и теоретический ряды распределения

Критерий Пирсона ()("хи-квадрат") :.

Условие близости эмпирического и теоретического распределений:

При v = h-3 = 8-3 = 5 и α = 0,05 .V - число степеней свободы,

h- число групп ряда, α – уровень значимости.

Если ,значит различия не существенны.

По таблице «Значения - критерия Пирсона при полученных значениях

число степеней свободы Уровень значимости принимаем α = 0,05 ; m - число групп; n - число параметров.

Критерий Романовского: .

Если C< 3, значит различия не существенны.

Правило 3-х :

Критерии согласия могут определить зону для нормального распределения эмпирического ряда распределения:

21,59 + 5,39 = 26,98 21,59 - 5,39 = 16,2;

21,59 + 2*5,39 = 32,37 21,59 - 2*5,39 = 10,81;

21,5 + 3* 5,39 = 37,76 21,5 - 3* 5,39 = 5,42.

В пределах границ находятся частоты:

от 16,20 до 26,98 (22+19) = 41 41/96 = 42,7%;

от 10,81 до 32,37 (41+14+13+) = 68 68/96 = 70,8%;

от 5,42 до 37,76 (68+7+9+8) = 92 92/96 = 95,8%.

Таким образом, большинство частот эмпирического ряда распределения (95,8%) находятся в пределах 3-х σ.