Тема 3. Показатели вариации

Цель занятия: Ознакомится с различными видами и свойствами показателей вариации, способами их расчета.

Задача 3.1. На основании исходных данных о заработной плате работников и их количестве рассчитать показатели вариации.

В расчетах используются данные, приведенные в таблице 3.1.

1. Размах вариации:

R = x_max – x_min = 34,0 - 10,1 = 23,9 тыс. руб.

2. Среднее линейное отклонение:

3. Дисперсия:

а) традиционный способ:

б) способ расчёта от «условного нуля»

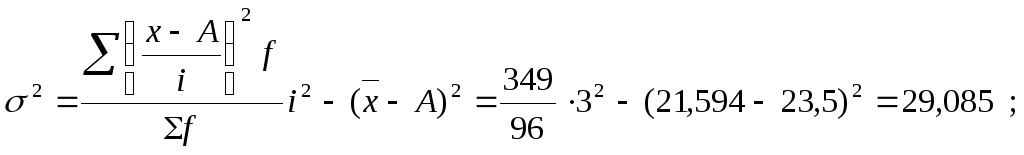
в) способ разностей между средней квадратов и квадратом средней:

г) способ моментов:

4. Условные моменты:

Расчетная таблица определения дисперсии и условных моментов Таблица 3.1

Группа по зарплате тыс. руб	Численн. работников, чел.	Средняя интервала
10,1 - 13	7	11,5	70,658	713,222	-4	-28	112	-448	1792	925,75
13,1 - 16	9	14,5	63,846	452,924	-3	-27	81	-243	729	1892,25
16,1 - 19	14	17,5	57,316	234,652	-2	-28	56	-112	224	4287,5
19,1 - 22	19	20,5	20,786	22,740	-1	-19	19	-19	19	7984,75
22,1 - 25	22	23,5	41,932	79,922	0	0	0	0	0	12149,5
25,1 - 28	13	26,5	63,778	312,895	1	13	13	13	13	9129,25
28,1 - 31	8	29,5	63,248	500,039	2	16	32	64	128	6962
31,1 - 34	4	32,5	43,624	475,763	3	12	36	108	324	4225
k = i = 3,0	96		425,188	2792,156		-61	349	-637	3229	47556,0

5. Среднее квадратическое отклонение:

6. Сложение дисперсий

Определение количественных изменений признака по группам, на которые разбита вся совокупность, а также и между группами посредством вычисления и анализа дисперсий: общей, межгрупповой, внутригрупповой и средней из внутригрупповых дисперсий.

Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловливающих эту вариацию:

.

Межгрупповая дисперсия характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки:

, где

- соответственно средние и численности по отдельным группам,

- средняя всей совокупности.

Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основу группировки:

, где

- варианты групп, - численность группы, - средняя группы

Средняя из внутригрупповых дисперсий определяется по формуле:

.

Общая дисперсия определяется как сумма средней из внутригрупповых дисперсий и межгрупповой дисперсии:

.

Данная сумма называется правилом сложения дисперсий.

Общая дисперсия, возникает под влиянием всех факторов, равна сумме дисперсий, возникающих под влиянием прочих факторов, и дисперсии, возникающей за счет группировочного признака.

Показатель тесноты связи между группировочным (факторным) и результирующим признаками называется эмпирическим корреляционным отношением и рассчитывается как корень квадратный из отношения межгрупповой дисперсии к общей дисперсии: .

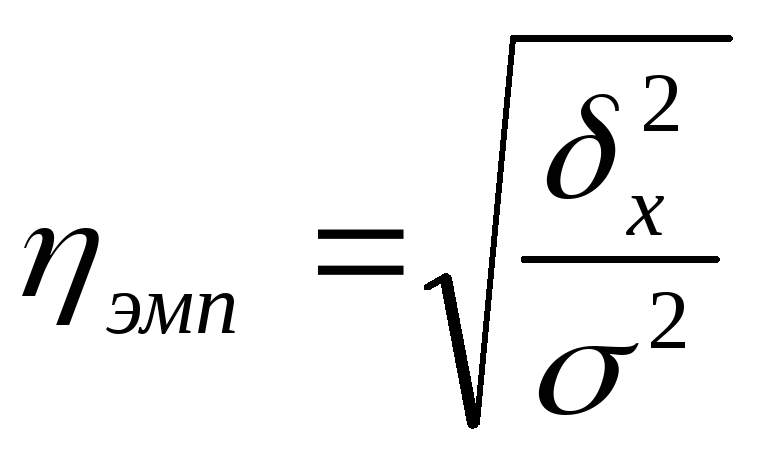Отношения межгрупповой дисперсии к общей дисперсии называется эмпирическим коэффициентом детерминации и показывает долю группировочного признака в общей вариации: .

Рассчитывается коэффициент вариации по каждой группировки и в целом по всей совокупности:

Задача 3.2. Объяснить, чем вызвана вариация производительности труда на двух предприятиях с различными группами работников. Вычислить все виды дисперсий. Определить степень влияния разряда работников на производительность труда.

Таблица 3.2

Исходные данные

Предприятия с работниками	Количество предприятий	Средняя производительность труда, тыс. руб./чел.	Среднее квадратическое отклонение
1-3 го разряда	6	200	40
4-6 го разряда	4	400	30

1. Внутригрупповая дисперсия: 40² = 1600 ; 30² = 900.

2. Межгрупповая дисперсия: = .

3. Средняя межгрупповая: .

4. Средняя из внутригрупповых дисперсий:

5. Правило сложения дисперсий: общая дисперсия : .

6. Эмпирический коэффициент детерминации: .

Вывод: Группировочным признаком обусловлено 87,9% вариации производительности труда от разряда квалификации.

7. Эмпирическое корреляционное отношение: =

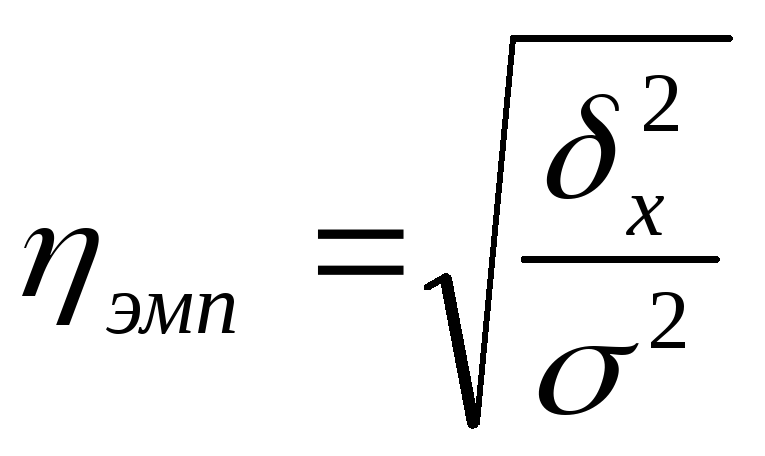Связь между производительностью труда и разрядом квалификации сильная.

8. Коэффициент вариации по первой группировке:

коэффициент вариации по второй группировке:

общий коэффициент вариации

в целом по всей совокупности:

Совокупность каждой группировки можно считать однородной, так как коэффициенты вариации меньше 33%. Общая совокупность не однородная, так как коэффициент вариации больше 33%.