
- •Статистика общая теория
- •1. Представление вариационного ряда в виде таблицы:
- •2. Представление вариационного ряда в виде полигона:
- •1. Определение размера и количества интервалов
- •2. Построение вариационного ряда с интервалом 3,0 тыс. Руб.
- •3. Представление вариационного ряда в виде таблицы:
- •Тема 2. Средние величины.
- •2.1 Степенные средние
- •2.2 Структурные средние
- •Тема 3. Показатели вариации
- •1. Размах вариации:
- •2. Среднее линейное отклонение:
- •3. Дисперсия:
- •5. Среднее квадратическое отклонение:
- •6. Сложение дисперсий
- •7. Относительные показатели вариации
- •8. Расчет асимметрии и эксцесса.
- •9. Определения близости эмперического и теоретического распределений
- •Тема 4 Абсолютные и относительные величины
- •Тема 5. Выборочное наблюдение
- •Тема 6 . Статистические методы изучения взаимосвязи между явлениями. Корреляционно-регрессионный анализ.
- •6.1. Парная корреляция
- •6.2 Корреляционно-регрессионный анализ для многофакторной модели.
- •Тема 7 Ряды динамики
- •Тема 8. Индексный метод
- •8.2 Среднеарифметический и среднегармонический индексы.
- •8.3. Индексы качественных показателей.
- •Список литературы
Тема 2. Средние величины.
Цель занятия: Ознакомится с различными видами средних (степенными, структурными), их свойствами и способами расчёта.
2.1 Степенные средние
Степенные средние: простая
![]() ,
взвешенная
,
взвешенная
![]() ,
,
где х – варианта, т.е. варьирующая, изменяющаяся величина признака; n – число единиц или объем совокупности (число вариантов); f – частота признака (вес I-того варианта); z – показатель степени средней.
Таблица 2.1
Виды степенных средних и формулы их расчёта
|
Наименование средней |
Условное обозначение |
Значение степени |
Формула средней | |
|
простой |
взвешенной | |||
|
средняя гармоническая |
|
–1 |
|
|
|
средняя геометрическая |
|
0 |
|
|
|
средняя арифметическая |
|
+1 |
|
|
|
средняя квадратическая |
|
+2 |
|
|
«правило
мажорантности средних»:
![]() <
<![]() <
<![]() <
<![]()
Задача 2.1. На основании исходных данных рассчитать средние и показать «правило мажорантности средних».
-
54
62
68
74
80
86
Расчетная таблица средних Таблица 2.2
|
|
|
|
|
|
|
|
∑ |
|
x |
54 |
62 |
68 |
74 |
80 |
86 |
424 |
|
1/x |
0,0185 |
0,0161 |
0,0147 |
0,0135 |
0,0125 |
0,0116 |
0,0870 |
|
х² |
2916 |
3844 |
4624 |
5476 |
6400 |
7396 |
30656 |
средняя
гармоническая:
![]() ;
;
средняя
геометрическая:
![]() ;
;
средняя
арифметическая:
![]() ;
;
средняя
квадратическая:
![]() .
.
«правило мажорантности средних»:
![]() <
<
![]() <
<![]() <
<![]() 68,97 < 69,83 < 70,67 < 71,48
68,97 < 69,83 < 70,67 < 71,48
Вывод: Величина степенных средних зависит от их степени, наибольшее значение имеет
средняя квадратическая (значение степени равно +2).
Задача 2.2. По приведенным данным вычислить среднюю доходную таксу по письменной корреспонденции в целом по группе РУС за 1-е и 2-е полугодие, а также за год.
Исходные данные Таблица 2.3
-
РУС
1-е полугодие
2-е полугодие
средняя доходная
такса, руб.
количество
писем, тыс.ед.
средняя доходная
такса, руб.
Сумма доходов
тыс. руб.
1
23,4
1250
28,6
31317,0
2
28,6
780
32,7
26977,5
3
21,9
950
25,2
28904,4
4
24,2
1170
29,3
27776,4
Решение
Расчетная таблица Таблица 2.4
|
РУС |
1-е полугодие |
2-е полугодие |
Х1*f1
|
(М/Х2)
| ||
|
|
средняя доходная. такса Х1 |
количество писем f1 |
средняя доходная. такса . Х2 |
сумма доходов тыс. руб. М | ||
|
| ||||||
|
|
| |||||
|
1 |
23,4 |
1250 |
28,6 |
31317,0 |
29250 |
1095 |
|
2 |
28,6 |
780 |
32,7 |
26977,5 |
22308 |
825 |
|
3 |
21,9 |
950 |
25,2 |
28904,4 |
20805 |
1147 |
|
4 |
24,2 |
1170 |
29,3 |
27776,4 |
28314 |
948 |
|
∑ |
|
4150 |
|
114975,3 |
100677 |
4015 |
|
1-е
полугодие используется
среднеарифметическая:
2-е
полугодие используется
среднегармоническая:
За
год:
| ||||||
Задача 2.3. На основании исходных данных о заработной плате работников и их количестве рассчитать среднюю величину вариационного ряда с помощью способа "от условного нуля" и традиционным способом.
Таблица 2.5
Исходные данные
|
Группа по зарплате тыс. руб. |
10,1 - 13 |
13,1 - 16 |
16,1 - 19 |
16,1 - 19 |
22,1 - 25 |
25,1 - 28 |
28,1 - 31 |
31,1 - 34 |
|
Количество работников, чел. |
7 |
9 |
14 |
19 |
22 |
13 |
8 |
4 |
Таблица 2.6
Расчетная таблица средней
-
Группа по зарплате
тыс. руб.
Количество
работников, чел.
Средняя интервала
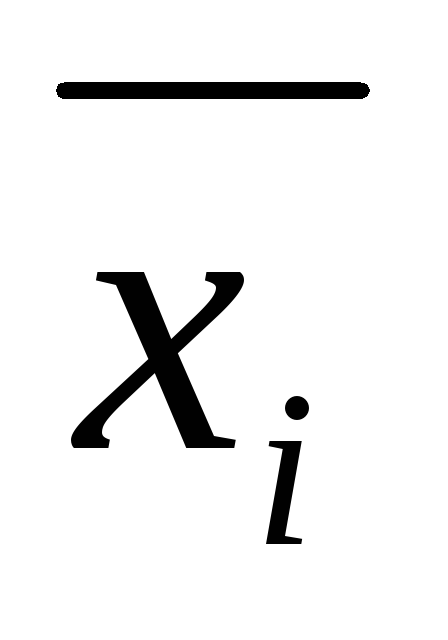
x∙f
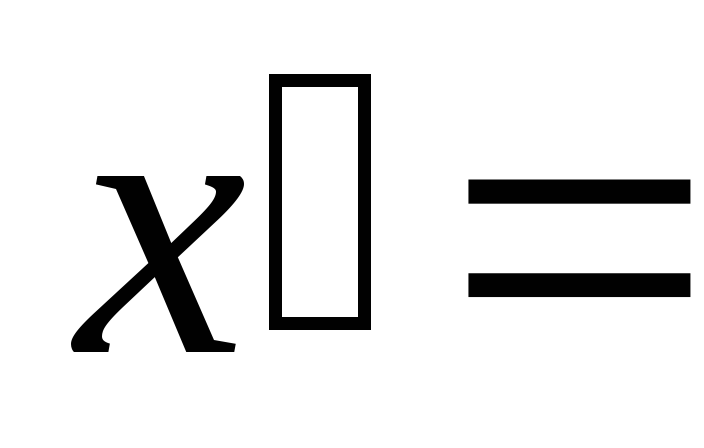
(x-A) / i
A=23,5
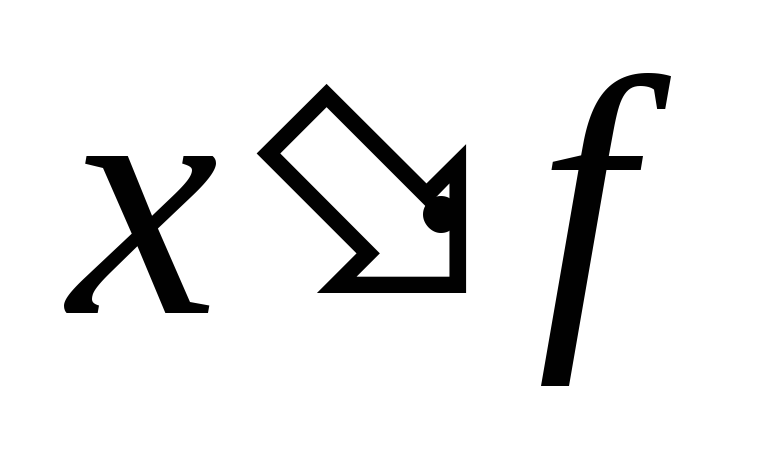
10,1 - 13
7
11,5
80,5
-4
-28
13,1 - 16
9
14,5
130,5
-3
-27
16,1 - 19
14
17,5
245
-2
-28
19,1 - 22
19
20,5
389,5
-1
-19
22,1 - 25
22
23,5
517
0
0
25,1 - 28
13
26,5
344,5
1
13
28,1 - 31
8
29,5
236
2
16
31,1 - 34
4
32,5
130
3
12
k = i = 3,0
96
2073
-61
Расчёт средней способом "от условного нуля":
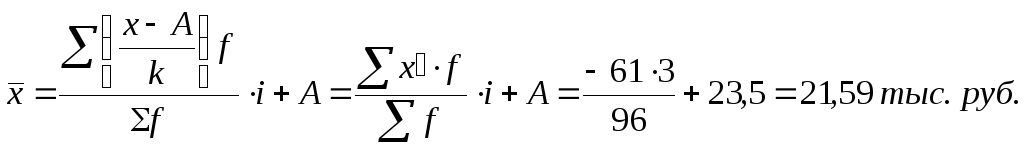
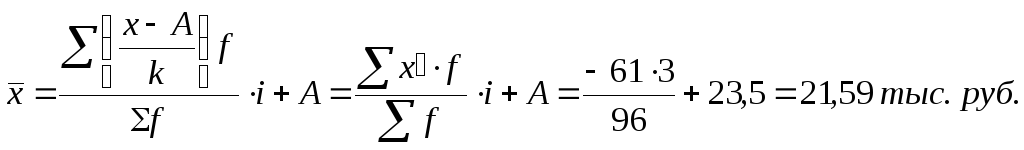
Расчёт средней традиционным способом по формуле среднеарифметической взвешанной:
![]()
Задача 2.4 На основании исходных данных о количестве работников определить среднее ежегодное изменение работников в %.
Таблица 2.7
Исходные данные
|
Показатели |
2005 |
2006 |
2007 |
2008 |
2009 |
|
Численность работников |
2327 |
2506 |
1999 |
1929 |
1263 |
Таблица 2.8
Расчетная таблица
|
|
2005 |
2006 |
2007 |
2008 |
2009 |
|
Численность работников |
2327 |
2506 |
1999 |
1929 |
1263 |
|
Цепные индексы роста работников |
1 |
1,077 |
0,798 |
0,965 |
0,655 |
Используется
средняя геометрическая:
![]()
4 ____________________________
√1,077*0,798*0,965*0,655 = 0,8585 = 85,85%

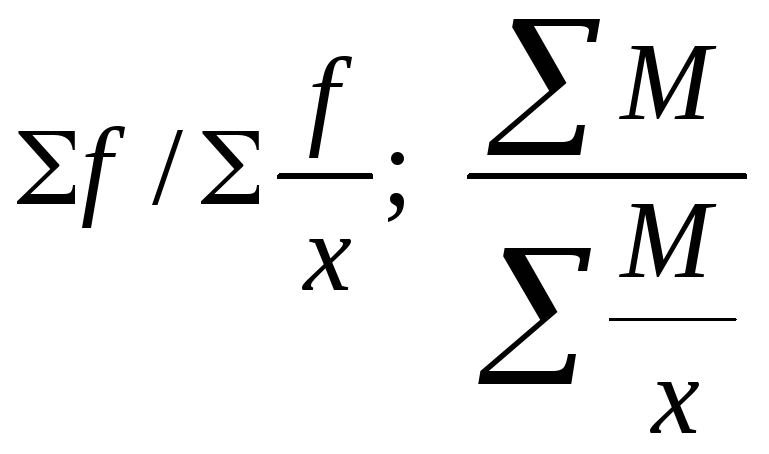
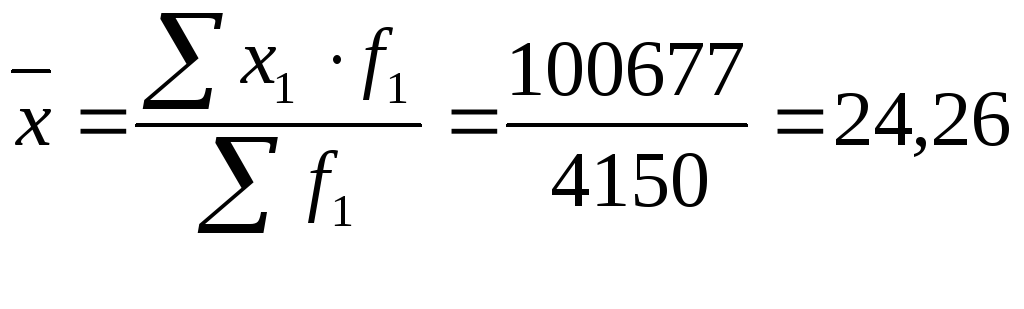 руб.
руб.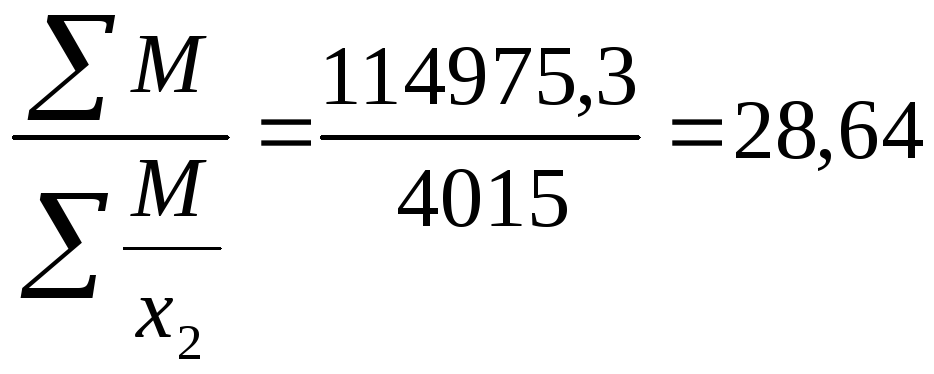 руб.
руб.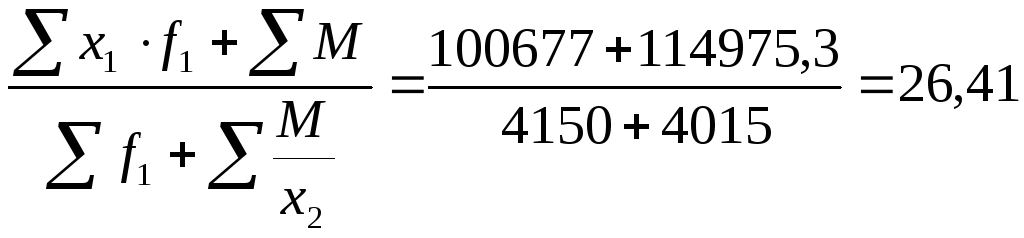 руб.
руб.