
- •Статистика общая теория
- •1. Представление вариационного ряда в виде таблицы:
- •2. Представление вариационного ряда в виде полигона:
- •1. Определение размера и количества интервалов
- •2. Построение вариационного ряда с интервалом 3,0 тыс. Руб.
- •3. Представление вариационного ряда в виде таблицы:
- •Тема 2. Средние величины.
- •2.1 Степенные средние
- •2.2 Структурные средние
- •Тема 3. Показатели вариации
- •1. Размах вариации:
- •2. Среднее линейное отклонение:
- •3. Дисперсия:
- •5. Среднее квадратическое отклонение:
- •6. Сложение дисперсий
- •7. Относительные показатели вариации
- •8. Расчет асимметрии и эксцесса.
- •9. Определения близости эмперического и теоретического распределений
- •Тема 4 Абсолютные и относительные величины
- •Тема 5. Выборочное наблюдение
- •Тема 6 . Статистические методы изучения взаимосвязи между явлениями. Корреляционно-регрессионный анализ.
- •6.1. Парная корреляция
- •6.2 Корреляционно-регрессионный анализ для многофакторной модели.
- •Тема 7 Ряды динамики
- •Тема 8. Индексный метод
- •8.2 Среднеарифметический и среднегармонический индексы.
- •8.3. Индексы качественных показателей.
- •Список литературы
Тема 7 Ряды динамики
Цель занятия: Ознакомится с различными видами рядов динамики.
Темпы
роста:
цепной
![]() ,
базисный
,
базисный
![]() ,
,
![]()
Приросты:
цепные
![]() ,
,
![]()
базисные
![]() ,
,
![]()
Абсолютное значение одного
процента прироста:
![]()
Среднегодовой
темп роста:
![]() или
или
![]() ,
,
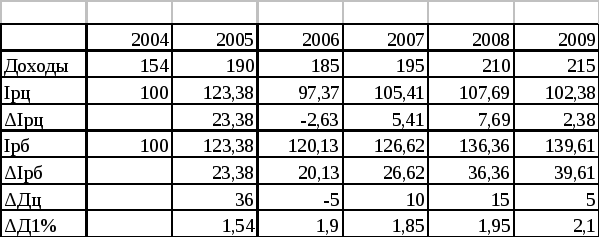
Задача 7.1 По данным о доходах за 2004-2009 годы рассчитать темпы роста, прироста базисные и цепные; абсолютный прирост 1 % прироста, среднегодовой рост и прирост доходов за расчётный период.
Исходные данные
Таблица 6.1
-
Период
2004
2005
2006
2007
2008
2009
Доходы млн. руб.
154
190
185
195
210
215
Решение:
Расчетная таблица Таблица 7.2
![]()
Среднегодовой рост и
прирост доходов за расчётный период
определяем, используя формулу средней
геометрической: ![]()
![]()
![]()
Среднегодовой рост доходов составляет: 106,9 %;
Среднегодовой прирост доходов составляет: 106,9 – 100 = 6,9 %.
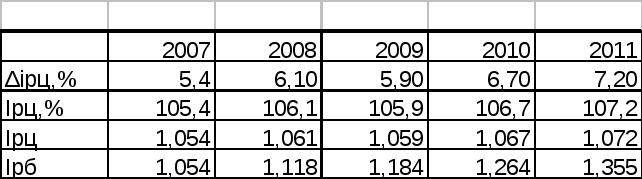
Задача 7.2 По данным о ежегодных темпа прироста междугородных телефонных соединений за 2005-2009 вычислить среднегодовой темп роста и прироста за весь период.
Исходные данные Таблица 6.3
|
|
2007 |
2008 |
2009 |
2010 |
2011 |
|
Темпы прироста междугородных телефонных соединений, % |
5,4 |
6,10 |
5,90 |
6,70 |
7,20 |
Решение
Расчетная таблица Таблица 7.4
Среднегодовой темп роста:
![]() ,
прироста:
,
прироста:
![]()
![]() или
106,3%.
или
106,3%.
Среднегодовой темп прироста:
![]()
![]()
Задача 7.3 Провести смыкание рядов динамики по данным об объёме продукции за 2003 - 2009 годы по двум периодам: за 2003 - 2005 г.г. и 2005 - 2009 г.г. в относительном и абсолютном выражении.
Исходные данные Таблица 6.5
|
Период |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
|
Объём продукции, млн. руб. в старых условиях |
349
|
453
|
560
|
|
|
|
|
|
в новых условиях |
|
|
648 |
685 |
735 |
795 |
846 |
Решение
Расчетная таблица Таблица 6.6
|
Период |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
|
Объём продукции, млн. руб. в старых условиях |
349
|
453
|
560
|
|
|
|
|
|
в новых условиях |
|
|
648 |
685 |
735 |
795 |
846 |
|
млн. руб. |
403,8 |
524,1 |
648 |
685 |
735 |
795 |
846 |
|
%
|
62,3 |
80,9 |
100 |
105,7 |
113,4 |
122,7 |
130,6 |
Год, в котором начинают действовать новые условия и имеются данные, как в старых, так и в новых условиях, называется годом смыкания. В данной задаче – это 2005 год.
Определяем коэффициент смыкания: Ксмык = 648/560 = 1,157
Для определения объёма продукции в новых условиях за 2003 и 2004 годы умножаем их значения в денежных единицах на коэффициент смыкания. Например, за 2003 год объём продукции в новых условиях равен 403,8 ( 349*1,157) млн. руб.
Для определения объёма продукции в новых условиях за весь период в процентах год смыкания принимаем за 100 %.
Объём продукции в новых условиях за 2003 г. будет равен 62,3 (349*100/560) % и т. д.
Объём продукции в новых условиях за 2006 г. будет равен 105,7 (685*100/648) % и т. д.
Задача 7.4 Провести выравнивание нагрузки с использованием 3-х и 5- ти месячных скользящих, рассчитать коэффициенты неравномерности нагрузки.
Исходные данные и расчет скользящих Таблица 6.7
|
Месяц |
Нагрузка |
скользящая 3-х мес |
скользящая 5-ти мес |
Кнеравн | ||
|
|
тыс. ед. |
сумма |
средняя |
сумма |
средняя |
% |
|
1 |
511 |
|
|
|
|
107,3 |
|
2 |
461 |
1461 |
487 |
|
|
96,8 |
|
3 |
489 |
1407 |
469 |
2368 |
474 |
102,7 |
|
4 |
457 |
1396 |
465 |
2318 |
464 |
95,9 |
|
5 |
450 |
1368 |
456 |
2316 |
463 |
94,5 |
|
6 |
461 |
1370 |
457 |
2267 |
453 |
96,8 |
|
7 |
459 |
1360 |
453 |
2266 |
453 |
96,4 |
|
8 |
440 |
1355 |
452 |
2288 |
458 |
92,4 |
|
9 |
456 |
1368 |
456 |
2366 |
473 |
95,7 |
|
10 |
472 |
1467 |
489 |
2427 |
485 |
99,1 |
|
11 |
539 |
1531 |
510 |
|
|
113,2 |
|
12 |
520 |
|
|
|
|
109,2 |
|
Всего |
5715 |
|
|
|
|
|
Расчет скользящих проводится в следующей последовательности:
скользящая 3-х мес сумма 511+461+489 = 1461, средняя 1461/3 = 487
сумма 461+489 + 457 = 1407, средняя 1407/3 = 469 и т. д.
скользящая 5-ти мес сумма 511+461+489 + 457 + 450 = 2368, средняя 2368/5 = 474
сумма 461 + 489+457+450 + 461=2318, средняя 2318/5 = 464 и т. д.
с![]()
![]() реднемесячная
нагрузка:
реднемесячная
нагрузка:![]() 5715/12 = 476,3.
5715/12 = 476,3.
Коэффициенты неравномерности
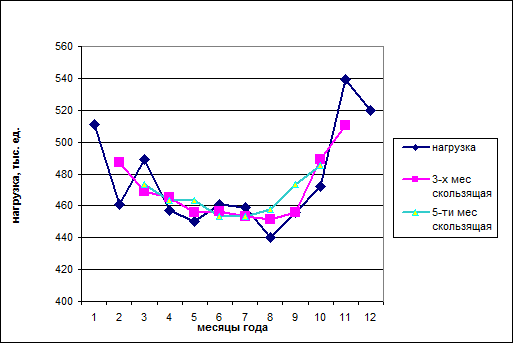
Рис. 6.1 Выравнивание нагрузки с использованием 3-х и 5- ти месячных скользящих.
Задача 7.5 По данным о доходах за 2005-2010 годы произвести выравнивание динамического ряда и спрогнозировать величину доходов на 2012 год.
Исходные данные Таблица 7.8
-
год
Доходы, млн. руб.
2005
549,3
2006
764,2
2007
1228,4
2008
2021,7
2009
2975,3
2010
3839,8
2011
4753,1
Решение
Произведем выравнивание динамического ряда по уравнению прямой: y = a0 + a1*t .
Расчетная таблица Таблица 7.9
|
год |
y |
t |
t² |
Y*t |
ỹt |
(У-ỹt)2 |
|
2005 |
549,3 |
-3 |
9 |
-1647,9 |
107,10 |
195540,8 |
|
2006 |
764,2 |
-2 |
4 |
-1528,4 |
839,58 |
5682,14 |
|
2007 |
1228,4 |
-1 |
1 |
-1228,4 |
1572,06 |
118102,2 |
|
2008 |
2021,7 |
0 |
0 |
0 |
2304,54 |
79998,47 |
|
2009 |
2975,3 |
1 |
1 |
2975,3 |
3037,02 |
3809,36 |
|
2010 |
3839,8 |
2 |
4 |
7679,6 |
3769,50 |
4942,09 |
|
2011 |
4753,1 |
3 |
9 |
14259,3 |
4501,98 |
63061,25 |
|
∑ |
16131,8 |
0 |
28 |
20509,5 |
16131,78 |
471136,3 |
Уравнение прямой: y = a0 + a1*t. a0 = ∑y/n = 16131,8/7 = 2304,54;
a1 = ∑yt/∑t² = 20509,5/28 = 732,48. ỹt = 2304,54 + 732,48*t
![]() =
259,43;
=
259,43;
![]() =259,43*100/2304,54 = 11,26 %.
=259,43*100/2304,54 = 11,26 %.
Уравнение регрессии можно использовать в целях прогнозирования, т.к. v ‹ 33%
ỹ(2012) = 2304,54+732,48*4 = 5234,46 млн. руб.
Величина доверительного интервала.
![]()
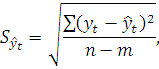
где: α – коэффициент доверия (обычно выбирается 0,05);
tα – находится по таблице «t- критерия Стьюдента» (зависит от α и числа степеней свободы v = n – m =7-2=5). tα = 2,5706
n - число уровней ряда (в примере n =7);
m - число параметров уравнения (для уравнения прямой m=2).
SYt - среднее квадратическое отклонение от тренда.
![]()
![]()
ỹ(2012) = 5234,46 ± 298,24 Доверительный интервал: min 4936,21 max 5532,69 млн. руб.
Величина относительной ошибки: S*100/ŷt %. 306,96*100/2304,54 = 13,32%.
Задача 7.6. Провести выравнивание нагрузки предприятия связи по прямой и по ряду Фурье. Определить функцию, наиболее адекватно отражающую колеблемость уровней изучаемого ряда.
Выравнивание по прямой
У![]() равнение
прямой: , где
равнение
прямой: , где
![]()
![]() 5715/12 = 476,25;
645/572 = 1,1276
5715/12 = 476,25;
645/572 = 1,1276
![]()
![]()
Показатель вариации: 28,95*100/476,25 = 6,08 %
![]()
![]()
Расчетная таблица Таблица 7.10
|
месяц
|
Письменная корреспонд. тыс. ед. У |
tпр
|
t²
|
yt
|
|
|
|
1 |
511 |
-11 |
121 |
-5621 |
463,85 |
2223,46 |
|
2 |
461 |
-9 |
81 |
-4149 |
466,10 |
26,03 |
|
3 |
489 |
-7 |
49 |
-3423 |
468,36 |
426,14 |
|
4 |
457 |
-5 |
25 |
-2285 |
470,61 |
185,29 |
|
5 |
450 |
-3 |
9 |
-1350 |
472,87 |
522,91 |
|
6 |
461 |
-1 |
1 |
-461 |
475,12 |
199,44 |
|
7 |
459 |
1 |
1 |
459 |
477,38 |
337,74 |
|
8 |
440 |
3 |
9 |
1320 |
479,63 |
1570,76 |
|
9 |
456 |
5 |
25 |
2280 |
481,89 |
670,19 |
|
10 |
472 |
7 |
49 |
3304 |
484,14 |
147,46 |
|
11 |
539 |
9 |
81 |
4851 |
486,40 |
2766,93 |
|
12 |
520 |
11 |
121 |
5720 |
488,65 |
982,60 |
|
Σ |
5715 |
0 |
572 |
645 |
5715,00 |
10058,93 |
Выравнивание по ряду Фурье
У![]() равнение:
( по одной
синусоиде), где
равнение:
( по одной
синусоиде), где
![]()
5715/12 = 476,25;
![]()
![]() 2/12 * 182,28 = 30,380;
2/12 * (-82,5) = -13,750
2/12 * 182,28 = 30,380;
2/12 * (-82,5) = -13,750
![]()
![]()
Показатель вариации: 18,52*100/476,25 = 3,89 %
![]()
![]()
Расчетная таблица Таблица 7.11
|
месяц
|
Письменная корреспонд. тыс. ед. У |
tф |
сos t |
sin t |
y*сos t |
y*sin t |
|
|
|
1 |
511 |
0 |
1 |
0 |
511 |
0,00 |
506,63 |
19,10 |
|
2 |
461 |
|
0,866 |
0,5 |
399,23 |
230,50 |
495,68 |
1202,99 |
|
3 |
489 |
|
0,5 |
0,866 |
244,50 |
423,47 |
479,53 |
89,63 |
|
4 |
457 |
|
0 |
1 |
0 |
457,00 |
462,50 |
30,25 |
|
5 |
450 |
|
-0,5 |
0,866 |
-225 |
389,70 |
449,15 |
0,72 |
|
6 |
461 |
|
-0,866 |
0,5 |
-399,23 |
230,50 |
443,07 |
321,63 |
|
7 |
459 |
|
-1 |
0 |
-459 |
0,00 |
445,87 |
172,40 |
|
8 |
440 |
|
-0,866 |
-0,5 |
-381,04 |
-220,00 |
456,82 |
282,78 |
|
9 |
456 |
|
-0,5 |
-0,866 |
-228 |
-394,90 |
472,97 |
287,90 |
|
10 |
472
|
|
0
|
-1
|
0
|
-472,00
|
490,0
|
324,00
|
|
11 |
539 |
|
0,5 |
-0,866 |
269,50 |
-466,77 |
503,35 |
1271,10 |
|
12 |
520 |
|
0,866 |
-0,5 |
450,32 |
-260,00 |
509,43 |
111,64 |
|
Σ |
5715 |
|
|
|
182,28 |
-82,50 |
5715,00 |
4114,12 |
Расчет индексов сезонности по фактическим данным, по прямой и по ряду Фурье
![]()
![]()
Индексы сезонности, % по факту: Индексы сезонности, % по прямой:
![]()
Индексы сезонности, % по Фурье:
![]()
![]() Средний индекс сезонности
показывают
по фактическим данным колеблемость
исследуемого показателя, обусловленную
сезонным спросом; по выравненным данным
отражает также сезонные колебания.
Средний индекс сезонности
показывают
по фактическим данным колеблемость
исследуемого показателя, обусловленную
сезонным спросом; по выравненным данным
отражает также сезонные колебания.
![]()
Наилучшее с точки зрения отражения сезонных колебаний нагрузки уравнение выбирают по минимуму среднего квадратического отклонения индексов сезонности от 100 %:
![]()
![]()
по факту: по прямой:
![]() по Фурье:
по Фурье:
|
Месяцы
|
У
факт |
Индексы сезонности, %
|
Отклонение от 100 %
| ||||
|
по факту |
по прямой |
по Фурье |
по факту |
по прямой |
по Фурье | ||
|
1 |
511 |
107,30 |
110,17 |
100,86 |
53,24 |
103,34 |
0,74 |
|
2 |
461 |
96,80 |
98,91 |
93,00 |
10,25 |
1,20 |
48,96 |
|
3 |
489 |
102,68 |
104,41 |
101,97 |
7,17 |
19,43 |
3,90 |
|
4 |
457 |
95,96 |
97,11 |
98,81 |
16,34 |
8,37 |
1,41 |
|
5 |
450 |
94,49 |
95,16 |
100,19 |
30,38 |
23,39 |
0,04 |
|
6 |
461 |
96,80 |
97,03 |
104,05 |
10,25 |
8,83 |
16,38 |
|
7 |
459 |
96,38 |
96,15 |
102,94 |
13,12 |
14,82 |
8,67 |
|
8 |
440 |
92,39 |
91,74 |
96,32 |
57,94 |
68,28 |
13,55 |
|
9 |
456 |
95,75 |
94,63 |
96,41 |
18,08 |
28,86 |
12,87 |
|
10 |
472 |
99,11 |
97,49 |
96,33 |
0,80 |
6,29 |
13,49 |
|
11 |
539 |
113,18 |
110,81 |
107,08 |
173,60 |
116,95 |
50,17 |
|
12 |
520 |
109,19 |
106,41 |
102,07 |
84,39 |
41,15 |
4,30 |
|
Σ |
5715 |
1200,00 |
1200,01 |
1200,05 |
475,55 |
440,91 |
174,50 |
Вывод:Расчеты показывают, что ряд Фурье наиболее адекватно отражают колеблемость уровней изучаемого ряда, так как показатели вариации и среднего квадратического отклонения индексов сезонности от 100 % имеют меньшее значение.
Прогнозирование объема письменной корреспонденции
Величина доверительного интервала определяется по формулам:
![]()
Используем для примера уравнение прямой:
![]()
![]()
α – коэффициент доверия (обычно выбирается 0,05); n - число уровней ряда;
m - число параметров уравнения (для уравнения прямой m=2)
tα – находится по таблице t критерия Стьюдента (зависит от α и числа степеней свободы
v = n – m). v = n-m = 12-2 = 10, ta = 2,2281.
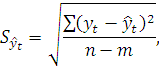
![]()
Прогноз нагрузки на 1-й месяц следующего года с учетом сезонных колебаний и доверительного интервала:
![]()
![]() (476,25 + 1,1276 * 13)*1,073 ± 20,40 = 526,745 ±
20,40, т. е.
(476,25 + 1,1276 * 13)*1,073 ± 20,40 = 526,745 ±
20,40, т. е.
С вероятностью ± 95 % можно утверждать, что величина прогнозируемого показателя на 1-й месяц следующего года будет находиться в пределах 506,345 - 547,145 тыс. ед.
Автокорреляция в рядах динамики
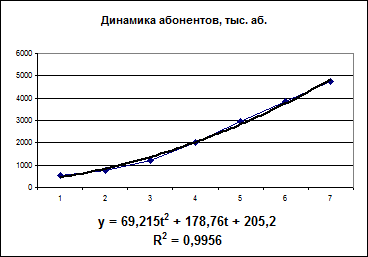
Задача 7.7. Имеются данные о количестве абонентов ГТС за 7 лет. Найти уравнение тренда, определить количество абонентов на 2010 год. Проверить полученное уравнение на наличие автокорреляции.
Таблица 7.13
-
Период
Количестве абонентов ГТС
2003
549,3
2004
764,2
2005
1228,4
2006
2021,7
2007
2975,3
2008
3839,8
2009
4753,1
Решение :
1. Определяем уравнение тренда по диаграмме, построенной в электронной таблице.
2. Рассчитываем ряд выравненных по уравнению показателей ỹt.
Расчетная таблица Таблица 7.14
|
год |
t |
y |
ỹt |
У-ỹt = ε t |
ε t-1 |
ε t*ε t-1 |
εt2 |
ε t-ε t-1 |
(ε t-ε t-1)2 |
|
2003 |
1 |
549,3 |
453,17 |
96,13 |
|
|
9240,016 |
|
|
|
2004 |
2 |
764,2 |
839,58 |
-75,38 |
96,13 |
-7245,90 |
5682,144 |
-171,51 |
29413,97 |
|
2005 |
3 |
1228,4 |
1364,42 |
-136,02 |
-75,38 |
10252,81 |
18500,08 |
-60,64 |
3676,60 |
|
2006 |
4 |
2021,7 |
2027,68 |
-5,98 |
-136,02 |
813,37 |
35,7604 |
130,04 |
16909,1 |
|
2007 |
5 |
2975,3 |
2829,37 |
145,93 |
-5,98 |
-872,63 |
21294,11 |
151,91 |
23075,13 |
|
2008 |
6 |
3839,8 |
3769,5 |
70,30 |
145,93 |
10258,53 |
4942,09 |
-75,63 |
5719,14 |
|
2009 |
7 |
4753,1 |
4848,06 |
-94,95 |
70,30 |
-6675,33 |
9016,452 |
-165,25 |
27309,22 |
|
∑ |
|
16131,8 |
16131,78 |
0,02 |
|
6530,84 |
68710,65 |
|
106103,2 |
3. Определяем остаточные величины У-ỹt = ε t и проверяем их на наличие
автокорреляции по коэффициенту автокорреляции (ra):
ra = ∑ ε t*ε t-1 / ∑ εt2 = 6530,84/68710,65 = 0,095.
Если ra = 0, то автокорреляция отсутствует. Если ra не равна 0, то автокорреляцию проверяют по критерию Дурбина - Ватсона (d ).
4. Проверяем остаточные величины У-ỹt = ε t на наличие автокорреляции по критерию
Дурбина - Ватсона (d ).
Рассчитывается величина ( d ) и сравнивается по таблице со значениями d1 и d2.
d = (ε t-ε t-1)2 / ∑ εt2 = 106103,15/68710,65 = 1,544
По таблице значений критерия Дурбина – Ватсона при 5% - ном уровне существенности определяем d1 и d2. При ν =1 ( число переменных) и n (число наблюдений) =7 <15
d1 = 1,08 d2 = 1,36 d > d2 1,544 > 1,36
Следовательно, автокорреляция отсутствует. Уравнение можно использовать для прогнозирования количества абонентов на 2010 год.
ỹt= 69,215*8²+178,76*8+205
Статистический анализ структуры. Показатели структуры и структурных сдвигов.
Для статистической оценки структурных сдвигов рассчитываются две группы показателей:
показатели, основывающиеся на абсолютной разности между удельными весами одноименных частей совокупности:
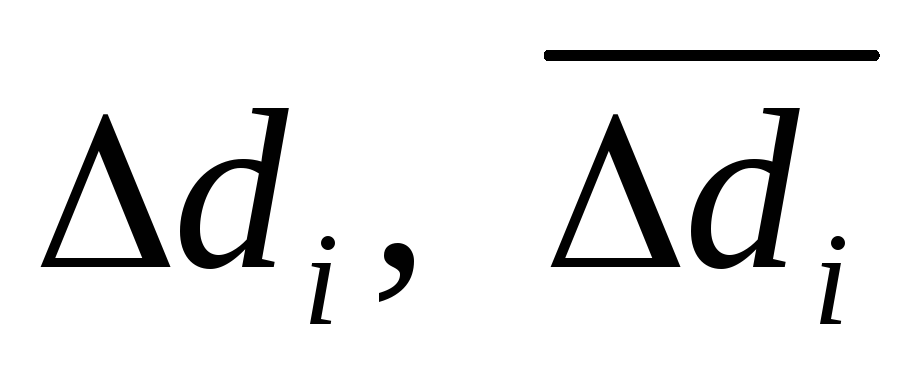 ;
;показатели, базирующиеся на отношениях удельных весов одноименных частей совокупности:
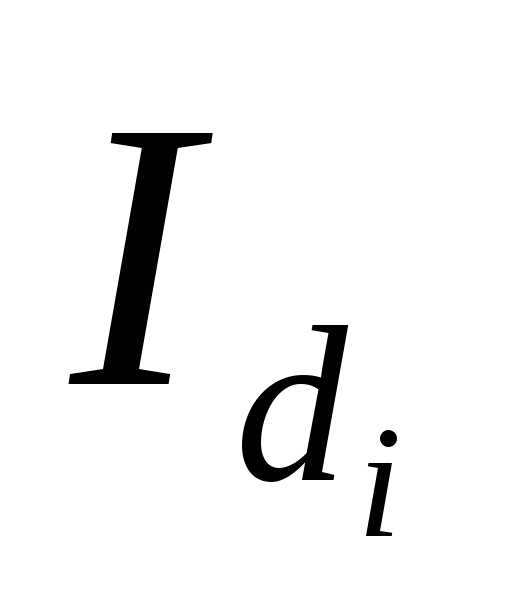 .
.
Задача 7.8 Провести анализ структуры и структурных сдвигов доходов операторов связи за 2007 – 2009 годы и сделать выводы.
Доходы операторов Таблица 7.14
-
Операторы
Доходы, млн. долл. Д
2007
2008
2009
Оператор 1
404
593
678
Оператор 2
651
612
630
Оператор 3
41
59
60
Оператор 4
104
86
132
Итого
1200
1350
1500
Расчетные таблицы
Таблица 7.15
-
Операторы
1. Удельный вес,%
dij = Дij / ΣДij
2. Прирост удельного веса
∆d=dij - dij-1
2007
2008
2009
2008-2007
2009-2008
2009-2007
di1
di2
di3
∆d=di2-di1
∆d=di3-di2
∆d=Idi3-di1I
Оператор 1
33,66
43,93
45,20
10,27
1,27
11,54
Оператор 2
54,25
45,33
42,00
- 8,92
- 3,33
- 12,25
Оператор 3
3,42
4,37
4,00
0,95
- 0,37
0,58
Оператор 4
8,67
6,37
8,80
- 2,30
2,43
0,13
Итого
100
100
100
0
0
0
Таблица 7.16
|
Операторы
|
3. Темпы роста
|
Средне- годовой темп роста | |
|
|
Id = di2/di1 |
Id = di3/di2 |
|
|
Оператор 1 |
1,3047 |
1,0290 |
1,1587 |
|
Оператор 2 |
0,8356 |
0,9265 |
0,8800 |
|
Оператор 3 |
1,2791 |
0,9153 |
1,0820 |
|
Оператор 4 |
0,7350 |
1,3814 |
1,0076 |
|
√ |
1,3047*1,0290 |
|
1,158679 |
|
√ |
0,8356*0,9265 |
|
0,879877 |
|
√ |
1,2791*0,9153 |
|
1,082017 |
|
√ |
0,7350*1,3814 |
1,007635 | |
|
|
по модулю Idi2-di1I
|
(di2-di1)2
|
(di2-i1)2 di1
|
по модулю Idi3-di2I
|
(di3-di2)2
|
(di3-di2)2 di2
|
по модулю Idi3-di1I
|
|
Опер 1 |
10,27 |
105,25 |
3,13 |
1,27 |
1,62 |
0,04 |
11,54 |
|
Опер 2 |
8,92 |
79,51 |
1,46 |
3,33 |
11,11 |
0,25 |
12,25 |
|
Опер 3 |
0,95 |
0,91 |
0,27 |
0,37 |
0,14 |
0,03 |
0,58 |
|
Опер 4 |
2,30 |
5,27 |
0,61 |
2,43 |
5,90 |
0,93 |
0,13 |
|
|
22,44 |
190,94 |
5,47 |
7,40 |
18,77 |
1,24 |
24,50 |
Расчет показателей Таблица 7.18
-
1. Удельные веса, %
dij = Пij *100/
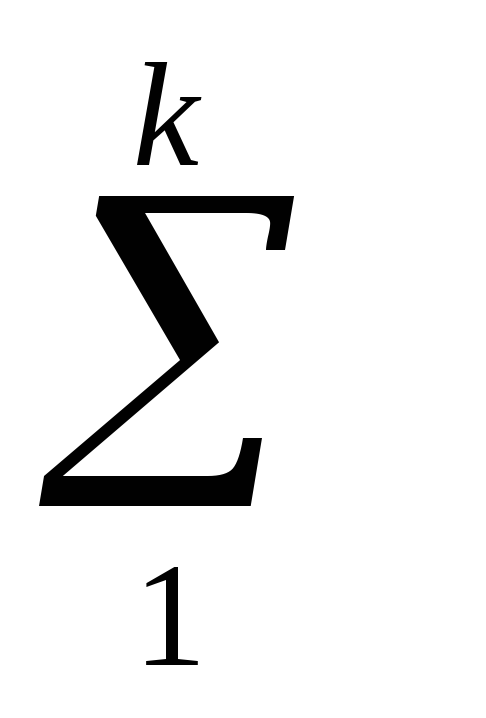 Пij
Пij i – часть совокупности;
j – период времени;
k – количество показателей.
2. Прирост удельного веса (доли)
∆di = d ij – d ij-1;
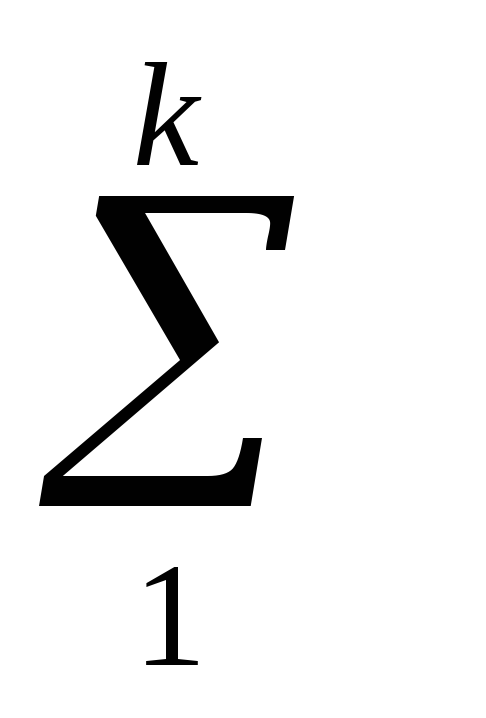 ∆di
= 0
∆di
= 03.Средний «абсолютный» прирост удельного веса
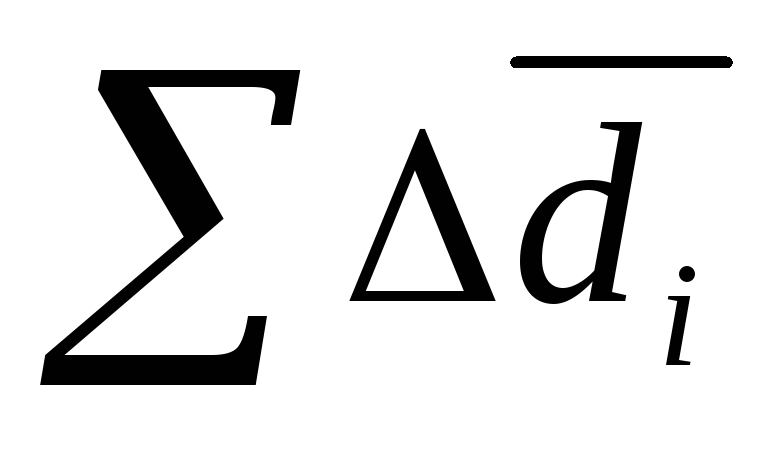 =
=
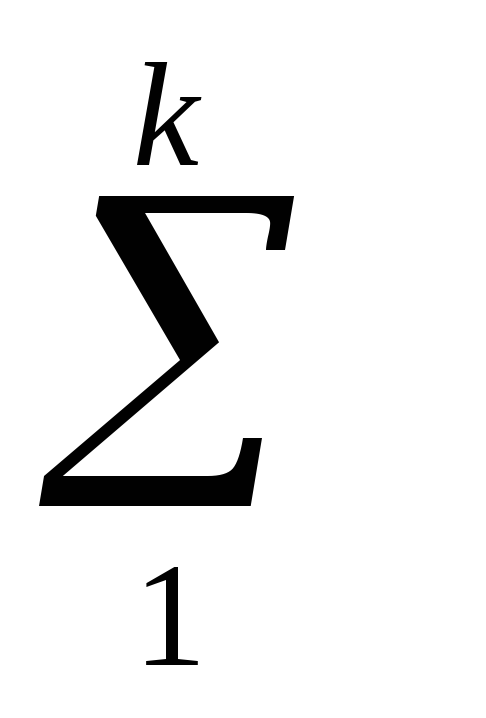 (din-
di1)
/ (n-1)
= 0
(din-
di1)
/ (n-1)
= 04.Темп роста удельного роста
Средний темп роста удельного роста
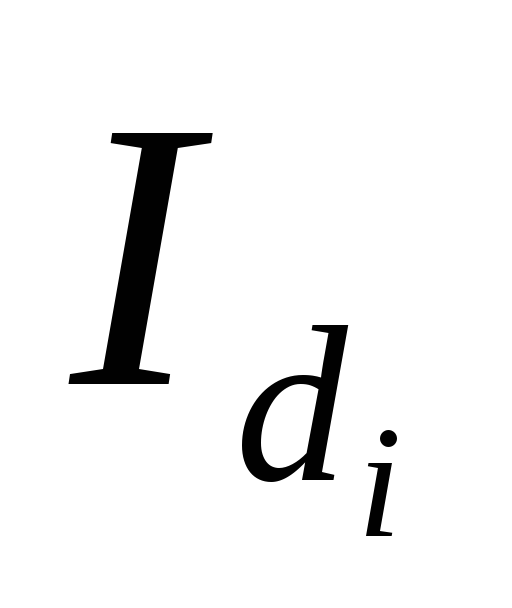 =
dij=dij
/ dij-1
=
dij=dij
/ dij-1 
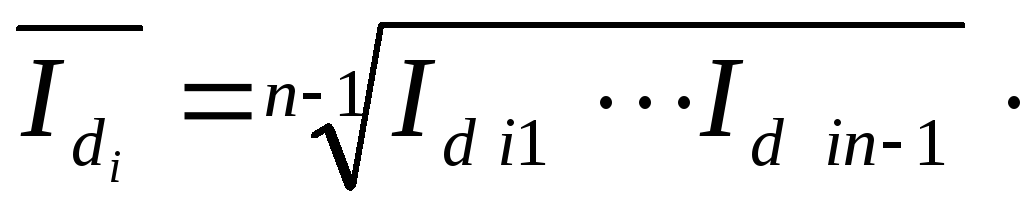
n - количество лет
5. Линейный коэффициент "абсолютных"
структурных сдвигов
 dj-dj-1
= (Σ
|I
dij-dij-1|)/
k
dj-dj-1
= (Σ
|I
dij-dij-1|)/
k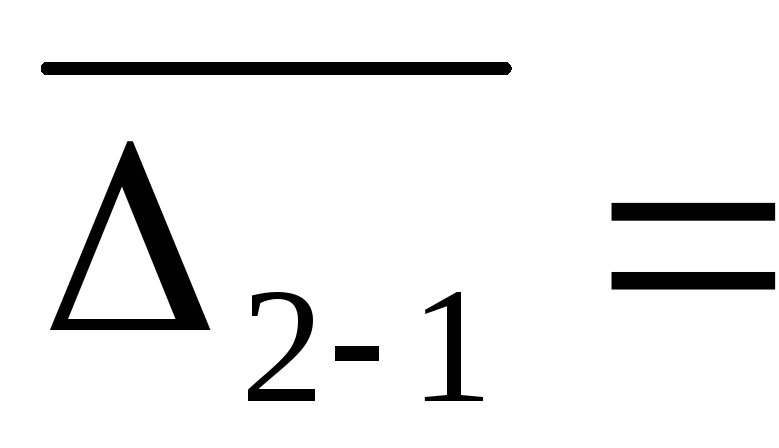 22,44/4
= 5,61 проц. пункт
22,44/4
= 5,61 проц. пункт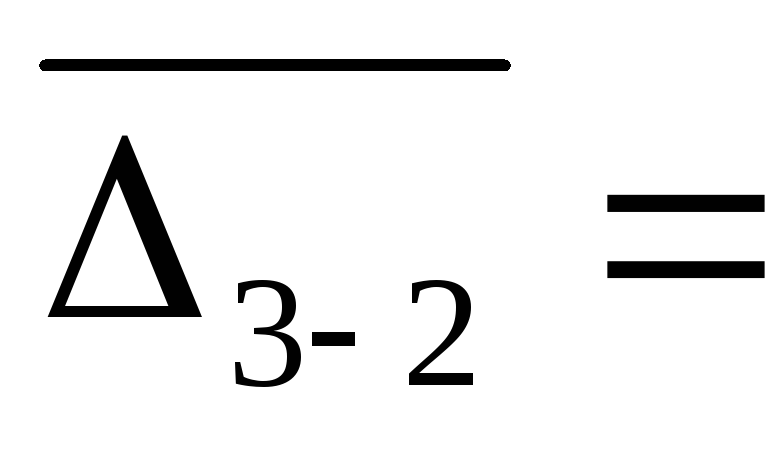 7,40/4
= 1,85 проц. пункт
7,40/4
= 1,85 проц. пункт djn-dij-1
= (Σ
| din-di1|)/
k(n-1)
djn-dij-1
= (Σ
| din-di1|)/
k(n-1)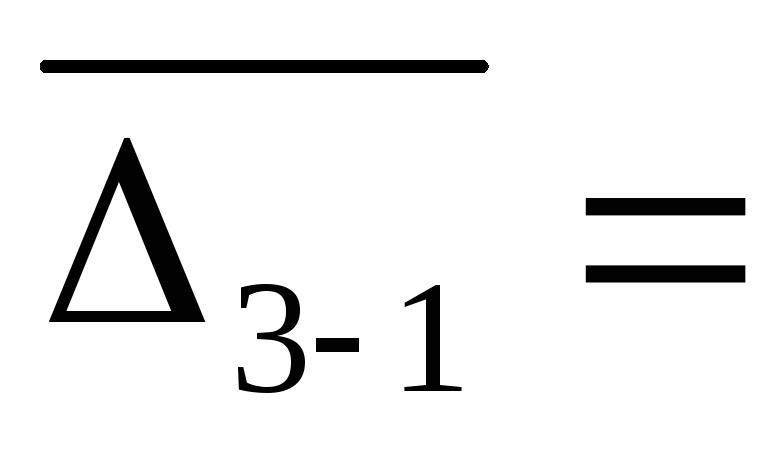 24,50/4/(3-1)
3,06
проц. пункт
24,50/4/(3-1)
3,06
проц. пункт6. Квадратический коэффициент «абсолютных»
структурных сдвигов
σdij-dij-1 =√(Σdij-dij-1)2/k
σd2-d1 =
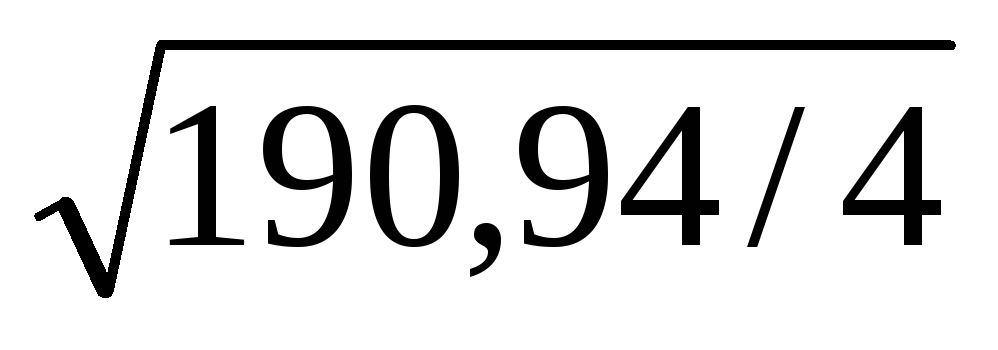 = 6,91 проц. пункт
= 6,91 проц. пунктσd3-d2 =
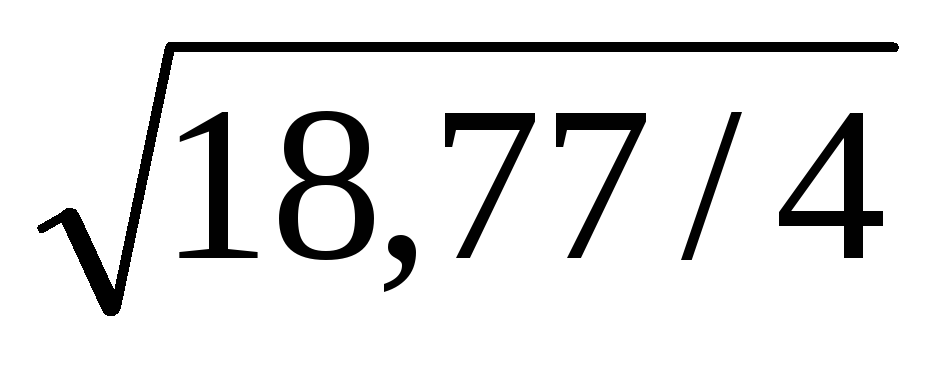 = 2,17 проц. пункт
= 2,17 проц. пункт7. Квадратический коэффициент 'относительных" структурных сдвигов
σdij/dij-1 = √ (Σdij-dij-1)2*100/dij-1
σd2/1 =
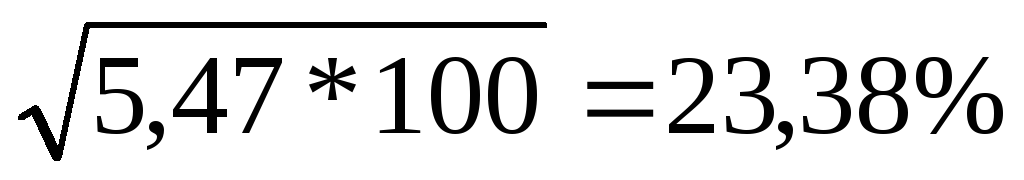
σd3/2 =
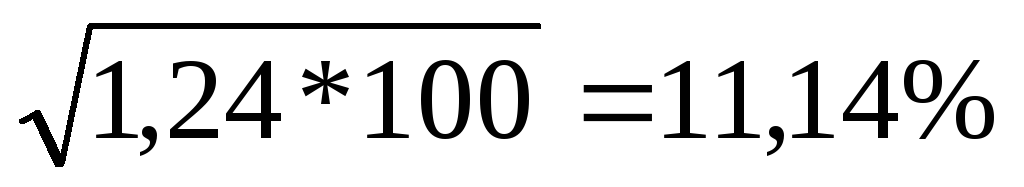
По каждому структурному
показателю структурный «абсолютный»
сдвиг определяется за весь период как:
![]() (din
– di1)
/ (n-1),
а
(din
– di1)
/ (n-1),
а
![]() (din
– di1)
/ (n-1)
= 0.
(din
– di1)
/ (n-1)
= 0.
Для оператора 1: (45,20 - 33,66) / (3 - 1) = 5,770 процентных пункта;
для оператора 2: (42,00 - 54,25) / (3 - 1) = - 6,125 процентных пункта;
для оператора 3: (4,00 - 3,42) / (3 - 1) = 0,290 процентных пункта;
для оператора 4: (8,80 - 8,67) / (3 - 1) = 0,065 процентных пункта.
![]() (din
– di1)
/ (n-1)
= 5,770 – 6,125 + 0,290 + 0,065 = 0.
(din
– di1)
/ (n-1)
= 5,770 – 6,125 + 0,290 + 0,065 = 0.
Выводы:
1. Удельный вес доходов оператора 1 ежегодно растет, а оператора 2 – падает, у операторов 3 и 4 наблюдается сначала падение, затем рост. Темпы роста подтверждают вышеприведенные выводы.
2. Линейный коэффициент "абсолютных" структурных сдвигов показывает, что удельный вес доходов в среднем за 2008 год изменился на 5,61, за 2009 год – на 1,85 и за 2009 год по сравнению с 2007 годом – на 3,06 процентных пункта. Снижение средней величины удельного веса доходов с 5,61 до 1,85 свидетельствует о начале стабилизации на анализируемых объектах и оценивается положительно.
3. Квадратический коэффициент «абсолютных» структурных сдвигов подтверждает ранее сделанный вывод: удельный вес отдельных частей совокупности (доходов операторов) изменился за 2008 год на 6,91, за 2009 год – на 2,17 процентных пункта.
4. Квадратический коэффициент 'относительных" структурных сдвигов показывает, что если за 2008 год вес доходов каждого оператора в среднем изменился на 23,38% своей величины, то за 2009 год – на 11,14%.
5. Сводную оценку изменения
за 2007-2009 годы дает средний линейный
коэффициент "абсолютных" структурных
сдвигов
![]() 3,06 проц. пункта, что свидетельствует
о достаточно равномерном влиянии
факторов на доходы операторов.
3,06 проц. пункта, что свидетельствует
о достаточно равномерном влиянии
факторов на доходы операторов.
6. По отдельной части совокупности (доходы операторов) структурный абсолютный сдвиг за весь период изменялся ежегодно на процентных пункта:
оператора 1: 5,770 (увеличение); оператора 2: - 6,125 (уменьшение);
оператора 3: 0,290 (увеличение): оператора 4: 0,065 (увеличение).
Общая сумма средних ежегодных изменений равна 0.
5,770 - 6,125 + 0,290 + 0,065 = 0
