6.2 Корреляционно-регрессионный анализ для многофакторной модели.

Задача 5.3 По данным о доходах основной деятельности, внереализационных доходов и прибыли (млрд. руб.) построить уравнение связи, измерить тесноту связи между прибылью и доходами, провести полный корреляционно- регрессионный анализ связи.

Исходные данные и расчеты Таблица 6.3

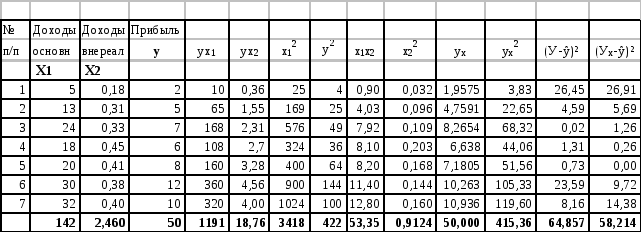
1. Выбор формы уравнения множественной регрессии.

Линейная функция: a₀ + a₁x₁ + a₂x₂;

2. Параметры уравнения множественной регрессии.

Параметры уравнения множественной регрессии рассчитываются методом наименьших квадратов на основе решения системы нормальных уравнений.

a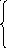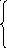₀n + a₁x₁+ a₂x₂=y, 7a₀+142a₁+ 2,46a₂= 50,

a₀x₁+ a₁x²₁+ a₂x₁x₂=yx₁, 142a₀+ 3418a₁+ 53,35a₂= 1191,

a₀x₂+ a₁x₁x₂+ a₂x²₂=yx₂. 2,46a₀+53,35a₁+ 0,9124a₂= 18,76.

а₀ = 0,0086; а₁ = 0,3148; а₂ = 2,1783. -0,0086+ 0,3148x₁ + 2,1783x₂

Расчеты показали, что с увеличением доходов от основной деятельности на 1 млрд. руб. прибыль увеличится в среднем на 314,8 млн. руб., а с увеличением внереализационных доходов на 1 млрд. руб. прибыль увеличится в среднем на 2,18 млрд. руб.

3. Расчет множественного коэффициента корреляции

Множественный коэффициент корреляции определяется по формуле:

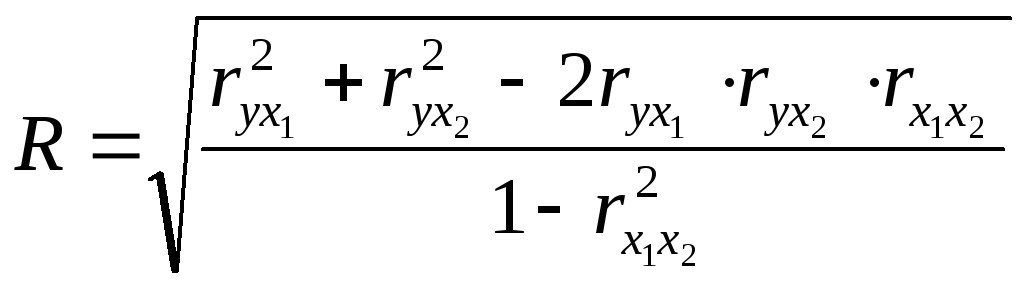
= 0,9475

4. Частные (парные) коэффициенты корреляции

Частные (парные) коэффициенты корреляции определяются по формуле:

= = 0,94653;

= = 0,67617;

= = 0,68117.

5. Строится корреляционная матрица переменных: у, х₁, х₂.

Корреляционная матрица переменных: у, х₁, х₂.

	х1	х2	у
х1	1,0	0,68117	0,94653
х2	0,68117	1,0	0,67617
у	0,94653	0,67617	1,0

Наибольшее влияние на прибыль (у) оказывают доходов от основной деятельности (х₁).

6. Частные коэффициенты эластичности.

; .

Расчеты показали, что с увеличением доходов от основной деятельности на 1%. прибыль в среднем увеличивается на 0,894%, а с увеличением доходов от внереализационной деятельности на 1% прибыль увеличивается в среднем на 0,1072 %.

7. Проверка значимости коэффициента множественной корреляции по критерию Фишера-Снедекора.

При F_р > F_кр коэффициент множественной корреляции значимый.

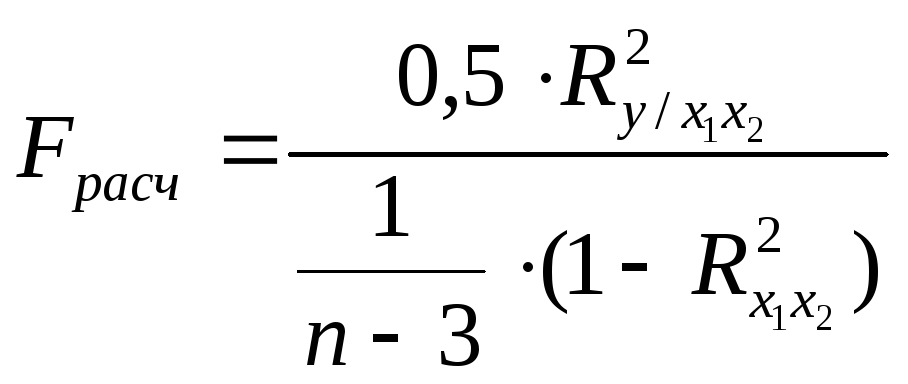
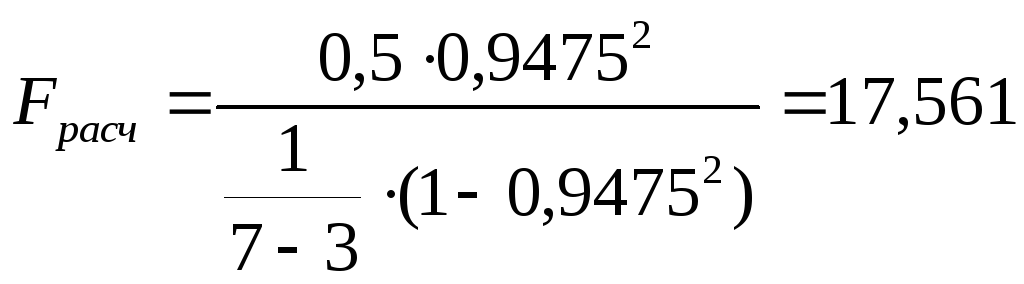
F_кр при равен 6,94.

17,561 > 6,94, значит коэффициент множественной корреляции значимый.

8. Расчет β-коэффициентов

β-коэффициент определяется по формуле:

= 0,3148*8,7622/3,0438 = 0,9062; = 2,1783*0,0826/3,0438 = 0,0591

₁ показывает, что на 0,9062 среднего квадратического отклонения σу изменяется результативный признак у при изменении фактора х₁ на величину его среднего квадратического отклонения σх₁, и на 0,0591 среднего квадратического отклонения σу изменяется результативный признак у при изменении фактора х₂ на величину его среднего квадратического отклонения σх₂. Влияние фактора х₁ более сильное.

9. Частные коэффициенты детерминации.

= 0,94653*0,9062 = 0,85775; = 0,67617*0,0591 = 0,03996.

Расчеты показали, что на 85,78 % вариация прибыли объясняется вариацией доходов от основной деятельности, на 4,0 % вариацией доходов от внереализационной деятельности, 10,24 % - влияние не учтенных моделью факторов.

10. Множественной коэффициент детерминации.

Таким образом, моделью учтено влияние 89,78 % факторов.

11. - коэффициенты

- коэффициенты показывают влияние каждого учтенного моделью фактора.

;

.

Наибольшее влияние на прибыль оказывает фактор х₁ - доходы от основной деятельности.

12. Измерение тесноты связи через корреляционное отношение эмпирических и теоретических значений (у).

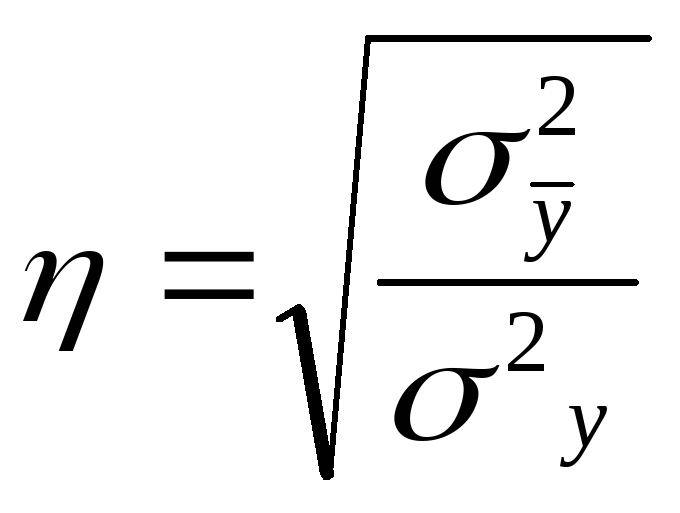
Связь прямая, сильная.

Используется при любой форме связи, прямолинейной и криволинейной.

13. Оценка значимости факторов для включения в модель.

для фактора х₁:

;

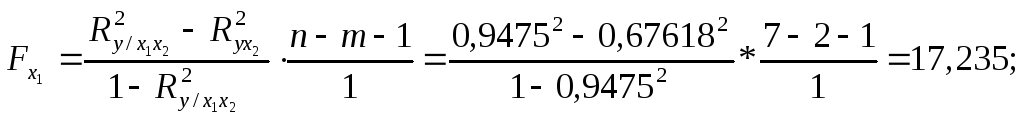для фактора х₂:

.

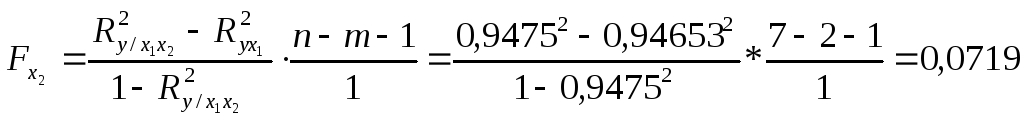При F_р > F_кр коэффициент множественной корреляции значимый.

F_кр при равен 6,94.

- степени свободы; - число параметров уравнения;

- число наблюдений.

F_кр - Таблица «Значения F- критерия Фишера при уровне значимости 0,05»

Вывод: - для фактора х₁ F_р > F_кр (17,235 > 6,94), коэффициент множественной корреляции значимый.

- для фактора х₂ F_р < F_кр (0,0719 < 6,94), коэффициент множественной корреляции незначимый, можно в модель не включать.

14. Оценка значимости уравнения.

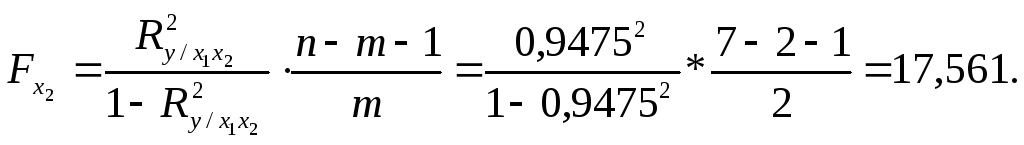
для уравнения F_р > F_кр, - уравнение значимо.

Задача 6.4 Определить тесноту связи между прибылью, среднегодовой стоимостью основных производственных фондов и затратами на 100 руб. продукции с помощью коэффициента конкордации.

Исходные данные и расчеты Таблица 5.4

№№ п/п	Прибыль,   млн. руб.	Стоимость ОПФ млн. руб.	Затраты на 100 руб., руб.	Ранжирование факторов			Сумма рангов m	Квадраты сумм рангов m
	Y	X	Z	Ry	Rx	Rz	∑Ri	(∑Ri)²
1	300	4,1	73	1	2	3	6	36
2	950	6,6	80	4	5	5	14	196
3	480	3,9	67	2	1	1	4	16
4	520	4,2	75	3	3	4	10	100
5	1000	6,3	72	5	4	2	11	121
∑							45	469

Коэффициент конкордацииW :

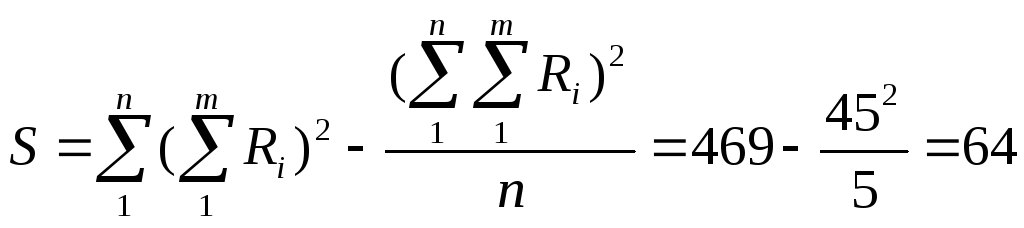
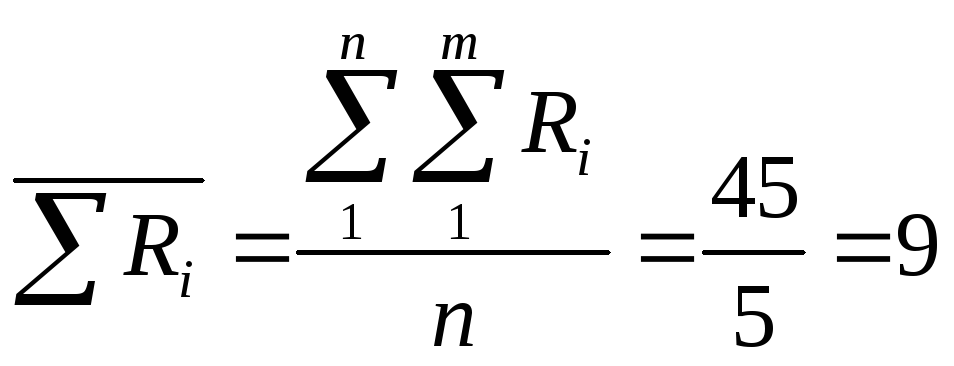
или S = (6-9)²+(14-9)²+(4-9)²+(10-9)²+(11-9)² = 64

Связь между приведенными показателями (факторами) сильная, прямая.