Курсовая_интегралы_2(2015)

, где контур треугольника , , .

8. Проверить, является ли данное выражение полным дифференциалом. Если да, то найти .

Вариант 11

1. Расставить пределы интегрирования двумя способами в двойном интеграле

в декартовых координатах для области

2. Вычислить двойной интеграл:

3. Вычислить двойной интеграл:

4. Вычислить тройной интеграл:

5. Найти площадь области, ограниченной кривыми:

6. Найти объем тела, ограниченного поверхностями: , ,

, .

7. Вычислить непосредственно и с помощью формулы Грина: , где квадрат ,,,.

8. Проверить, является ли данное выражение полным дифференциалом. Если да, то найти .

Вариант 12

1. Расставить пределы интегрирования двумя способами в двойном интеграле

в декартовых координатах для области

2. Вычислить двойной интеграл: ,.

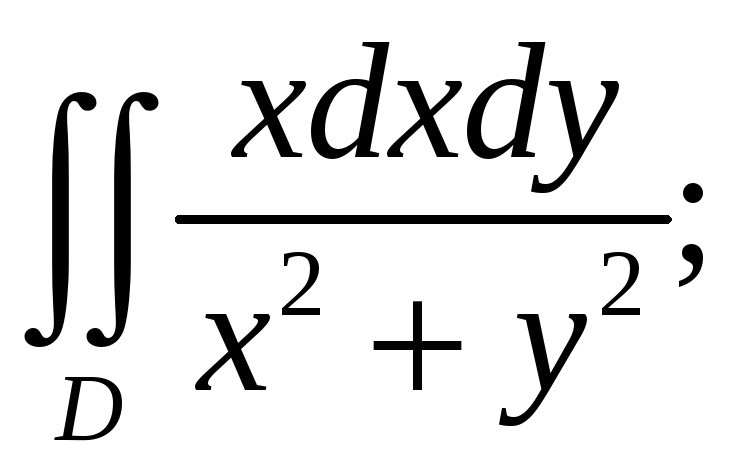
3. Вычислить двойной интеграл:

4. Вычислить тройной интеграл: .

5. Найти площадь области, ограниченной кривыми:

6. Найти объем тела, ограниченного поверхностями: , , ,

, .

7. Вычислить непосредственно и с помощью формулы Грина: , где парабола и хорда .

8. Проверить, является ли данное выражение полным дифференциалом. Если да, то найти .

Вариант 13

1.Расставить пределы интегрирования двумя способами в двойном интеграле

в декартовых координатах для области

2. Вычислить двойной интеграл:

3. Вычислить двойной интеграл:

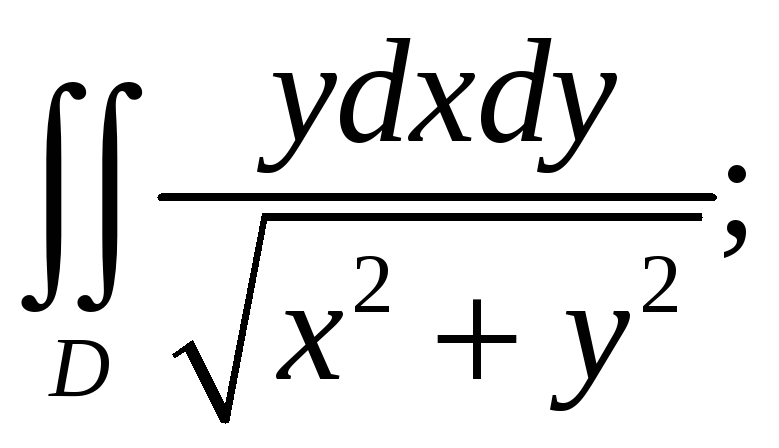
4. Вычислить тройной интеграл: .

5. Найти площадь области, ограниченной кривыми: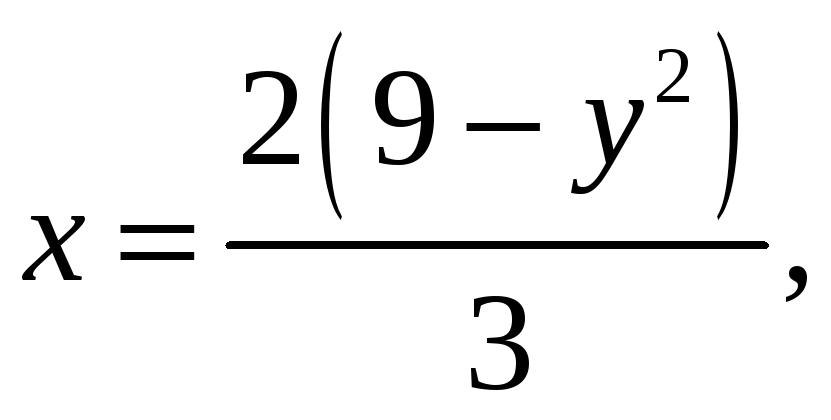

6. Найти объем тела, ограниченного поверхностями: , , ,

, .

7. Вычислить непосредственно и с помощью формулы Грина: , где окружность .

8. Проверить, является ли данное выражение полным дифференциалом. Если да, то найти .

Вариант 14

1.Расставить пределы интегрирования двумя способами в двойном интеграле

в декартовых координатах для области

2. Вычислить двойной интеграл:

3. Вычислить двойной интеграл: .

4. Вычислить тройной интеграл: .

5. Найти площадь области, ограниченной кривыми:

6. Найти объем тела, ограниченного поверхностями: , , ,

, .

7. Вычислить непосредственно и с помощью формулы Грина:

, где контур треугольника , , .

8. Проверить, является ли данное выражение полным дифференциалом. Если да, то найти .

Вариант 15

1.Расставить пределы интегрирования двумя способами в двойном интеграле

в декартовых координатах для области

2. Вычислить двойной интеграл:

3. Вычислить двойной интеграл:

4. Вычислить тройной интеграл:

5. Найти площадь области, ограниченной кривыми:

6. Найти объем тела, ограниченного поверхностями: , , ,

.

7. Вычислить непосредственно и с помощью формулы Грина:

, где контур прямоугольника , .

8. Проверить, является ли данное выражение полным дифференциалом. Если да, то найти .

Вариант 16

1.Расставить пределы интегрирования двумя способами в двойном интеграле

в декартовых координатах для области ,.

2. Вычислить двойной интеграл:

3. Вычислить двойной интеграл:

4. Вычислить тройной интеграл:

5. Найти площадь области, ограниченной кривыми:

6. Найти объем тела, ограниченного поверхностями: , , ,

, .

7. Вычислить непосредственно и с помощью формулы Грина:

, где эллипс .

8. Проверить, является ли данное выражение полным дифференциалом. Если да, то найти .

Вариант 17

1.Расставить пределы интегрирования двумя способами в двойном интеграле

в декартовых координатах для области

2. Вычислить двойной интеграл:

3. Вычислить двойной интеграл:

4. Вычислить тройной интеграл:

5. Найти площадь области, ограниченной кривыми:

6. Найти объем тела, ограниченного поверхностями: , , ,

.

7. Вычислить непосредственно и с помощью формулы Грина:

, где контур прямоугольника , .

8. Проверить, является ли данное выражение 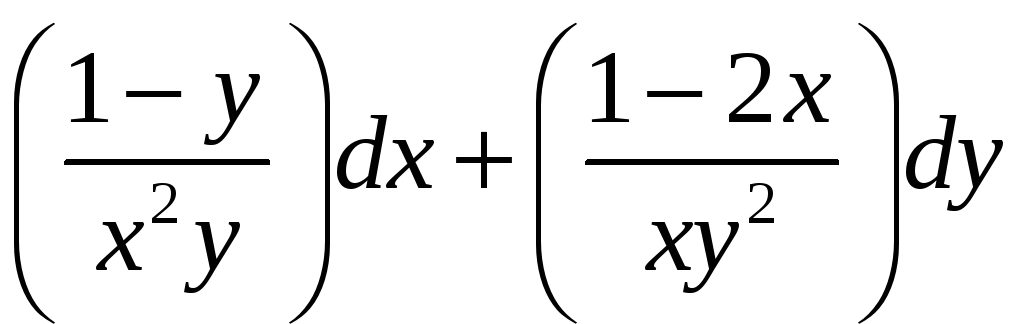полным дифференциалом. Если да, то найти .

Вариант 18

1.Расставить пределы интегрирования двумя способами в двойном интеграле

в декартовых координатах для области

2. Вычислить двойной интеграл:

3. Вычислить двойной интеграл: и полярной осью.

4. Вычислить тройной интеграл:

5. Найти площадь области, ограниченной кривыми:

6. Найти объем тела, ограниченного поверхностями: , , ,

, .

7. Вычислить непосредственно и с помощью формулы Грина: , где контур треугольника

,,.

8. Проверить, является ли данное выражение полным дифференциалом. Если да, то найти .

Вариант 19

1.Расставить пределы интегрирования двумя способами в двойном интеграле

в декартовых координатах для области

2. Вычислить двойной интеграл:

3. Вычислить двойной интеграл: и полярной

осью.

4. Вычислить тройной интеграл:

5. Найти площадь области, ограниченной кривыми:

6. Найти объем тела, ограниченного поверхностями: ,

, , , .

7. Вычислить непосредственно и с помощью формулы Грина: , где контур прямоугольника , .

8. Проверить, является ли данное выражение полным дифференциалом. Если да, то найти .

Вариант 20

1.Расставить пределы интегрирования двумя способами в двойном интеграле

в декартовых координатах для области

2. Вычислить двойной интеграл:

3. Вычислить двойной интеграл:

4. Вычислить тройной интеграл:

5. Найти площадь области, ограниченной кривыми:

6. Найти объем тела, ограниченного поверхностями: , ,

, , .

7. Вычислить непосредственно и с помощью формулы Грина:

, где контур прямоугольника , .

8. Проверить, является ли данное выражение полным дифференциалом. Если да, то найти .